エクセルによる散布図の書き方、作り方およびテンプレートについて図解入れで解説しています。
おもな内容は下記のとおりです。
・散布図 相関係数 求め方
・散布図 近似曲線 傾き、数式
・散布図 エクセル 色分け
・散布図 行列 見方
・散布図 Webアプリ
業務での統計解析での参考になれば幸いです。(*^_^*)
動画 エクセルで散布図を作成する
Excelで散布図を作成する方法を解説している動画の紹介。
散布図とは？
対応すると推測される２種類のデーターが本当に関係があるかどうかを難解な統計計算を使用しないで図だけで調べるためQC手法のひとつ。
具体的には対応する２種類のデーターを横軸、縦軸にとって打点して作った図のことをいいます。
英語：scatter diagram ,Scatter plot
中国語：散点图
対応する２種類のデーターの事例
1)特性（結果）と要因（原因）の関係
2)ある特性（結果）と他の特性（結果）との関係
3)ある特性（結果）に対する２つの要因（原因）どうしの関係
関連記事：QC七つ道具
エクセル 散布図 フリー
下記にエクセルで作成した散布図があります、ご自由にダウンロードしてご使用ください。
散布図の作り方 書き方 基本
そのつくり方は、次のようにします。
散布図 データー収集
関係があるかどうか調べたい、対のデータを30個以上集める
横軸と縦軸｜折れ線グラフ
二つの項目を横軸と縦軸に取る。このとき、横軸は右にいくほど大きな値を、縦軸は上にいくほど大きな値とするとともに、両軸の目盛幅を同じ幅にする。
二つの項目に原因と結果の関係がある場合は、横軸に原因系を、縦軸に結果系を取る。
プロット図に打点｜XYグラフ
一対のデータをグラフに打点する。
同じデータがある場合は、前に打点した点を○で囲むか、または接近したところに打点する
最後に標題、調査日、サンプル数、作成者などを記入する。
基本的な散布図の見方と活用の仕方
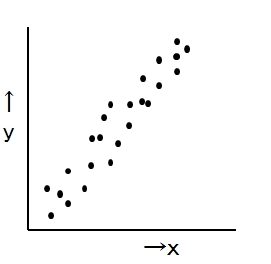
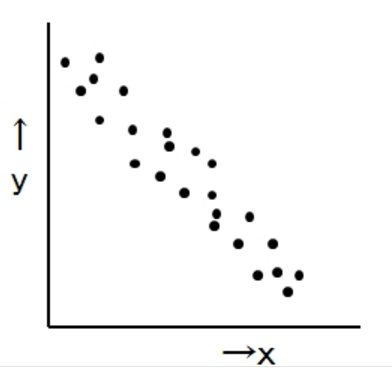
散布図のパターンには、図Ａのように、横軸の増加に伴い縦軸も増加する「正の相関」と、図Ｂのように、横軸の増加に伴い縦軸が減少する「負の相関」とがあります。
また、図Ｃのように、横軸が増加しても縦軸が増加も減少もしないものは、「無相関」といいます。
図Ａおよび図Ｂのように相関がある場合は、横軸または縦軸の項目を管理することによって、縦軸または横軸を管理することができます。
打点の幅が大きくバラツキが大きい場合は、横軸または縦軸の管理精度を上げることによって、バラツキを小さくすることができます。また飛び離れたものがある場合には、その原因を調べて是正処置を行ないましょう。
相関があると考えられるデータであるにもかかわらず無相関となった場合には、条件が異なったデータが混入していることが考えられます。データを層別し、もう一度、散布図を作成することが必要です。
エクセル 散布図の作成
散布図データーの採取
上記の散布図 エクセルファイルを基に散布図を説明します。
調査したい２種類のデーターを対応する形で集めます。
対応するデーターをそれぞれ変数ｘ、ｙとする。
例では下面（X)と上面（Y)の端振れ測定値をサンプルデーターとしています。
データーが少ないと正確な判断ができなくなるので３０組以上のデーターを集めること。
散布図データー選択｜エクセル 散布図 ２軸
散布図データーの範囲を設定してから散布図グラフを選び、散布図。
手順は下記のとおりです。
下面（X)と上面（Y)の端振れのデーターを選択します。
散布図挿入｜エクセル XYグラフ
挿入タグ選択→散布図（X,Y)の挿入を選択します。
散布図の決定
下図のように色々な散布図が表示されるので必要な散布図を選択します。
散布図の自動作成｜エクセル プロット
散布図を選択すると自動的に散布図が作成、描かれます。
但し、サイズおよび表示項目がマッチしていないので修正が必要です。
軸ラベルの設定の変更
散布図グラフの枠を選択し、グラフ要素を表示させます。
次に軸ラベルをチェックを入れると、軸ラベルが表示されるのでX変数、Y変数に適合する
ラベルを入力します。
例ではX変数には下面振れ、Y変数には上面振れと修正します。
エクセル 散布図の完成
サイズ、タイトル等の修正を行い、エクセル 散布図の完成です。
エクセル 散布図の近似曲線の求め方｜回帰直線
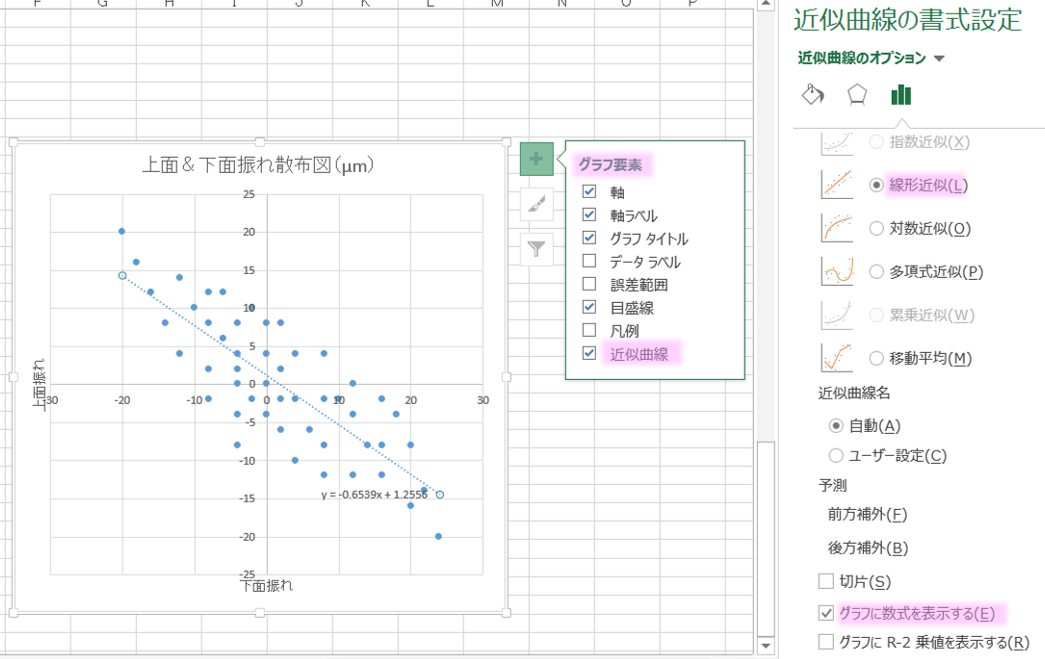
エクセルで散布図の近似曲線を求めたいときは下記のようにします。
１）グラフを選択し、グラフ要素を表示させます。
２）次に近似曲線にチェツクを入れます。
３）近似曲線の書式設定が表示されるので「線形近似」を選択します。
４）グラフに数式を表示させたい場合は「グラフに数式を表示する」を選択します。
＊回帰直線とは、散布図において、予定値を求める際に用いられる直線のことである。2組のデータの中心的な分布傾向を表すもの、予測する際に用いられる。
エクセル 散布図の相関係数の求め方
次に相関係数を求めます。
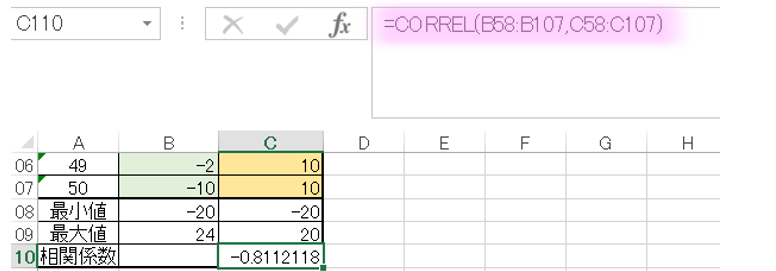
シートの空いているところ（ここではセルC110）に「相関係数」を作成します。
下記のようなCORREL関数の数式を入力します。
=CORREL(B58:B107,C58:C107)
『B58:B10』はX変数データー入力範囲
『C58:C107』はY変数データー入力範囲
セルC11０に相関係数 －0.8112118が計算、表示されます。
X変数、Y変数がともに数量（間隔尺度・比尺度）であり、直線的関係が見られる場合は、ピアソンの積率相関係数（単相関係数）を用います。この例でも変数はともに数量（間隔尺度）ですからピアソンの積率相関係数（単相関係数）を求めることができます。
CORREL関数 説明：
CORREL関数は指定した二つの配列の相関係数を返す事で二つの配列の相関関係を調べる事ができます。
引数の指定方法：
配列1 数値を含む名前、配列、セル範囲の参照を指定
配列2 もう一方のデータが入力されているセル範囲、数値を含む名前や配列を指定
C2セルに =CORREL(A2:A4,B2:B4)を入力すると以下の表の結果となります。
C2セルの=CORREL(A2:A4,B2:B4)では収益の行のA2：A4を参照し、B2：B4は来店者数を参照しています。
そして、CORREL関数によって利益と生産数の相関関係を表す相関係数0.9958がC2セルに出力されます。
（小数点第四位まで表示）
| A | B | C | |
| 1 | 利益 | 生産数 | 相関係数 |
| 2 | 50000 | 120 | 0.9958 |
| 3 | 60000 | 130 | |
| 4 | 30000 | 90 |
散布図の相関係数 グラフの見方
相関係数による相関関係の強弱の判断基準は下記のとうりである。
0.8 ≦｜ ｒ ｜ → 強い相関あり
0.6 ≦｜ ｒ ｜ ＜0.8 → 相関あり
0.4 ≦｜ ｒ ｜ ＜0.6 → 弱い相関あり
｜ ｒ ｜＜0.4 → ほとんど相関なし
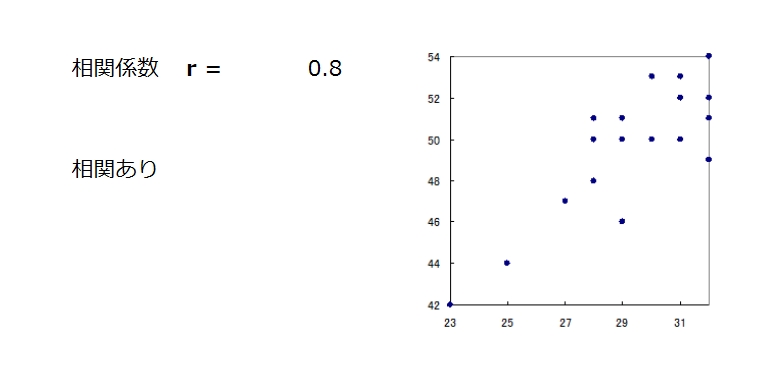
色々な散布図の見方
正の相関があり
ｘが増えるとｙも増えていく傾向があるので”正の相関がある”といえる。Ｘを正しく管理すればｙも管理することができる。
負の相関があり
ｘが増えるとｙが減少する傾向があるので”負の相関が
ある”といえる。Ｘを正しく管理すればｙも管理することが
できる。
正の相関がありそう
ｘが増えると傾向的にｙも増えているように見えるので”正の相関があるそうだ”といえる。
但し点の並びが直線的でないのはｙの値がｘ以外にも影響を受けていると推測されます。
ｘ以外の要因についても調査することが必要です。
負の相関がありそうだ
ｘが増えると傾向的にｙも減少しているように見えるので”負の相関があるそうだ”といえる。
但し点の並びが直線的でないのはｙの値がｘ以外にも影響を受けていると推測されます。
ｘ以外の要因についても調査することが必要です。
相関がない
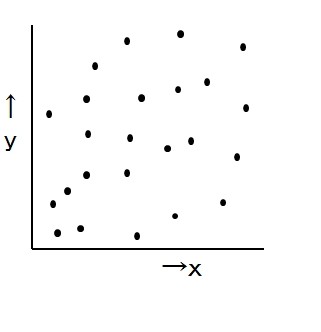
ｘが増えがない”と いいます。ｘ以外のｙに影響する要因を見つけることが大切です。
散布図を見るときの注意事項
異常点がないか？
全体のならびから異常に飛び離れている点があればその原因を調べること。多くの場合測定誤り、不良品混入などの特別な原因なのでその際はそのデーターを省くこと。
層別の有無
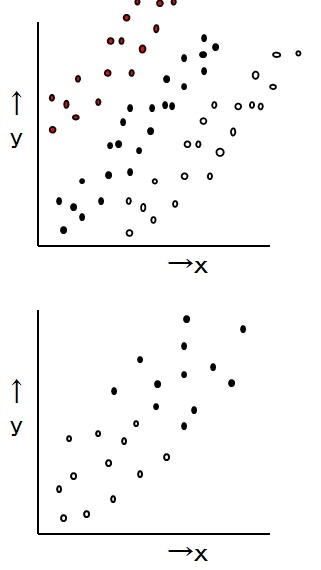
全体としてみると相関がないようだが層別すると相関がある場合や逆に相関がありそうだが層別すると相関がない場合があるので散布図を作成する前に層別について検討し点の色を変更するとか印を変更（○、●）する必要があります。
統計学の相関係数
２つのデーターの間に相関関係があるかどうかを数値的に判断するには相関係数と呼ばれる指標を利用する。
変数x, yのデータがn組あるとき、つまり(X1,Y1)(X2,Y2)・・・・（Xn,Yn)相関係数は下記の式で表せる。
＊つまり、相関係数は共分散SxyをXの標準偏差SxとYの標準偏差Sｙで割ったものである。
相関係数は通常ｒと言う記号で表示されー１から１までの値をとる。
-1 ≦ ｒ ≦ +１
Excelで相関係数を計算するには、correl という関数を使 =correl(範囲１,範囲２)
相関係数は対になっている量に対して与えられるもので、範囲１と範囲２は並んでいなけれなりません。
相関に関する検定と推定
サンプルから求めたｒは試料相関係数であって母集団の相関係数ρと一致するわけではない。
そこで母集団の相関の有無を正しく判断するために試料相関係数ｒの有意性の検定を行うことが必要になってくる。
相関に関する検定（無相関の検定）
1)仮説の設定
・帰無仮説 Ho： 母相関係数 ρ =0
・対立仮説 H1： 母相関係数 ρ≠0
2)検定統計量ｔの計算
・データーから相関係数ｒを計算する。
・相関係数ｒの自由度φを求める。
データーの対の数をｎとすると
φ＝ｎ－２
・相関係数ｒとｎより検定統計量ｔを算出する。
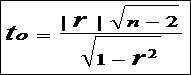
3）有意確率Ｐを求める
検定統計量ｔから有意確率Ｐ（％）を求める
ｔ分布表もしくはＥｘｃｅｌ関数（ＴＤＩＳＴ）を使用する。
4）帰無仮説の判定をする。
有意確率Ｐ（％）と有意水準α（％）の比較をし判定を下す
Ｐ（％）＞α（％ →採択 『母相関係数ρ＝０と相関係数ｒの差がない』
Ｐ（％）≦α（％ →不採 『母相関係数ρ＝０と相関係数ｒの差がある』
ｔ分布
有意確率Ｐを求める
相関に関する検定と推定（具体事例）
Ｅｘｅｒｃｉｓｅ１：
サンプル組数が24、相関係数が0.476の時、母相関係数が０であるか
を検定てください。
＜仮説の設定＞
・帰無仮説 Ho： 母相関係数 ρ =0
・対立仮説 H1： 母相関係数 ρ≠0
＜計算＞
相関係数ｒ 0.48
サンプル組数 24
自由度 22
検定統計量to 2.54 ← 計算式'(ABS(ｒ)*SQRT(ｎ-2))/SQRT(1-ｒ*ｒ）
有意確率P ### ← ＴＤＩＳＴ(to ＊両側検定
＜判定： Ｐ＝1.87％ α（％）＝5％
∴P≦α
→不採択 『母相関係数ρ＝０と相関係数ｒの差がある』
つまり有意水準５％で有意差がある。
＜説明＞
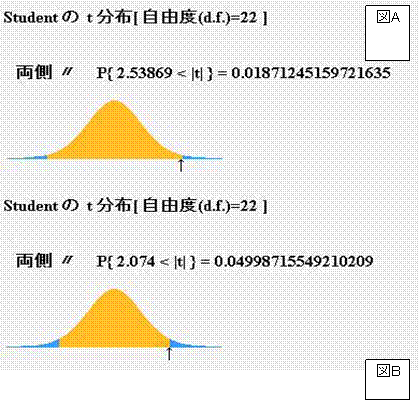
相関係数ｒ 0.476 自由度φ＝２２のときの検定統計量toは2.53869であるから図Aのようなｔ分布となる。（両側確率：１．８７％）
一方、図Bは検定統計量toは2.538689の時のｔ分布である（両側確率：５％）
母相関係数ρがゼロの場合でも、相関係数ｒは-1から1の間でばらつくがB図のように有意水準を５％として信頼区間を表現すると黄色部分が９５％の信頼区間となりこの範囲に入れば帰無仮説 Ho： 母相関係数 ρ =0 は採択される。
けれども例題の場合は９５％の信頼区間の外にあるために仮説は破棄される。
但し有意水準を１％とした場合は採択される。
相関に関する検定と推定
母相関係数の区間推定
1)相関係数ｒをZ変換した値Z（フィシャーのZ変換）をｚ変換図表もしくは’Excel関数FISHERを用いて求める。
2)母相関係数をZ変換した値ξ（フィシャーのZ変換）の信頼度９５％の信頼限界を次式より求める
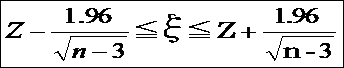
3）ξの信頼限界を逆変換して母相関係数の信頼限界を求める。
＊ｚ変換図表もしくは’Excel関数FISHERINVを用いて求める。
参考文献：ＱＳＳ－普通科テキスト 統計的手法 日本規格協会
オンラインWEB 散布図アプリ
散布図 アプリはソフトウェアをダウンロードしたりインストールしたりする必要はありません。いつでもどこでもデザインやグラフを作成したりアクセスしたりすることができます。必要なのは、インターネット接続とパソコンだけです、外出先でも常に作成することができます。
Googleドライブ スプレッドシート 散布図
エクセルを使う方法で、手軽に散布図が作れます。
グラフをホームページやブログに埋め込んでインターネットに公開することもできます。
方法はGoogleスプレッドシートでグラフ表示用のHTMLコードを生成し、ホームページやブログのHTMLの中に手動で埋め込みます。
下記がGoogleスプレッドシートで作成した散布図を埋め込んだサンプルです。
関連サイト：GoogleスプレッドシートのグラフをWebで公開する方法
Microsoft Excel Online
オンラインで使用できるExcelです。
作成できるグラフは、縦棒グラフ、線グラフ、円グラフ、横棒グラフ、面グラフ、散布図、レーダーチャートなどです。
Excel Onlineの場合、グラフのみを保存する機能はない、グラフを画像として保存するには、キャプチャツールなどで取り込んで切り抜く必要があり。
Canva グラフメーカー 散布図 アプリ
Canvaは、オーストラリアのスタートアップ企業が提供する、ブラウザベースのデザイン作成ツールです。写真コラージュやプレゼン、ソーシャルメディア投稿など様々な用途に合わせテンプレートが用意されており、ツール内の素材をドラッグ＆ドロップで入れ込むだけで完成します。
Canvaのグラフメーカーはグラフ・図の無料オンライン作成ソフト で時間もかからず、数分で美しいグラフや図を作成できます。生データが視覚的に分かりやすく容易に理解できる形に変わります。
Canvaでは、出来上がりのイメージ（グラフの種類）を選んで、数値を入力するだけで、グラフを簡単に作成できます。
散布図も作成できます。
グラフをGoogleスプレッドシートと同様にホームページやブログに埋め込んでインターネットに公開することもできます。
下記がCanva グラフメーカーで作成した散布図を埋め込んだサンプルです。
散布図 英語版 説明
散布図は英語では”scatter diagram”と呼びます。
What is a Scatter Diagram？
Also called: scatter plot, X-Y graph
The scatter diagram graphs pairs of numerical data, with one variable on each axis, to look for a relationship between them. If the variables are correlated, the points will fall along a line or curve. The better the correlation, the tighter the points will hug the line. This cause analysis tool is considered one of the seven basic quality tools.
Referenced from：what is a Scatter Diagram？
youtube What is a Scatter Diagram?
散布図 説明 中文版
散布図は中文では”散点图”と呼びます。
散点图简介
散点图是指在回归分析中，数据点在直角坐标系平面上的分布图，散点图表示因变量随自变量而变化的大致趋势，据此可以选择合适的函数对数据点进行拟合。用两组数据构成多个坐标点，考察坐标点的分布，判断两变量之间是否存在某种关联或总结坐标点的分布模式。散点图将序列显示为一组点。值由点在图表中的位置表示。类别由图表中的不同标记表示。散点图通常用于比较跨类别的聚合数据。
参照：百度百科
youtube 散点图
おすすめソフト エクセル統計
搭載機能：基本統計、1標本の推定と検定、2標本の比較、集計表の作成と分析、分散分析・多重比較、ノンパラメトリック検定、生存分析・ハザード分析、時系列分析・曲線のあてはめ、多変量解析、管理図・ROC曲線、特殊なグラフ、ユーティリティなど。
おすすめ ＱＣ七つ道具 参考文献：
| 図解入門ビジネス新QC七つ道具の使い方がよ~くわかる本 | Excelでいつでも使えるQC七つ道具と新QC七つ道具―解析と発想に役立つ14のツール | ポケット図解 QC七つ道具の基本がわかる本 |
【アマゾン おすすめ本 散布図】
コメント