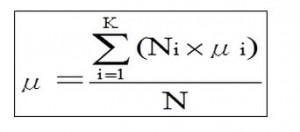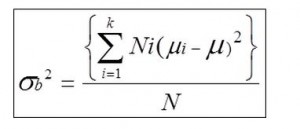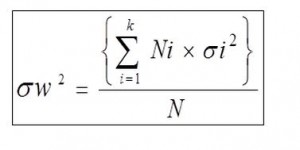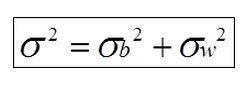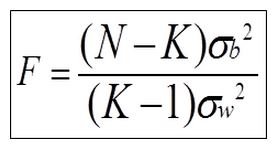stratified sample
A stratified sample is a probability sampling technique in which the researcher divides the entire target population into different subgroups, or strata, and then randomly selects the final subjects proportionally from the different strata. This type of sampling is used when the researcher wants to highlight specific subgroups within the population.
For example, to obtain a stratified sample of university students, the researcher would first organize the population by college class and then select appropriate numbers of freshmen, sophomores, juniors, and seniors. This ensures that the researcher has adequate amounts of subjects from each class in the final sample.
It is important to note that the strata used in stratified sampling must not overlap. Having overlapping subgroups will give some individuals a higher chance of being selected as subjects in the sample. If this happened, it would not be a probability sample.
Some of the most common strata used in stratified random sampling are age, gender, religion, educational attainment, socioeconomic status, and nationality.
When To Use Stratified Sampling
There are many situations in which researchers would choose stratified random sampling over other types of sampling. First, it is used when the researcher wants to highlight a specific subgroup within the population. Stratified sampling is good for this because it ensures the presence of key subgroups within the sample.
Researchers also use stratified random sampling when they want to observe relationships between two or more subgroups. With this type of sampling, the researcher is guaranteed subjects from each subgroup are included in the final sample, whereassimple random sampling does not ensure that subgroups are represented equally or proportionately within the sample.
Researchers who are interested in rare extremes of a population often use stratified random sampling because he or she can representatively sample even the smallest and most inaccessible subgroups of the population. Simple random sampling does not allow this.
Stratified random samples generally require smaller sample sizes, which in turn can save a lot of time, money, and effort for the researchers. This is because this type of sampling technique has a high statistical precision compared to simple random sampling due to the fact that the variability within the subgroups is lower compare to the variations of dealing with an entire population.
Proportionate Stratified Random Sample
in proportional stratified random sampling, the size of each strata is proportionate to the population size of the strata when looked at across the entire population. This means that each stratum has the same sampling fraction.
For example, let’s say you have four strata with population sizes of 200, 400, 600, and 800. If you choose a sampling fraction of ½, this means you must randomly sample 100, 200, 300, and 400 subjects from each stratum respectively. The same sampling fraction is used for each stratum regardless of the differences in population size of the strata.
Disproportionate Stratified Random Sample
In disproportionate stratified random sampling, the different strata do not have the same sampling fractions as each other. For instance, if your four strata contain 200, 400, 600, and 800 people, you may choose to have different sampling fractions for each stratum. Perhaps the first strata with 200 people has a sampling fraction of ½, resulting in 100 people selected for the sample, while the last strata with 800 people has a sampling fraction of ¼, resulting in 200 people selected for the sample.
The precision of using disproportionate stratified random sampling is highly dependent on the sampling fractions chosen and used by the researcher. Here, the researcher must be very careful and know exactly what he or she is doing. Mistakes made in choosing and using sampling fractions could result in a stratum that is overrepresented or underrepresented, resulting in skewed results.
Advantages of Stratified Sampling
Using a stratified sample will always achieve greater precision than a simple random sample, provided that the strata have been chosen so that members of the same stratum are as similar as possible in terms of the characteristic of interest. The greater the differences between the strata, the greater the gain in precision.
Administratively, it is often more convenient to stratify a sample than to select a simple random sample. For instance, interviewers can be trained on how to best deal with a particular age or ethnic group while others are trained on the best way to deal with a different age or ethnic group. This way the interviewers can concentrate on and refine a small set of skills and it is less timely and costly for the researcher.
A final advantage that stratified random sampling has over simple random sampling is that is guarantees better coverage of the population. The researcher has control over the subgroups that are included in the sample, whereas simple random sampling does not guarantee than any one type of person will be included in the final sample.
Disadvantages of Stratified Sampling
One main disadvantage of stratified random sampling is that is can be difficult to identify appropriate strata for a study. A second disadvantage is that it is more complex to organize and analyze the results compared to simple random sampling.
*Quote From “http://sociology.about.com”
Relationship between whole and stratified lot
1)Relationship between the average of the stratified lot and the average of the whole
Formula is as follows:
Number of samples stratified: N1,N2,N3・・・・・Nk
Average of the Stratified lot: μ1,μ2,μ3・・・・μk
Total average=The average of the average of the stratified lot
2)External variance
The variance of the stratified lot called External variance and expressed by σb2
Number of samples stratified: N1,N2,N3・・・・・Nk
Average of the Stratified lot: μ1,μ2,μ3・・・・μk
External variance=The variance of the stratified lot
3)Internal variance
Weighted average of the Total stratified lot called Internal variance andexpressed by σw2
Number of samples stratified: N1,N2,N3・・・・・Nk
variance of stratified Lot: σ1,σ2,σ3・・・・σk
Internal variance=Weighted average of the Total stratified lot
4)Relationship between Total variance and External variance and Internal variance
Variance of all samples is called total variance
Formula of total variance as follows:
Variance Ratio
A measure of the randomness of a return series. Variance ratio is computed by dividing the variance of returns estimated from longer intervals by the variance of returns estimated from shorter intervals, (for the same measurement period), and then normalizing this value to one by dividing it by the ratio of the longer interval to the shorter interval. A variance ratio that is greater than one suggests that the returns series is positively serially correlated or that the shorter interval returns trend within the duration of the longer interval. A variance ratio that is less than one suggests that the return series is negatively serially correlated or that the shorter interval returns tend toward mean reversion within the duration of the longer interval.
N:Whole size
K:The number of split
①When we was collecting something similar and then split
The value of F is greater than the one
Case of F=1237.5
②When we was collecting Random sample and then split
The value of F is a value close to 1
Case of F=1.11375
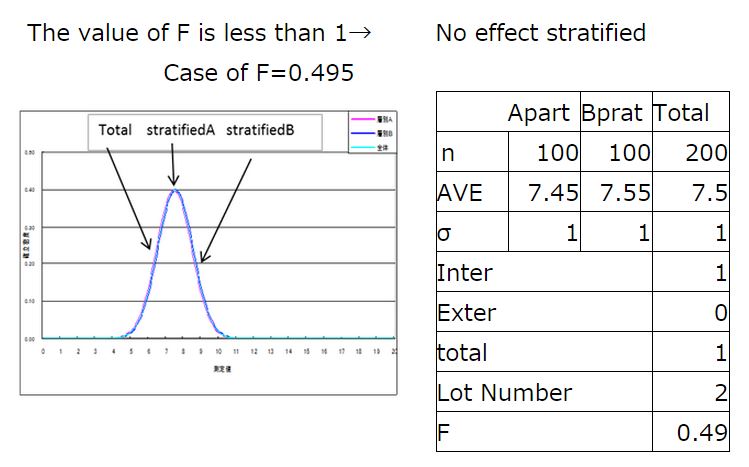
③ No difference in the average value of each lot and then split
The value of F is less than 1→ No effect stratified
Case of F=0.495
Specific cases
①By hour; Hour, day, morning, afternoon, day, night, work started, the end of work, day, week, season
②By Woker: Individuals, age, man, woman, new, old
③By Equipment: Model, the Unit, model, performance, plant, line, mold, jigs separate
④By method: Line speed, working methods, lot, temperature, pressure, speed, rotational force, humidity
⑤By Material: Manufacturer, purchase, stock, purchase time, production lot, ingredient, size
⑥By Measure: Measuring instrument, the measurement, the measurement method
⑦By Test・・・ Inspectors, inspection location, inspection method
⑧Environment: Lighting, temperature, humidity