田口メソッドとは | タグチメソッドとは
タグチメソッドとは日本では品質工学と呼ばれ、田口玄一博士が半世紀をかけて 独力で開発した工学手法です。
タグチメソッドは開発・設計段階で適用されます。 製品が市場に出た時のことを考慮した予測手法という点が従来の品質管理との違いです。
ものを造るのは製造部門の仕事と考えられていますがタグチメソッドは開発・設計段階で バラツキのないものをつくるべきだと主張します。
タグチメソッドは2段階設計法を使用します。はじめにバラツキを減らし、次に目標値に あわせこむという手法です。
タグチメソッド概念 | 田口メソッドによる品質改善ポイント
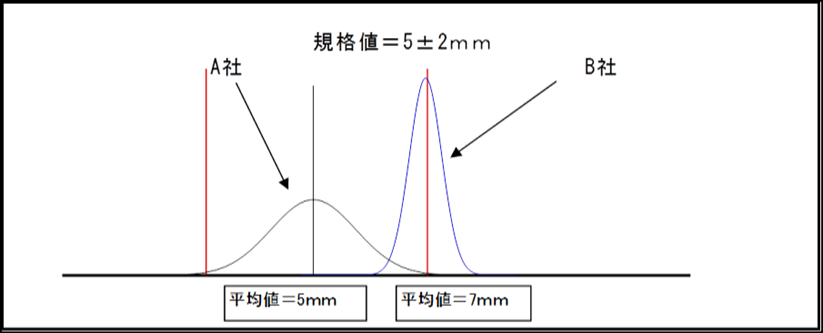
下記グラフに記入しているA社とB社の製品でどちらが技術力のある会社か?
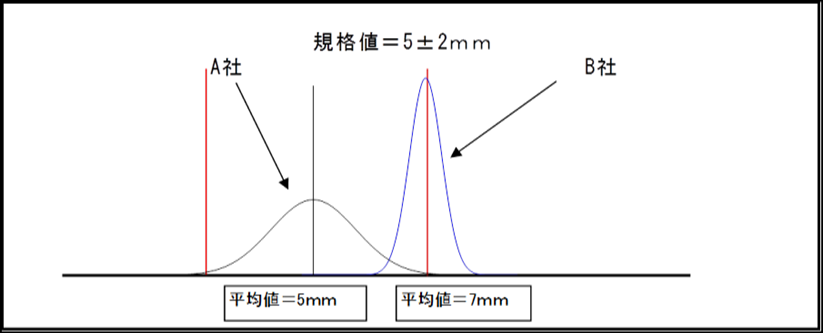
タグチメソッド概念 | 田口メソッドによる品質改善ポイント
従来の品質管理の考え方ではA社のほうが全ての製品が規格値内で技術力が優れていると判断するがタグチメソッドではB社の方が技術力が優れている会社と判断します。
タグチメソッドではバラツキを小さくすることを優先して考えます、平均値を目標値(規格値) に合わせることは容易なのでB社の場合、わずかな時間で容易に平均値が目標値に近づけることが 可能ですがA社がバラツキを小さくすることは容易ではないからです。
弓矢に例えると的から外れてもバラツキがなく当てて人とたまに的にあたるがバラツキが大きい 人の場合的から外れてもバラツキがなく当てて人のほうが少しのコツで短時間で弓矢が上達する のに比較してたまに的にあたるがバラツキが大きい人はなかなか上達しません。
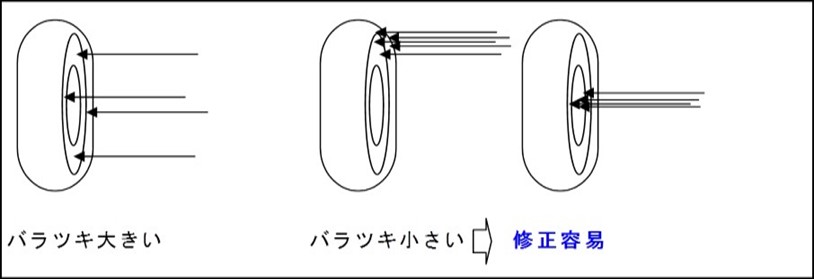
バラツキσの考え方 | バラツキとは?
砂時計の開発 | エクセルによる田口メソッド事例
1)バラツキの表し方
タグチメソッドではバラツキの尺度をSN比で表します。 砂時計の場合はSN比の定義式は次式となります。
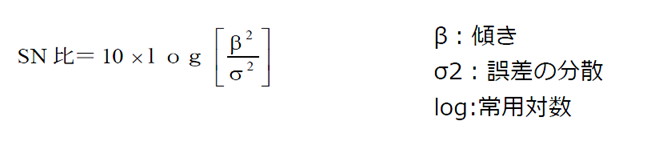
*上記式でバラツキを示す分散が分母にあることから、バラツキが小さいと SN比が大きくなります。
2)砂時計の設計
砂の量Mを信号因子と呼び、Mを5g、10g、15gと変化させた時、砂時計の時間yを 5分、10分、15分にすることを考えます。
砂の量の変化にともない砂時計の時間が動的に変化することから、これを動特性といいます。 Mを信号因子としyを特性値とするMとyの関係式は原点を通る一次比例式で表せます。
y =β×M
信号因子Mと時間yの理想的な関係
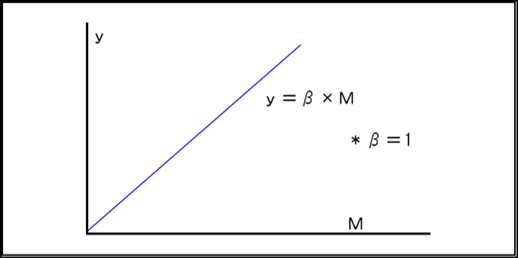
信号因子Mと時間yの理想的な関係
信号因子Mと時間yの理想的な関係は上記グラフのようになりますが 実際上は使用条件によって誤差が入ってくる為に下記の表およびグラフ のようになります。
これら誤差(温度変化、湿度、振動etc)を誤差因子と呼びます。 タグチメソッドではわざと悪条件でも実験し悪条件でも正確な時を刻む 砂時計を開発します。
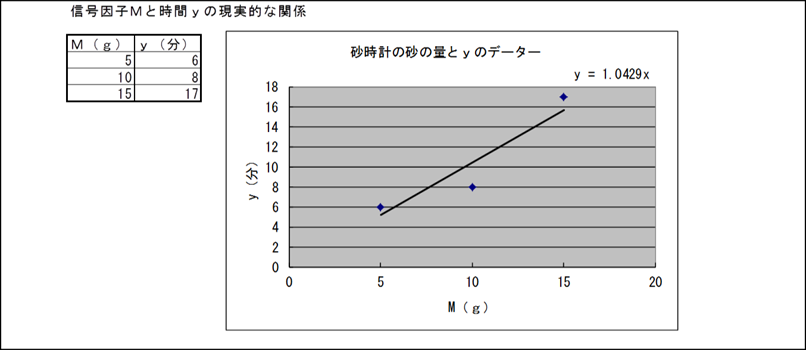
信号因子Mと時間yの現実的な関係
制御因子と割付 | 直行表
制御因子を直交表に割り付けることにより、代表的な組み合わせの実験だけで、全体を網羅した 実験が実現できます。
砂時計事例・・制御因子と水準
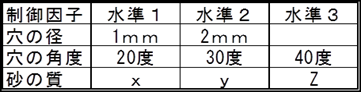
砂時計事例・・制御因子と水準
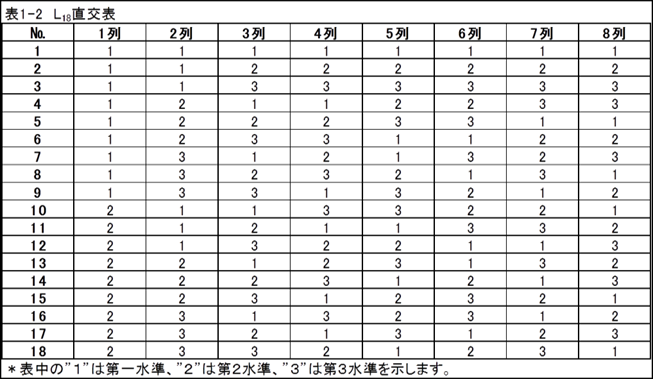
砂時計事例・・直交表
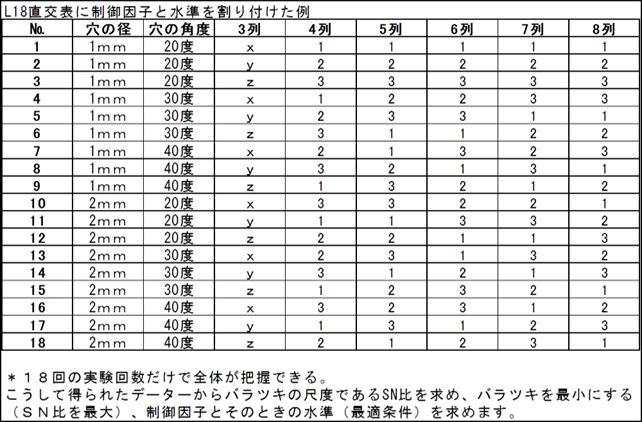
砂時計事例・・直交表2
データー解析はエクセル回帰分析を使用 | sn比
変動分解法を用いてSN比を求めると精度が高いデーターが得られるが計算が難解なので エクセルの回帰分析を用いた簡便法を用いても実用的に問題のないSN比が求まるのでここでは エクセルの回帰分析を用いる。
静特性と動特性 | エクセルによる田口メソッド解析
a)静特性
いかなる条件でも出力が一定となる特性のことで砂時計の例ではどのような使用環境下でも 正確に「5分」の時を刻む砂時計を開発する場合のことをいいます。 静特性はその特性の性質から次のように細分されます。
①望目特性
乾電池のようにある一定の目標値がある特性(非負)
②ゼロ望目特性
位置ずれのように目標値がゼロである特性
③望小特性
騒音のように特性値が小さければ小さいほどよい特性(非負)
④望大特性
接着強度のように特性値が大きければ大きいほど良い特性(非負)
動特性
特性とは車のアクセルとスピードの関係のように入力の変化に対応して出力が変化する特性 のことで砂時計の例では「5分」だけ「10分」だけの砂時計をそれぞれの静特性で開発する のではなく「5分」でも「10分」でもどのような時間でも対応できる砂時計を開発する場合 のことを言動います
1.相関とは
相関とはある量(x)とある量(y)との関係を表すもので、散布図を描けばよくわかります。 その関係が指標となる相関係数rは-1~1の値で±に近いほど関係する度合いが強く 0に近いほどその関係度合いがないことを意味します。 rを求める前にはまず下式から「相関」があるのかないのかを把握してから求めます。
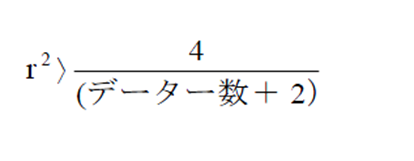
相関性の確認
散布図で関係(相関)を見る
散布図を描くとき原因系となるデーターを左側に結果となるデーターを右側に来るような表にしておくと 散布図では原因が横軸に結果系が縦軸に描けます
下記がコーヒー粉量とコーヒー濃度の関係の相関と回帰の事例です。
表2-1 コーヒー粉量とコーヒー濃度のデータ
(Excelでは右側のデータが縦軸(y軸)になります)
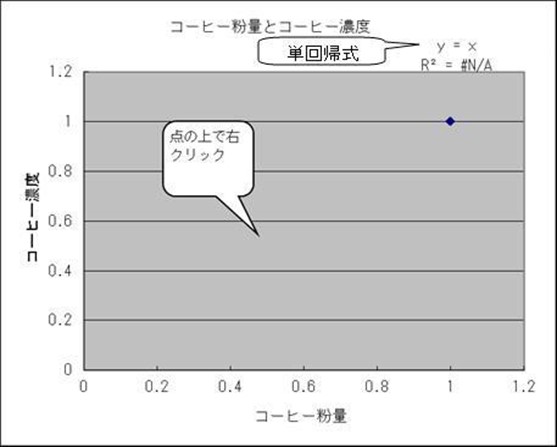
田口メソッド 散布図
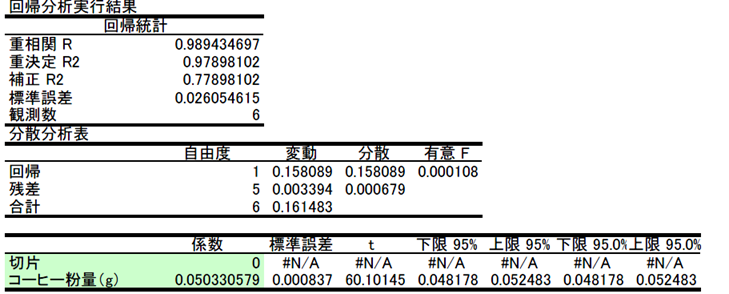
田口メソッド 回帰分析事例
■「分析ツール」による相関係数の求め方
①「ツール」→「分析ツール」→「相関」
②「入力範囲」に「コーヒー粉量」欄のラベルから「コーヒー濃度」欄最後のデーター「0.90」まで選択し「先頭行をラベルとして使用」の左の欄にチェツクを入れて「OK」ボタンをクリックすると下記の表が 表示される。
コーヒー粉量とコーヒーも濃度の相関実行結果

田口メソッド解析事例
結果:上記判定式が成立するために相関があると判定!
3.散布図グラフ作成方法
1)該当データーセルを選択(下図、緑部分)し、「グラフウィザード」ボタンを押す
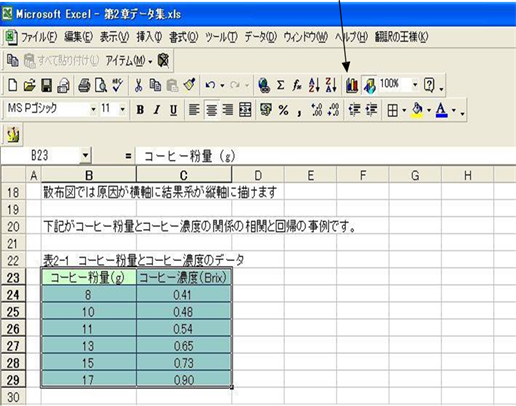
散布図グラフ作成方法
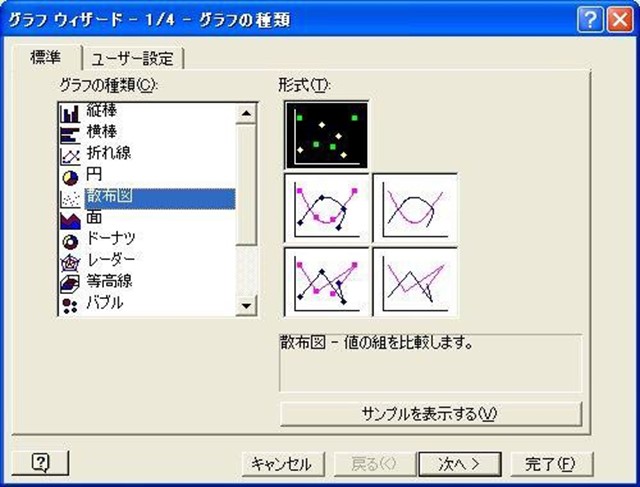
散布図グラフ作成方法2
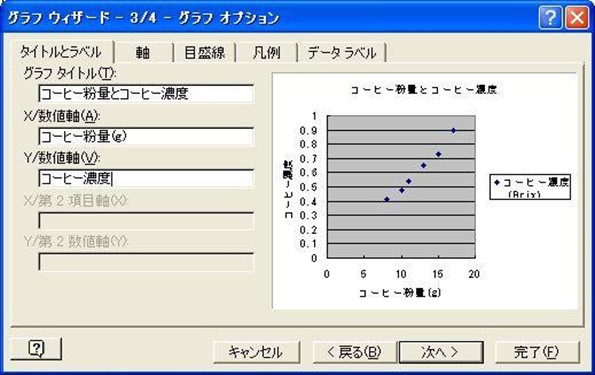
散布図グラフ作成方法3
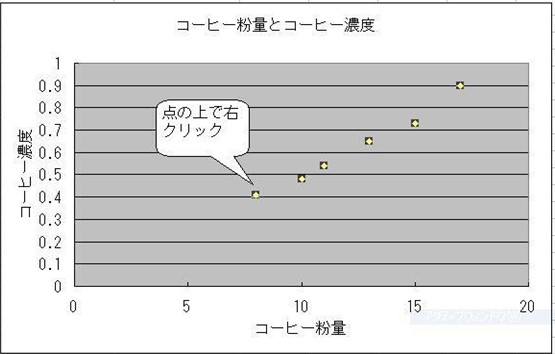
散布図グラフ作成方法4
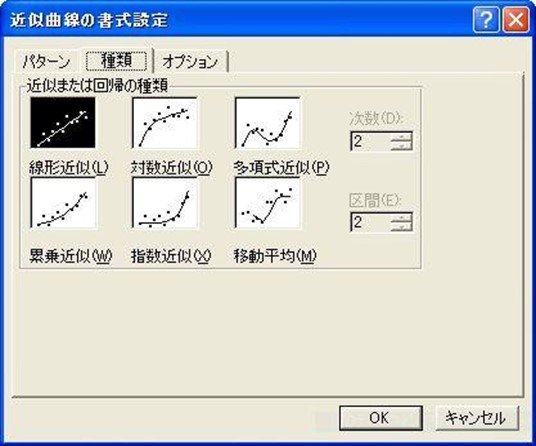
散布図グラフ作成方法5
2)次に散布図を選択
3)次へのボタンを押し、下記のようにグラフタイトル、x、Y数値軸にタイトル記入
4)完了ボタンを押してグラフを完了させる。 グラフ上のデーター点をクリックし近似曲線の書式説定を表示させる。
5)線形近似を選び次へのボタンを押す。
6)オプションタブで切片(s)=0及びグラフに数式表示するを選ぶ
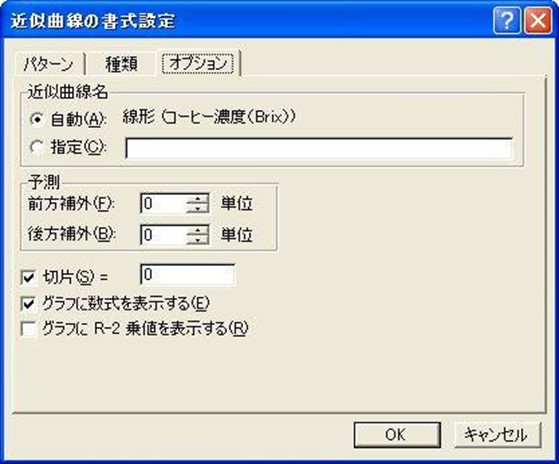
散布図グラフ作成方法6
4.分析ツールによる回帰分析(単回帰式)
1)「ツール」→「分析ツール」→「回帰分析」を選択
回帰分析 ダイヤログボックスが表示されるので入力Y範囲に結果系のデーター、入力X範囲に原因系 データーを入力。次に「ラベル」と「定数に0を使用」の左欄にチェツクをいれて「OK」ボタンを押す
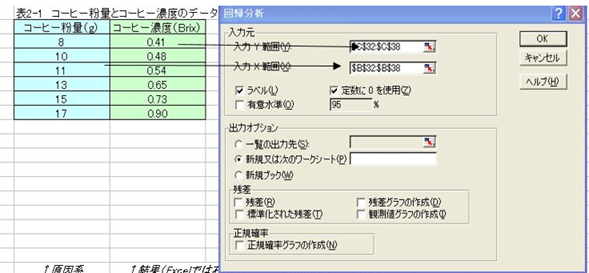
分析ツールによる回帰分析
2)次に出力先を指定して「OK」を押すと回帰分析の実行結果が表示される。
■分析ツール(アドイン)のインストール方法
「ツール」→「アドイン」→「分析ツール」及び「分析ツール-VBA関数」をチェツク→「OK」ボタンを押す
*インストールの際にはマイクロソフトOffice用CD-ROMが必要になるの用意しておく。
重回帰分析とは?
重回帰分析とはいくつかの説明変数でひとつの被説明変数を説明する式のことでまとめて説明することに精度が良くなります。 事例:
賃貸マンションの物件データを使用してバス時間、専用面積、築後、賃料にどのような 関係があるかを調べます。
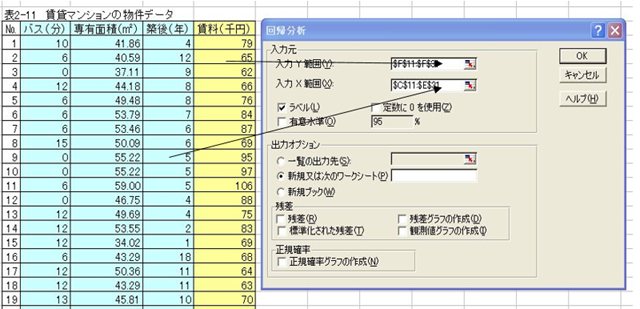
表2-11 賃貸マンションの物件データ
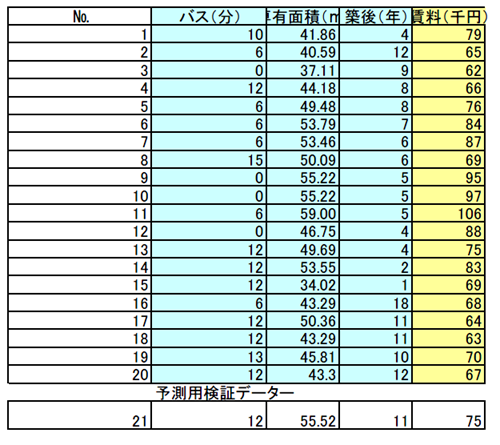
重回帰分析事例データー
1)はじめに項目どうしの関係を相関係数rから割り出します
次に入力範囲に「バス(分)」欄のラベルから「賃料(千円)」欄のデーター「67」までをドラックして選択して「先頭行をラベルとして使用」の左の欄にチェツクを入れて「OK」ボタンをクリ「ツール」→「分析ツール」→「相関」→「OK」ボタンを押す。
クリックすると下記の相関関係r表が作成されます。
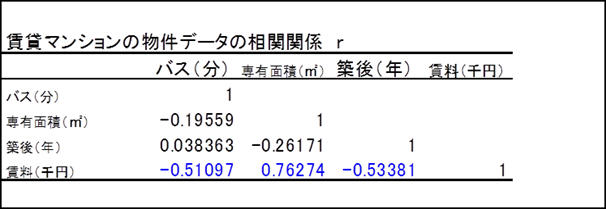
相関関係r表
2)相関判定:
次に下記の式にrを代入して相関判定をします。

相関判定
データーが20ですからr2が4÷(20+2)=0.182より大きい相関係数に相関があると判定されます。
結果:
賃貸マンションの物件データの相関関係 r表にて青色で表示したものが相関があると判定されたものです。
2.賃料の重回帰分析
重回帰式は一般にxi (i=1・・・・,k)を説明変数、yを被説明変数として

と表します。回帰係数は誤差の自乗和を最小にする最小自乗法を用います
賃貸マンションの物件データーからExcelの回帰分析で重回帰式を求める。
①「ツール」→「分析ツール」→「回帰分析」→「OK」
②「入力Y範囲」には「賃料(千(円)」欄ラベルからデーター「67」までの範囲を設定する。
③「入力X範囲」には「バス(分)」欄ラベルからデーター「筑後(年)」欄のデーター「12」までの全範囲
を設定する。
④「ラベル」の左の欄にチェツクを入れて「OK」ボタンをクリックします。
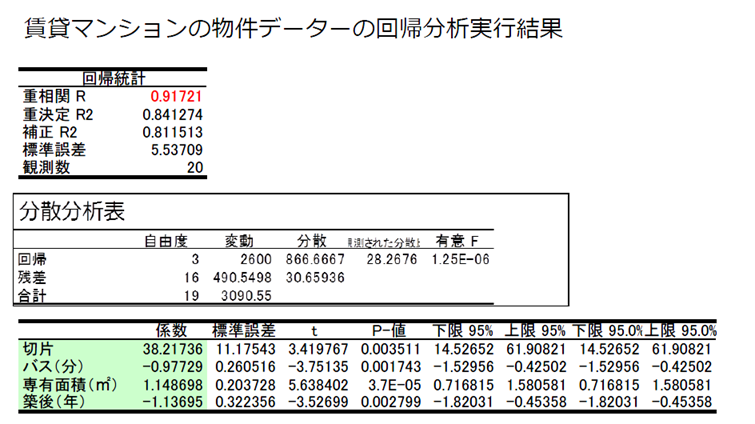
賃貸マンションの物件データの回帰分析
物件データの回帰分析
物件データの回帰分析2
3.重回帰分析の目的
重回帰分析の目的は「予測」と「要因分析」です。
「予測」は重回帰式から求まります。
「要因分析」は影響度で見ます。
a)賃料の予測
賃料=38.22-0.98×バス(分)+1.15×専用面積(m2)-1.14×築後(年)
=38.22-0.98×13+1.15×60-1.14×6=87.6(千円)
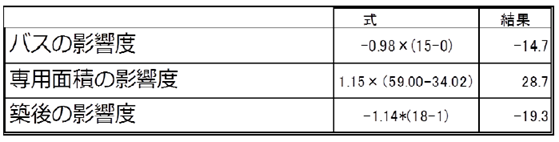
b)要因分析
影響度=回帰係数×レンジ(範囲)
*レンジ:説明変数のデーターの最大値内-最小値
定性的なデーターの解析
少ない、多いとかの定性的なデーターでも解析はできます。
定性的なデーターを水準ごとに0,1データーに置き換えることでExcelの回帰分析が実行できる。
1)定性的データーの解析事例
①下記のおいしくご飯を炊く為の条件を0,1の水準に置き換えて表2 おいしいご飯を炊く条件を回帰分析に作り直したデーターに置き換えます。
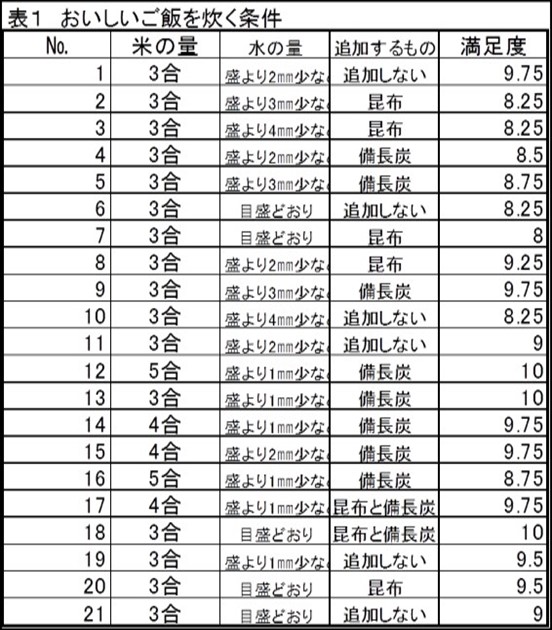
定性的データーの解析事例
②水準1、2に変換した表
表2 おいしいご飯を炊く条件を回帰分析用に作り直したデータ
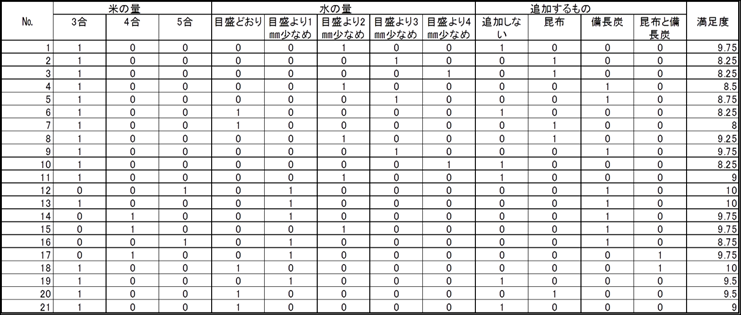
回帰分析用に作り直したデータ
③冗長データーの削除 Excelでは削ってもわかる情報を含めて実行すると、情報が冗長であると判断してエラーが生じる為に冗長データーを削除する。
表3 回帰分析実行用に1要因につき1水準ずつ削除したデータ
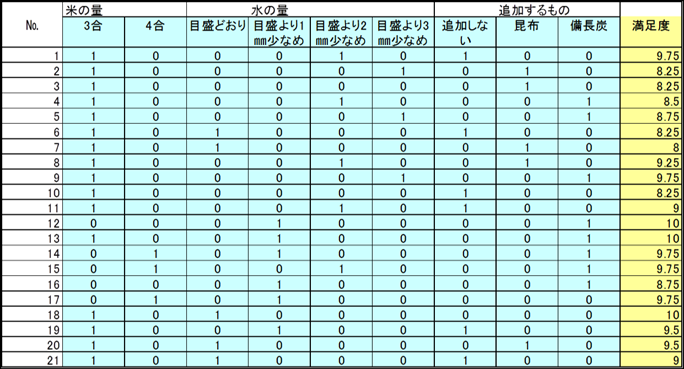
回帰分析実行用に1要因につき1水準ずつ削除したデータ
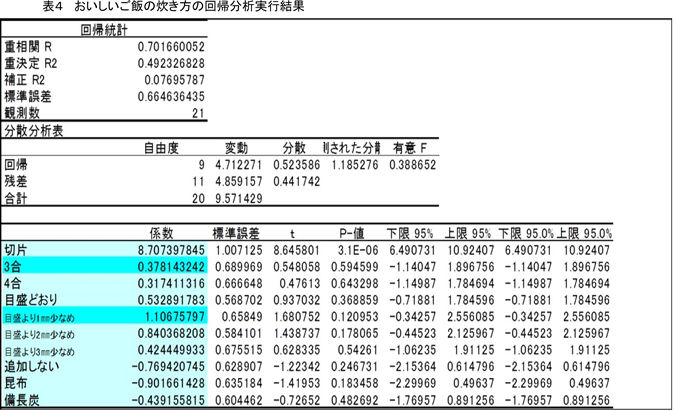
おいしいご飯を炊く条件を回帰分析結果
満足度が一番高い、ご飯の炊き方(最適条件)は米の量が3合、水の量が目盛より1mm少なめ 追加するものが『昆布と備長炭』の組み合わせ
y=8.71+0.38+1.11(目盛より1mm少なめ)+0(昆布と備長炭)=10.20
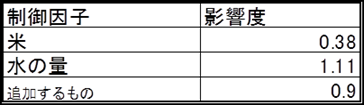
定性的なデーターは各要因の回帰係数のレンジ(範囲)から影響度を求めます 米の影響度:0.38-0=0.38
水の量の影響度:1.11-0=1.11
追加するものの影響度:0-(-0.90)=0.90
SN比とは?
SN比とは機能の安定性を表す尺度のことで通信工学で使われる信号対ノイズ比と同じ意味のものです。 SN比はした図に示すように信号とノイズのパワーの比でこの対数を10倍したものをいい、db(デシベル) という単位で表します
SN比の種類
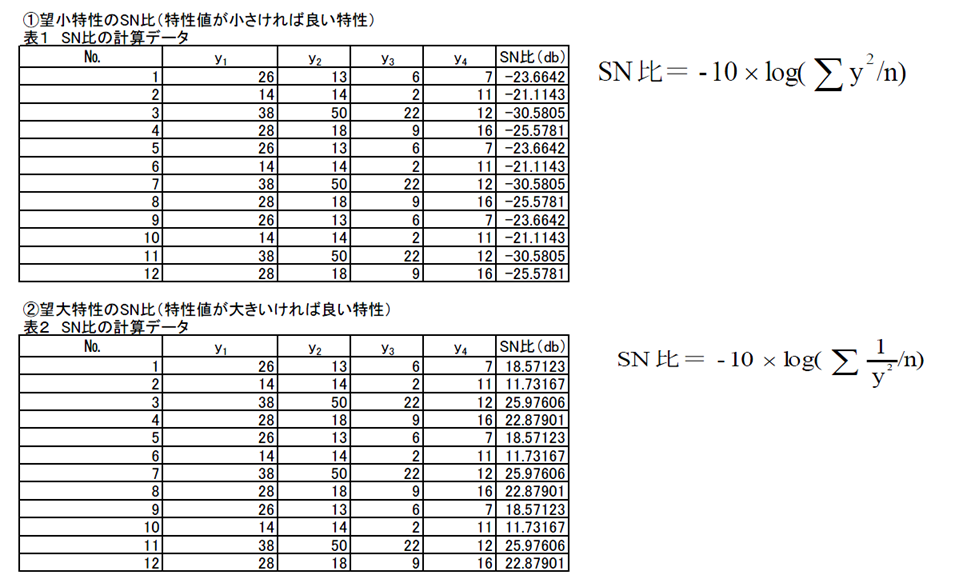
SN比の種類
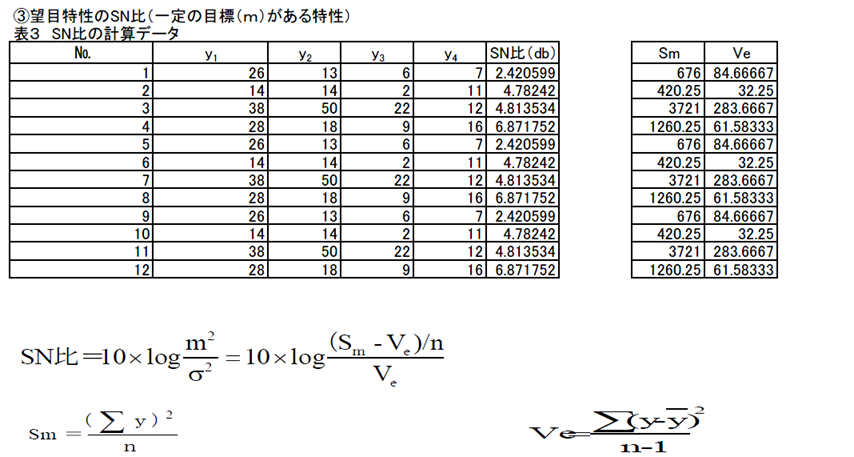
SN比の計算データー
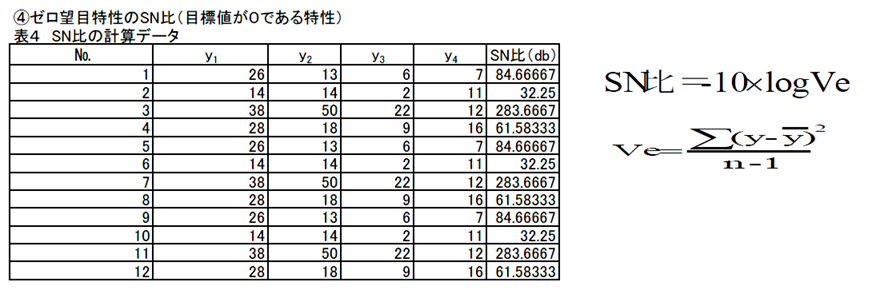
SN比の計算データー2



















コメント