バスタブ曲線

バスタブ曲線（故障率曲線）　　【イラスト図解】

バスタブ曲線（故障率曲線）　　【イラスト図解】

英語：bath-tub curve　　　　　　　　　　　　　　　中国語：浴缸曲线

バスタブ曲線（故障率曲線）とは

　修理を施さない場合の装置，機器にみられる典型的な故障率関数の曲線。
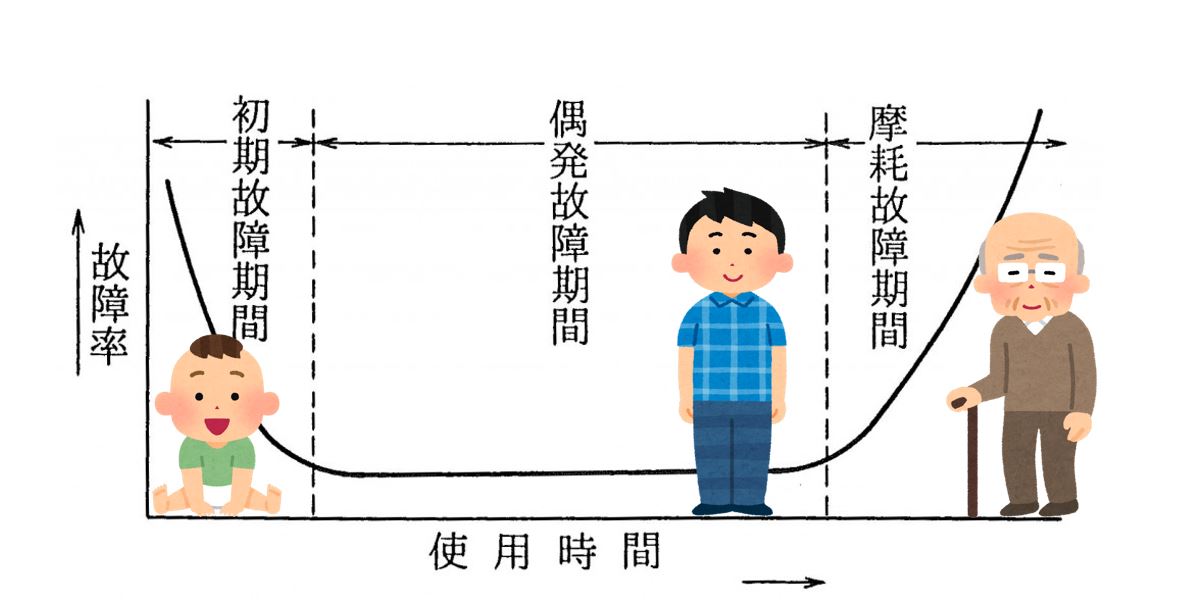
浴槽の形に似ていることからこの名前がついている。下図の曲線の中で，期間Ｉは，人間の場合の幼児期に対応して故障率が急激に低下する初期故障期間という．期間IIは，長期にわたり故障率が一定の期間で偶発故障期間といい，人間の場合の青年期に対応している。

ここでは故障率が規定の値より低く，しかもなるべく小さく，またその持続時間，つまり図の耐用寿命がなるべく長いことが望ましい．期間Ⅲは，経時劣化などによる故障率が上昇する摩耗故障期間といい,人間の場合の老年期に当たり，予防保全(PM)とか事後保全(ＣＭ)などの手を打って上昇する故障率を切り下げる必要がある。
　修理系の場合には，PMやＣＭを施すと，保全や取替の時期によって構成部品
の寿命がランダムになり，定常状態では故障率は一定になると考えられる。

バスタブ曲線

引用先：クォリティーマネジメント用語辞典　日本規格協会

わかりやすく　バスタブ曲線（故障率曲線）

故障は初期故障、偶然故障、磨耗故障の３時期に分けられ縦軸に故障率、横軸に時間を設定してグラフで表すと下記のグラフのようになる。この曲線はバスタブ曲線（bathtub curve)と呼ばれている故障率曲線である

【初期故障】 early failure 新製品を初めて市場に出しお客さんが使用開始するとすぐに発生する故障を初期不良という。

原因としては設計、製造上の欠点、使用環境との不適合である。

初期不良を低減する方法としてはデバギングがある（debugging :虫を追い出す意味）これは製品を使用開始前又は使用開始後の初期に動作させて欠点を除去する方法である。また、スクリーング（選別：screening)も初期不良を低減するための有効な方法です。

スクリーニングは製品をつくっている工程及び完成品について目視、漏れ、高温保存などの非破壊試験を全数に対して行い欠陥のある品物を取り除きます。

【偶発故障】 random failure

初期故障期間を過ぎ磨耗故障期間に至る以前の時期に偶発的に起こる故障人間でいえば青年期に当たり、製品の故障が少ないのが特徴です。

この期間の長さを「耐用寿命」と言います

【磨耗故障】 wear out failure

品物を長い間使用すると疲労、磨耗、老化などによって品物のいたみが激しく一斉に故障が続発する状態になります

この期間を「磨耗故障」と呼びます。

予防策としては予防保全：ＰＭがあります、ＰＭによって磨耗故障に入る前に不具合と思われる部品を交換すればよいのです

関連記事：信頼性　| 信頼性工学 | 信頼性試験

バスタブ曲線具体例

実際にそれぞれの故障期にはどのような傾向があるのか、パソコン及び自動車の故障事例を紹介。

パソコンの故障事例

パソコンの故障事例には、以下のような傾向があります。

初期故障期	新しいコンピューターが起動しない、ディスプレイに映像が表示されないなどの不具合が報告されています
偶発故障期	一般的な使用状況で正常に機能し続けることが期待されるフェーズです
磨耗故障期	経年劣化によりバッテリーの持ちが悪化したり、ハードウェアの故障が頻発したりする可能性が高まっていきます

自動車の故障事例

自動車の故障事例には、以下のような傾向があります。

初期故障期	新車がエンジン不調や不安定な運転感を示すなどの不具合が報告されています
偶発故障期	一般的な使用状況で正常に機能し続けることが期待されるフェーズです
磨耗故障期	走行距離や年数の経過により、エンジンやサスペンションなどの部品の劣化や故障が増え、老朽化が進行します。車両の性能や安全性に問題が生じる場合もあります。