プロジェクト管理
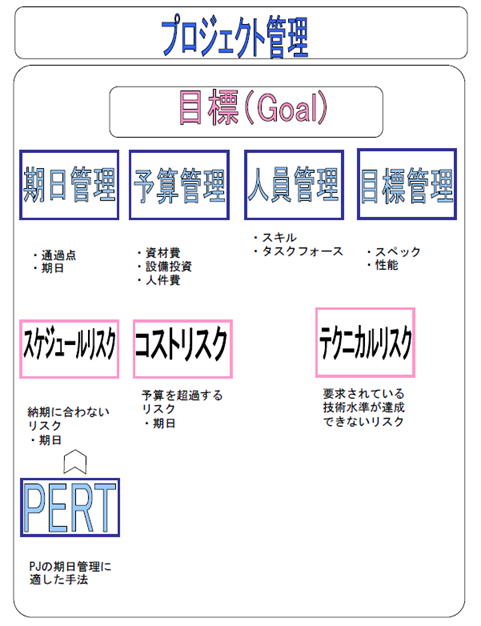
プロジェクトとは、明確な目標(ゴール)が定められた活動である。そして、その活動には 、時間、予算、人員など限られた資源が割り当てられている。その有限の資源を管理するために図にあるように期日管理、予算管理人員管理、目標管理が行われる。
期日管理
期日管理では、予定した期日までにプロジェクトが終了するための管理が行われる。 最終期日を守るために、通過点となる期日の管理も行われる。後に説明する「PERT」などの期日 管理手法を使っての管理が行われる。期日を過ぎてしまっても完了しないプロジェクトでは、 次に説明する予算がオーバーとともにプロジェクト自体の価値が減少するリスクがある。
予算管理
資金オーバーを起こした場合に追加的な資金を得られるのならよいが、そうでない場合には 資金ショートした時点でプロジェクト全体が中断ということもありうる。プロジェクトで管理 すべき予算は、資材費、設備投資、人件費など多岐にわたっており、それぞれについて確実な 管理を行う必要がある。
人員管理
プロジェクトによっては単純労働だけではなく、高度なスキルを持った人材が必要な場合も ある。それぞれの必要なスキルを持った人を確保し、また、それらの人たちを必要に応じてタスクフォースなどでチーム作りを行うことも人員管理で必要となる。
目標管理
プロジエクトに対して求められている成果物のスペックや性能が要求に合致しているか否か の管理を行う。要求されている結果を出すことがプロジエクトの目標である。
期日、予算、人員、目標のそれぞれの管理を正確に行うことによって、プロジエクトを完遂 できる。
プロジェクト管理とは
PERTによる期日管理
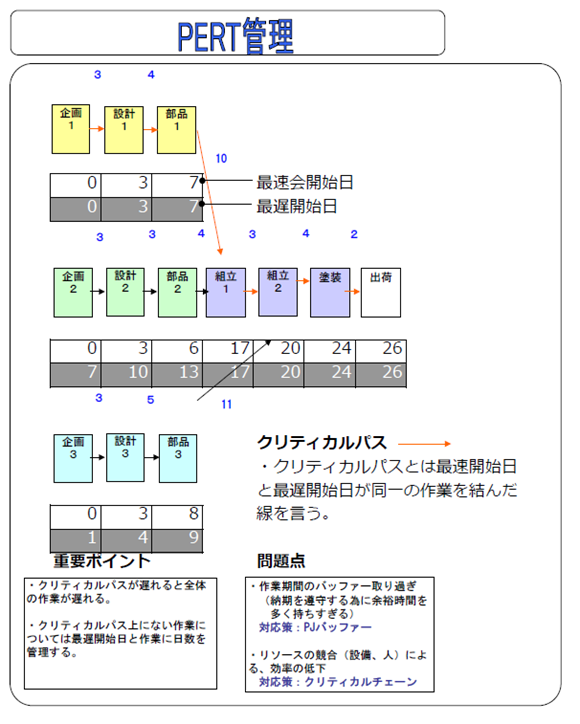
PERT(Program Evaluation and Review Technique)は、プロジエクトの期日管理に適した 管理手法である。PERTでは、図にあるように、すべての作業の流れを、その作葉開始日と 作業日数を勘案しながら作成していく。
たとえば、この図では、企画からプロジェクドがスタートする。企画1,2,3それぞれの 最速開始日はO日目であり、その作業日数は3日間である。画が終了した時点で設計が開始 できるが、部品1、部品2、部品3のそれぞれの設計を並行して行うことができる(設計1,2,3) それぞれの設計が終わった時点で、部品1,2,3の製造が始まるが、部品、1、2の両方が完成 した時点でそれを組立1の作業で組み立てる。さらに組立1で完成した部品に、部品3を組み 立てる(組立2)。
組立2が終了するとそれにペイントを施し、さらに出荷ということになる。それぞれの作業 に必要な日数はその作業の後ろの矢印の上に示している。
さらに、それぞれの作業には最速開始日と最遅開始日が示されている。箱の上段が最速開始日、 下段が最遅開始日だ。たとえば設計1の最速開始日と最遅開始日はどちらも3日目だ。
最速開始日と最遅開始日が違っているものもある。部品1の設計と製造に合計で14日 (設計4日、製造10日)が必要なため、部品2の設計開始は最も遅い場合には10日目でも 間に合い、部品製造開始は13日まで待っても良いと いう事になる。
また、同様に部品3の設計開始は最遅で4日目、製造開始は9日目である。その後の組立2、 ペイント、出荷は、最速開始日、も最遅開始日も同じである。
このようにPERTでは、それぞれの作業の手順を決定し、それに要する時間を予測した上で、 その作業期間から、それぞれの作業の最速開始日と最遅開始日を決めていくものである。
それにより、次項で説明する「クリティカルパス」を特定し、プロジェクトの期日管理の精度 を高めることが可能となる。
PERT管理
PERTによる期日管理
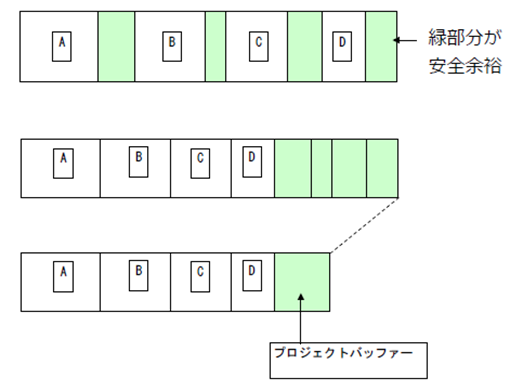
プロジェクトの各作業が安全余裕を持っている場合にその合計が膨大になり、しかも 大半はムダになっている可能性が高い。個々の作業の安全余裕を集約してそれを 「プロジェクトバッファー」として持つことにより安全余裕の大きなムダを削減する ことができる。
プロジェクトバッファー
■学生症候群
ギリギリまで仕事を始めない習性
■パーキンソンの法則
与えられた時間すべてを使おうとする習性
クリティカルチェーン
PERTの問題点のひとつとして、人材や設備などのリソースが競合することがあるがTOCでは、その解消策を捉示している。
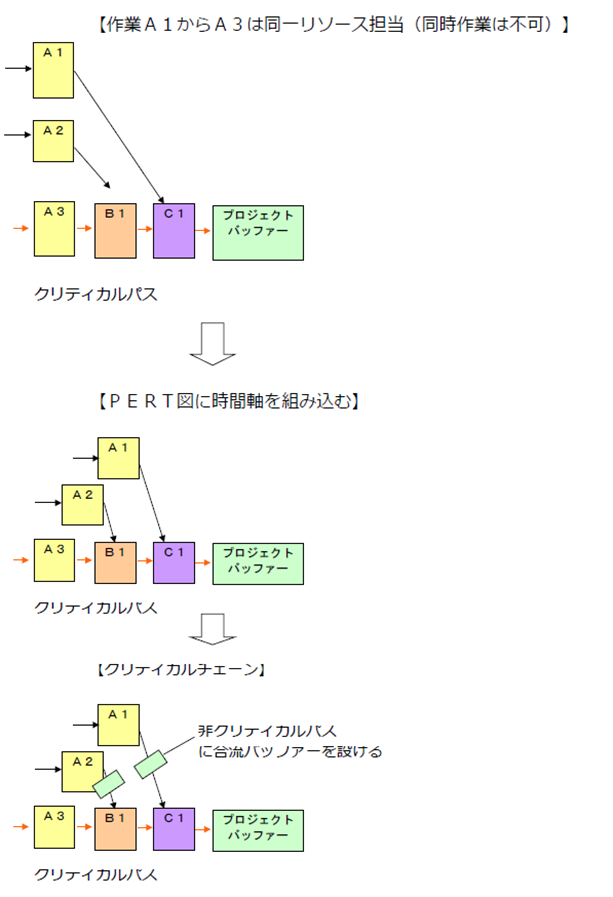
ひとつは、同時並行で進むことができると想定していた作業のうち、リソースが競合するも のについては、「時問軸」の概念をとり入れることにより解決しようとするものである。図の例 では、A1,A2,A3、の作業でリソースが競合する場合に、クリティカルパス上のA3作業終了後にA2、 さらにA2終了後にA1の作業を行うように時間軸を考慮した作業スケジュールを想定する。
さらに、所定の作業が最初に想定した時間通りに進めばよいが、その作業が遅延した場合に はその作業がクリティカルパス上にないにしても、合流が遅れることによりクリティカルパスの作業に遅延が生じる可能性がある。そのリスクを回避するために、それぞれの作業に、合流 に遅れないようにする「合流バッファー」を設ける。
クリティカルパス上の作業は、プロジェクト全体での安全余裕を管理するプロジェクトバッファーで調整するが、クリティカルパス上以外の作業では、余裕時間を持たせることが可能なため、その 余裕時間をあらかじめ合流バッファーとして持つことにより、合流の遅延がクリティカルパスを遅ら せることのないようにする。具体的には、最遅開始日を合流バッファー分だけ早め、最後に合流 バッファを設ける。
このように、TOCでは、PERTに時問軸の概念と合流バッファーをとり入れることにより、より 精度の高いプロジエクト管理が可能となる。このように改善されたクリティカルパスのことを TOCはクリティカルチェーンと呼ぶ
クリティカルチェーン
思考プロセス
■論理的思考
TOCでは、ポトルネックを最大活用する生産プロセス、スループット会計など、生産性を 最犬限に高め、スループットを極大化することに焦点があてられがちだ。しかし、TOCが適 用できるのはそれだけではない。
TOCでは、生産性の向上だけでなく、ビジネスや家庭生活において発生するさまざまな問題 を解決する手法である「思考プロセス」という問題解決手法がある。この方法を学ぶことは、 問題点の発見や解決において、論理的思考や客観的意思決定の方法を体得する上で、非常に有 用なことだ。
日本では、これまで往々にして直感やそれほど合理的でない意思決定方法を使ってきたが 論理的な問題発見や解決方法を取得することで、より精度の高い問題解決、意思決定を行うことができるだろう。
■思考プロセスの登場の背景
TOCでは、物埋的制約を解消するために、ボトルネックを発見し、それをドラム・バッファ ー・ロープなどにより最大活用し、生産性を最大限に高めることを行うが、それを行えば、どこかで、供給量が需要を上回る事態に直面することにもなりうる。
また、企業内部の戦略や戦術のまずさから、せっかく高めた生産能力を十分に活用できないこともある(これらを「市場制約」や「方針制約」ということは先に説明した。
市場制約解消のためのマーケティング戦略の策定や、方針制約である企来内部の管理会計な ど評価方法などの問題点を解消するために、問題点の発見、その解消法を見出す手法が必要と なった、いいかえれば問題点発見時に「何を変える」かを見定め、それを「何に変える」 か、そして「どのように変える」かを発見する手法がTOCでいう「思考プロセス」である。
■課題の共有
思考プロセス活用により、水面下の課題を浮き彫りにし、その解決策を見出していくのだが、その過程において、思考プロセスに参加したメンバー全員で課題の共有ができるようになる。
単に問題発見、解決手段を発見するというだけでなく、何が問題でどう変えるかということに ついて課題の共有ができることが問題点解決において重要であることはいうまでもない。
問題を解決するにあたり、何が問題点であるかを発見し、それをどのような状態に変えるの が望ましいか、また、どうやって変えるのがよいのかを考えなければならない。言いかえれば、 「何を」、「何に」、「どのように」、変えるかを考えるのである。
また、問題点発見にあたっても、何が本質的な問題(TOCでは「中核問題」という)で、何がそれによって派生的に発生した問題(「UDE(Undesirable Effect:好ましくない結果) なのかを区別しなければならない。 思考プロセスにおいては、以下の体系で問題点を解決していく。
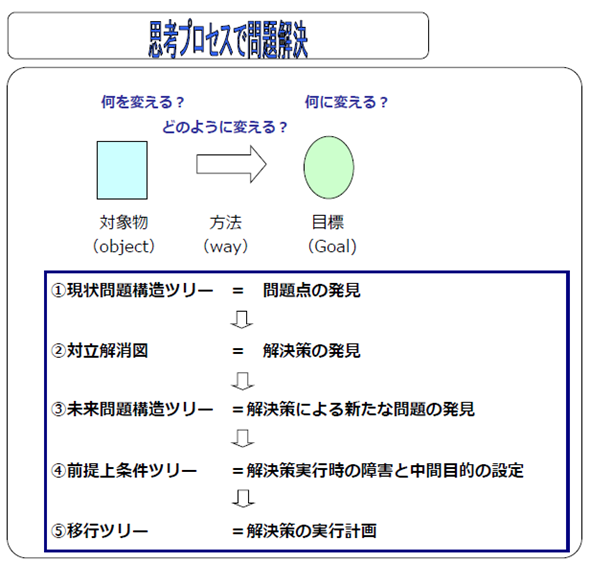
①現状問題構造ツリー:問題点発見のための手法。
UDEを列挙し、どのUDEがどのUDEの原因であるのかを構造化していく。構造化した結果 が木のようになるので「ツリー」と呼んでいる。構造化することにより、中核問題が発見しやすくなる。
中核問題とは、それが解決されれば大多数のUDEが解消する問題をいう。発見の過程で、 真の問題は何かをメンバーが認識し、組織の問題点を体系的に杷握することができる。
- 対立解消図:発見された中核問題を解決するための改善方法を考え出すための手法。
解決策には、相容れない対立点が存在することがあるが、この対立解消ツリーを用いること により、対立点を発展的に解消する「ブレークスルー」案を見出しやすくする。
③未来問題構造ツリー:現状問題構造ツリーの中核問題を、対立解消ツリーで見出したブレークスルー案などを用いることにより発見した改善策をもとに、現状問題解消ツリー を作りなおしたもの。それにより、新たな問題が発生しないかどうかを検証する。
- 前提条件ツリー:解決案を実行していく際に発生する障害ととそれを解決するための中間 目的の流れを示すツリー。
⑤移行ツリー:前提条件ツリーを踏まえて目的達成達成のためのプロセスを示すツリー。
思考プロセス
問題構造ツリー
企業活動を続けていくと、「売上げが伸びない」、「残業が多い」などさまざまな問題が発生する。
経営者はそれぞれの問題に対して優先順位をつけ解決していこうとするが、うまく解決できない場合も少なくない。それは、対応の対象とする問題が、実はそれよりも、もっと根本的に存在 する問題によって引き起こされた結果であって、その根本的な問題を発見し解消しない限り、問題点は解決されない。
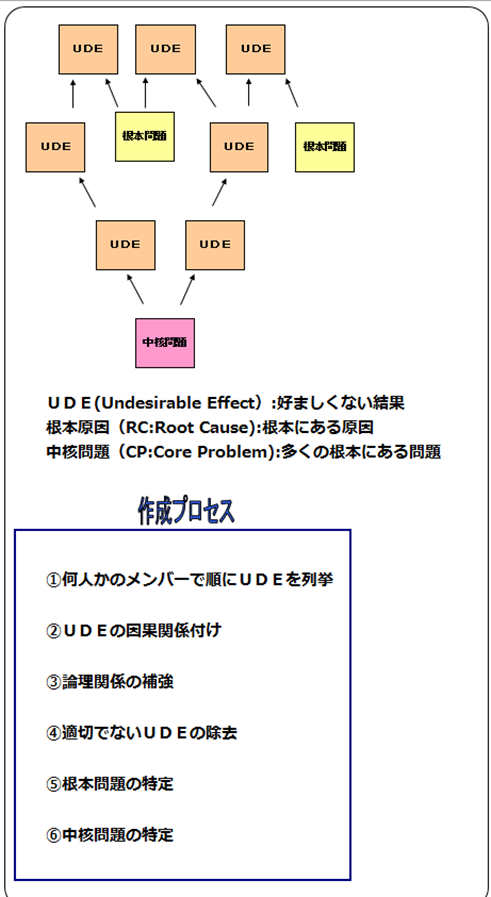
言いかえれば、表面的な現象を追うばかりでその解決を「モグラたたき」のように行っても、 次から次にまた、「モグラ」が発生する。TOCでは、結果的に引き起こされる問題の根本にあ る問題を、「根本原因(Root Case:RC)と呼び、その結果、引き起こされる問題点を 好ましくない結果(Undeirable Effect)として考える。
また多くにUDEの原因となるRCのことを「中核問題」(Core Problem:CP)と位置づけている。 このCPの解消こそが本当の問題解決ということになる。
具体的に現状問題構造ツリーを作るには次のような方法をとる。
-
何人かのメンバーで、UDEを順に列挙してゆく。「仕事量が多い」、「社員教育制度が貧 弱」、「多くの職員の能力不足」、「十分なアウトプットを出せない」、「特定の人に仕事が 集中する」など、思いつくことをどんどん列挙していく。10から20くらい出たところでいったんUDEの列挙をやめる。このときに、問題点を付箋紙などに書いていくと後で並び替えを行う ときに便利だ。
②①で列挙した問題を因果関係付けする。具体的には「○○だから△△となる」というふ うに、原因となるものが下にきてその結果が上にくるようにする。「△△となるのは○○ が原因である」と考えてもよい。 ①の例では、『特定の人に仕事が集中する』となるのは『多くの職員の能力不足』が原 因」であり、さらに、『多くの職員の能力不足』となるのは『社員教育制度が貧弱」が 原因となるから、図のように三つの因果関係が上下に並ぶツリーとなる。さらに、「特 定の人に仕事が集中する」かつ「仕事量が多い」ので「十分なアウトプットが出ない」 という結果となる。(A「かつ」Bというときには、図のように楕円で「かつ」の条件であることを示す。)
③原因結果の間にまだ論理的関係が十分でない場合には、さらにUDEを書き加えていく。 たとえば、『社員教育制度が貧弱』だから『職務に必要な教育が十分に行われていない』
という中間のUDEを加えることができる。
④ツリー構築の過程において、列挙されたUDEの中で適切でないものは除外する。どの UDEが適切で、どのUDEが適切でないかを発見することは結構難しいが、ツリーの 中の因果関係に入れ込めないものは除外すると考えてもよい。
- UDEの根本となるUDEを特定し「根本問題(RC)」とする
それを解消すれば多くのUDEが解消するRCを「中核問題(CP)」とする。
問題構造ツリー
現状問題構造ツリー
現状問題構造ツリーで中核問題(CP)を発見すれば、その中核問題を解決すればよい。し かし、中核問題が見つかることは、必ずしもその解決策が見つかるということを意味しない。
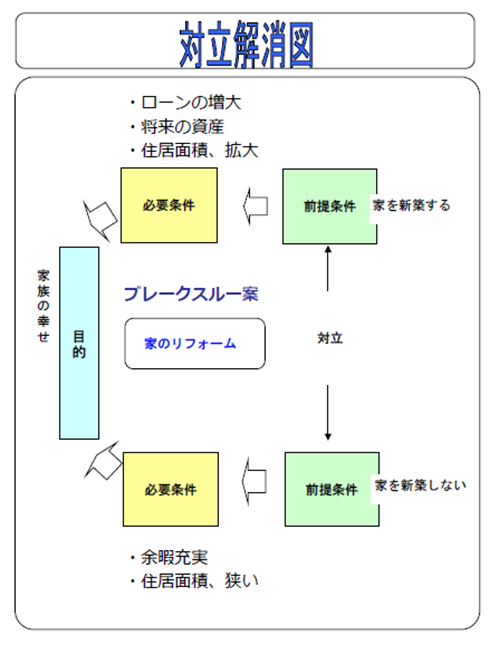
このような場合にTOCでは、「対立解消図」を利用する。対立解消図は別名「雲」と呼ばれる こともある(正確には蒸発する雲(Evaporating Cloud)) 中核問題であるUDEを反対にしたものが解決された状態ということになり、それを導く方 法が解決策である。直感的に解決策が分かる問題もあるが、対立解消図が活躍するのは、その 解決策が相対立する場合である。
対立解消図の仕組みは、図にあるように、①「目的」、②目的を達成するための「必要条件」、③必要条件が成り立つための「前提条件」という構造だ。必要条件どうしは対立しないが、前 提条件が対立する場合には、その対立を前提としながらも、目的を達成する方法(ブレークス ルー案)を考えることになる。
まず、どういう状況で問題点が対立しているのかを直感的に分かるための手段である。対立 解消図が書けたからといって、必ずしもブレークスルー案を考えられるとは限らないが、現状 把握の前提図だと考えればよい。
現状問題構造ツリー
未来問題構造ツリー
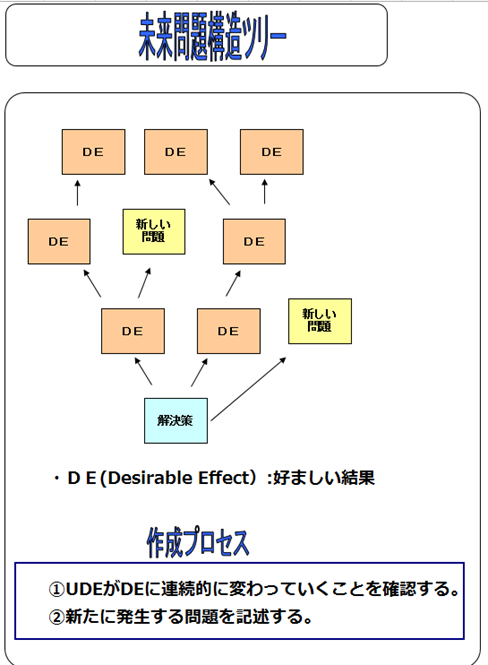
対立構造図などを用いて解決策を見出した場合に、それをもとにして新たな問題が発生しな いかどうかを検証するためのツリーを「未来問題構造ツリー(Future Reality Tree)」という。
現状問題構造ツリーの中核問題を解決する解決策を現状問題構造ツリーに組み込み、UDEが DE(Desirable Effect:一好ましい結果)となっていくかどうかを検証することもできる。
未来問題構造ツリーを構築する場合に注意すべきなのは以下の点である。
①現状問題構造ツリーで発見した中核問題の解決策を組み込んだ場合に、UDEがDEに 連続的に変わっていくことを確認する。特に、最終的な目的となる(現状問題構造ツリ ー上の上位に位置づけられる)UDEがDEに変わることが重要である。さもなければ、 重要でない現象(UDE)が解消されても、求める結果が出ないということにもなりか ねない。その場合には、現状問題構造ツリーのロジックを再度チェックする必要がある。
すべてのUDEが解消しない場合には、解消されないUDEが重要な問題であるかどう かも確認する。
②新たに発生する問題を記述する。解決策を組み入れることによって発生する可能性のあ る問題を記述する。問題解決策を発見した場合には、その良い面だけに着目して悪い面 が見過ごされがちとなる。新たに発生する可能性のある問題(UDE)を未来問題構造 ツリーの中に組み入れていき、それが重大な問題とならないかどうかの検証をすることが 必要となる。
未来問題構造ツリー
前提条件ツリー
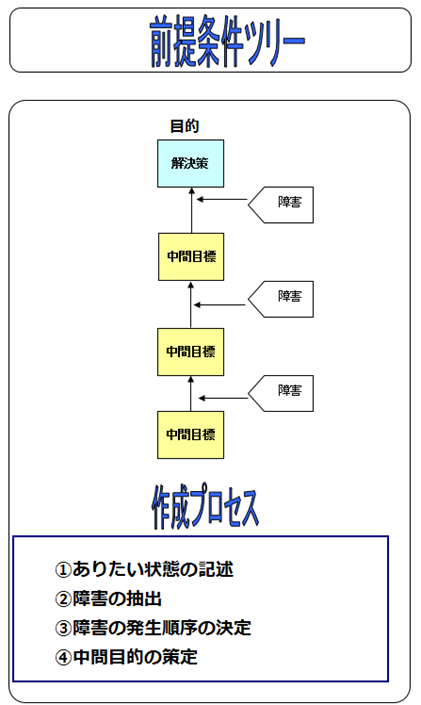
「前捉条件ツリー(Prerequisite Tree)は、解決策などのアイデアを実行するうえで発生するであろう「障害」とそれを克服すれば達成しうる「中間目的」を記述していくツリーだ。さらに、 このツリーは目的達成のための実行計画の前提ともなる。
このツリーは一番上に「ありたい状態」を記述する。これは、中核問題解決のための解決策で もよいし、副次的な問題を解決するためのものでもよい。そしてそのありたい状態を前提とし て、この状態を達成するためにはどのような「障害」が発生し、それを克服した状態:「中間目 的」がどのような順序で必要かということをツリーに記述していく。考えられる障害とそれが 解決した中間目的をすべて記述していく。記述の方法としては、①ありたい状態の記述、②障害 の抽出、③障害の発生順序の決定、④中問目的の策定、という順序になる。
前提条件ツリー作成にあたっては、これが実行計画の前提となるために、下のほうから順に クリアすべき障害と中間目的を並べていくこととなる。
前提条件ツリー
移行ツリー
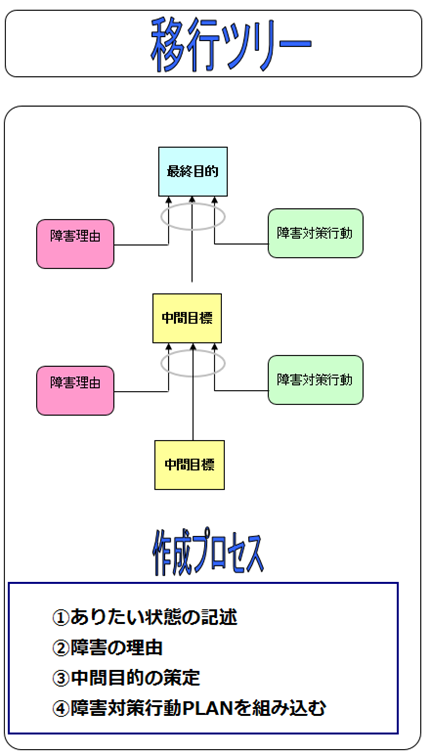
移行ツリー(Transion Tree)は、前提条件ツリーに障害克服方法を組み入れたツリーだ。ありたい状態を達成するために発生する障害の克服方法を前提条件ツリーに組み入れることによ り、ブレークスルー案の具体的な実行計画が完成する。
①ありたい状態の記述
②障害の理由
- 中問目的の策定
-
障害対策行動PLANを組み込む

移行ツリー
■参考文献
『図解TOC・スループット経営』 著者:小宮 一慶 東洋経済印刷
『制約理論(TOC)についてのノート』 著者:小林 英三 ラッセル社




















コメント