2024年版　わかりやすい　マトリックス・データ解析法(主成分分析)【イラスト図解】

マトリックス・データ解析法の作り方について下記の点をポイントに図解入れで解説しています。

マトリックス・データ解析法　 エクセル
マトリックス・データ解析法の活用例

モノづくりの参考になれば幸いです。(*^_^*)

 

2024年版　　分かり易い　マトリックス・データ解析法の作成　【音声解説付き】

QC検定3級の「品質管理の手法 新QC七つ道具のひとつである「マトリックス・データ解析法」の動画紹介。

3分で分かる！　マトリックス・データ解析法とは　概要解説

マトリックス・データ解析法とは？

マトリックス・データ解析法は、複数のデータをマトリックス（表）形式に整理し、その間の関係性やパターンを視覚的に捉え、問題の解決や意思決定に役立てるための手法です。

• 特徴:

  • 多様なデータに対応: 数値データだけでなく、文字データやカテゴリーデータなど、様々な種類のデータを扱えます。
  • 複雑な関係性を可視化: 複数の変数間の関係性を一度に把握しやすく、複雑な問題をシンプルに整理できます。
  • 客観的な分析: 主観的な判断を減らし、より客観的な分析が可能になります。
  • 問題解決の糸口発見: データ間の関連性から、問題の原因や改善点を見つけ出すことができます。

• 具体的な活用場面:

  • 品質管理: 製品不良の原因究明、工程改善
  • マーケティング: 顧客セグメンテーション、新製品開発
  • 経営戦略: SWOT分析、リスク評価
  • その他: 人事評価、アンケート分析など

マトリックス・データ解析法の手順

1. データ収集: 分析したいデータを収集します。
2. マトリックスの作成: データをマトリックス形式に整理します。
3. データの集計: マトリックス内のデータを集計し、必要な情報を抽出します。
4. 分析: 集計結果から、データ間の関係性やパターンを分析します。
5. 考察: 分析結果から、問題点や改善点、今後の施策などを検討します。

マトリックス・データ解析法の種類

• 単純マトリックス: 2つの変数の関係性を表す最も基本的なマトリックスです。
• 多重マトリックス: 3つ以上の変数の関係性を表すマトリックスです。
• 相関マトリックス: 変数間の相関関係を表すマトリックスです。
• 重要度マトリックス: 各要素の重要度を数値化し、マトリックスに表示する手法です。

マトリックス・データ解析法のメリット

• 直感的な理解: 視覚的にデータを見ることができるため、非専門家でも理解しやすい。
• 効率的な分析: 大量のデータを短時間で分析できる。
• 問題点の早期発見: 問題点を早期に発見し、対策を講じることができる。

マトリックス・データ解析法のデメリット

• データの質に依存: データの質が低い場合、分析結果の信頼性も低くなる。
• 主観的な要素が含まれる可能性: 分析者の解釈によって、結果が異なる可能性がある。

 

マトリックス・データ解析法とは

マトリックス図に配列された多くの数値データを見通しよく整理する方法．新QC七つ道具の一つ.

Ｌ型マトリックスの各交点に数値データが配列されている場合に，それらのデータ間の相関関係を手
がかりにして，それらのデータのもつ情報を一度になるべく多く表現できるような数個の代表特性を求めることにより，全体を見通しよく整理する方法である．

この方法は，主成分分析と呼ばれる多変量解析法の一手法で，新ＱＣ七つ道具の中で唯一の数値データ解析法である.

関連用語：主成分分析

引用先：クォリティーマネジメント用語辞典　日本規格協会

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

マトリックス・データ解析法とは、マトリックス図の交点に数値データが与えられた場合に多くの数値データを相関分析などで処理し、二次元平面図（Ｘ－Ｙ平面図）に表わし、問題とその要因との関係をわかりやすく示す手法です。

英語：matrix data analysis　　　　　　　中国語：矩阵数据分析法

ビッグデータで使用される多変量解析では主成分分析といわれ原石(データ)をダイヤ(活きた情報)に変えることができます。

競合分析、自社・他社分析、5択式アンケートなど、市場調査結果から売れ筋を見極めて新商品開発の方向性を選択するといった場面などに使用することができます。

英語：Principal component analysis

マトリックスデータ解析法の特徴

マトリックス・データ解析法は、膨大なデータの中から重要な情報を取り出し、データを簡潔にまとめることができるため、ビッグデータ解析や品質管理、 マーケティング、AI解析など様々な分野で活用されています。

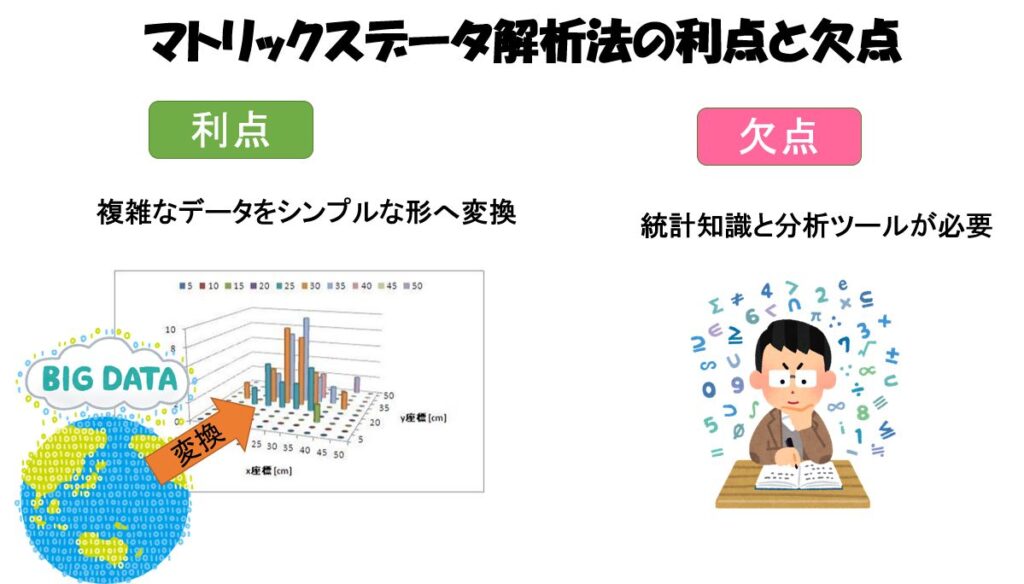
マトリックスデータ解析法の利点

①マトリックスデータ解析法は複雑なデータをシンプルな形へ変換できます。

マトリックスデータ解析法を用いれば、膨大なデータであってもグラフや散布図の形で表現でき視認性も高まりデータから何が言えるか、改善のためには何ができるのかといった議論を活性化させるに有効なツールです。

②情報処理リソースの節約が可能

膨大なデータの処理はそれだけで多くの時間と労力を要します。マトリックスデータ解析法によって処理に要する人的、あるいは機械的なリソースを節約でき、その利点はデータが多ければ多いほど大きくなります。

マトリックスデータ解析法の欠点

①高度な知識と分析ツールが必要

マトリックスデータ解析法の実施には高度な統計学の知識が必要です、そのデータがどのようにして生まれ、どのような意味を持つかを説明するには、その処理の工程を具体的にイメージできなければなりません。したがってマトリックスデータ解析法は、新QC7つ道具の中でも難易度が高く、実施が難しい手法であます。

 

マトリックス・データ解析法の目的

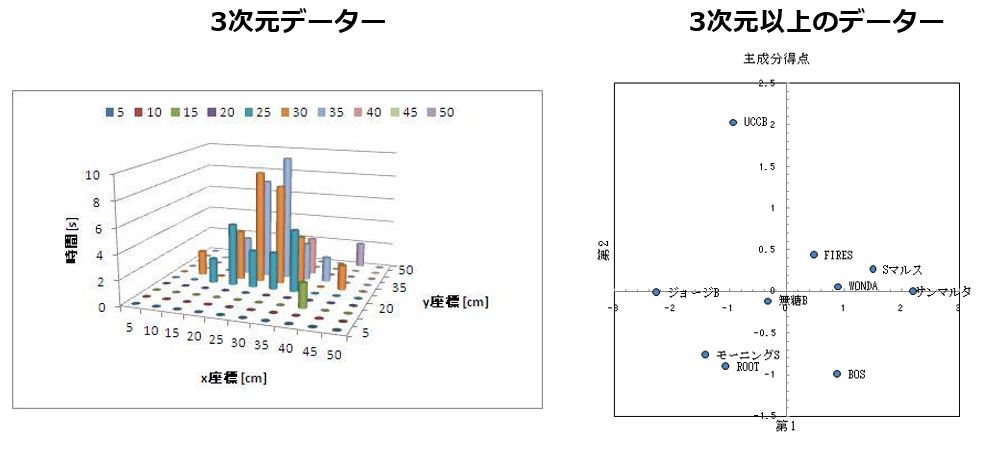
次元削減でデータをシンプルに

3次元までのデータであれば立体図（X,Y,Z)で表現すれば視覚的にも傾向を把握しやすくなりますが3次元以上のデーターの場合は立体図（X,Y,Z)は使用できないのでの3次元以上のデーターの次元数を削減する手法として主成分分析が用いられます。

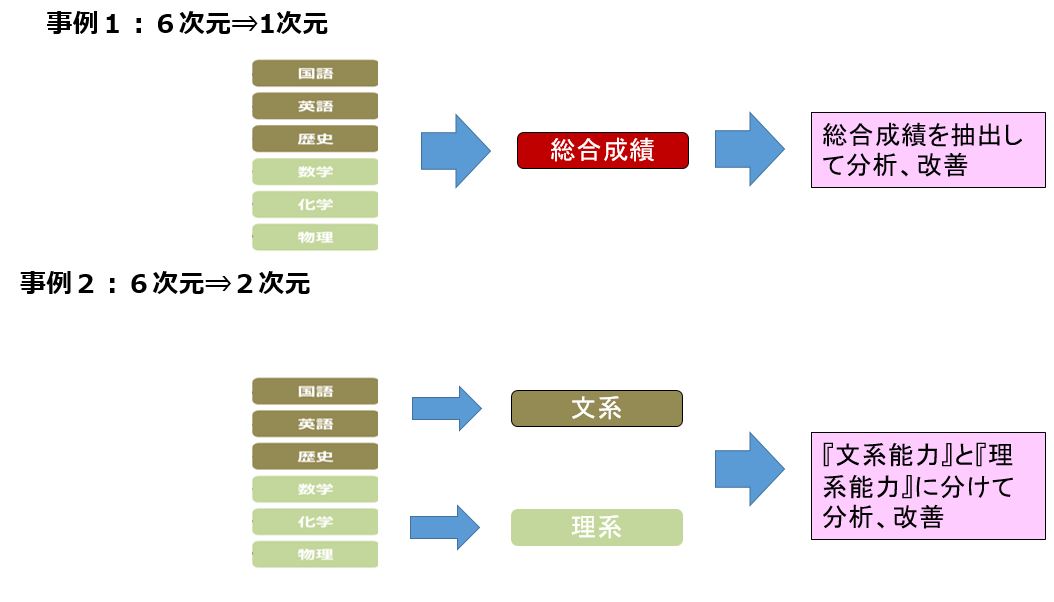
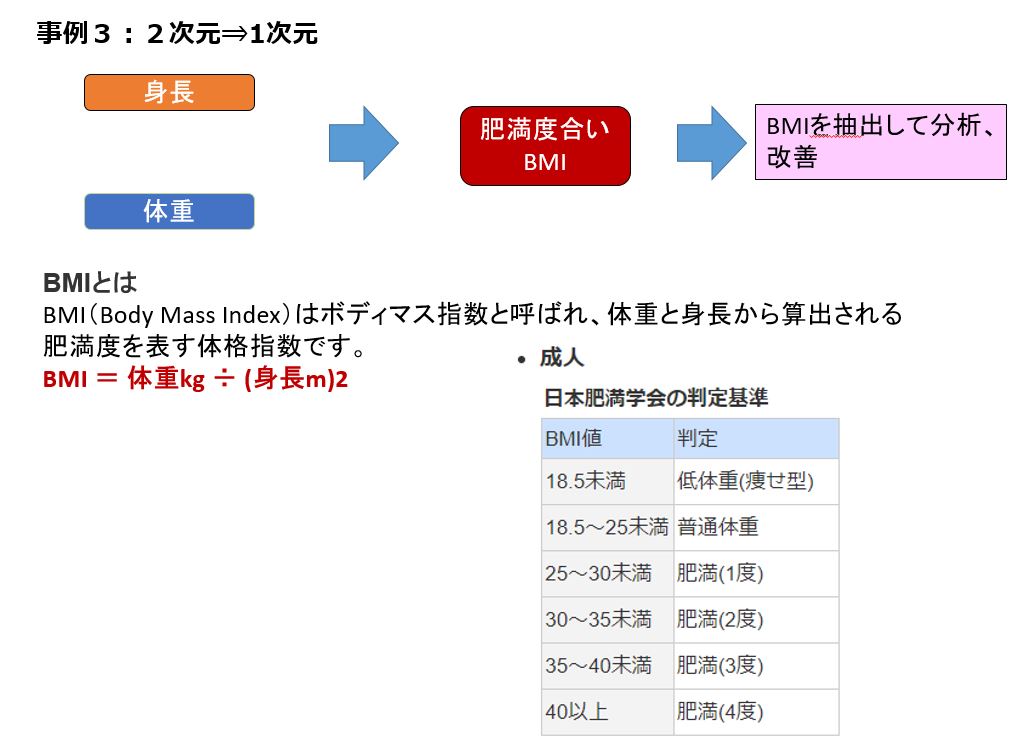
マトリックス・データ解析法（主成分分析）とは、多くの変数を持つデータについてできるだけ情報量を落とさずに、その特性をより少ない次元で明らかにする手法のことです。例えば、次に3 つの例を示します。

マトリックス・データ解析法で陳列棚を改善

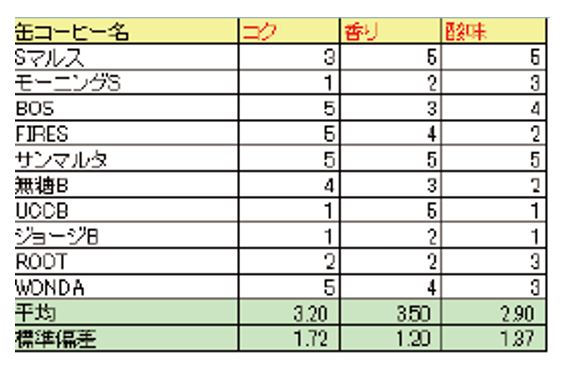
アンケート結果をもとに、缶コーヒーの陳列方法を検討。

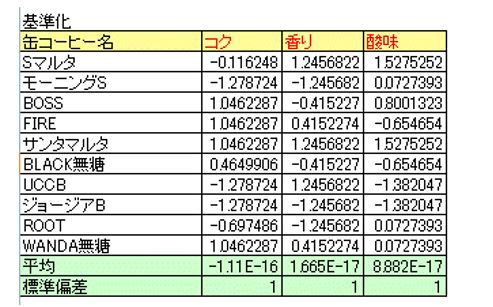
各缶コーヒーについて、「コク」「香り」「酸味」の3つの特色で5段階評価のアンケートをとりました。以下の表は、各缶コーヒーの評価点と平均、標準偏差をまとめています。

目的は缶コーヒーの陳列をお客様の要望に合わせて売り上げを増加させることです。

①消費者の立場に立って人気商品を評価⇒例：総合的な人気商品で評価

②特化した個性で訴求する商品で評価⇒例：「香りにこだわる人へ」

 

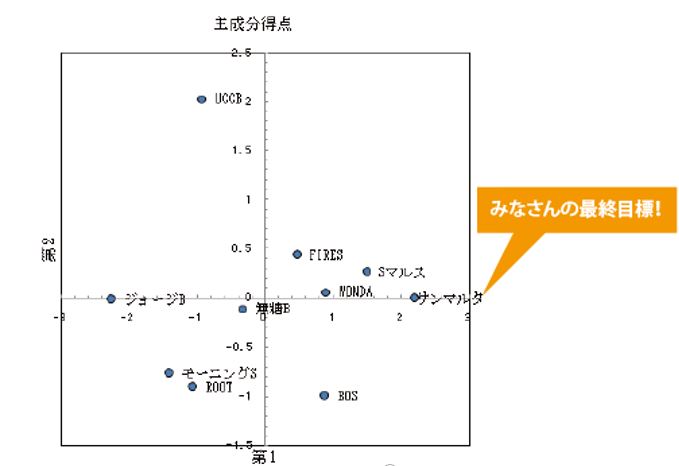
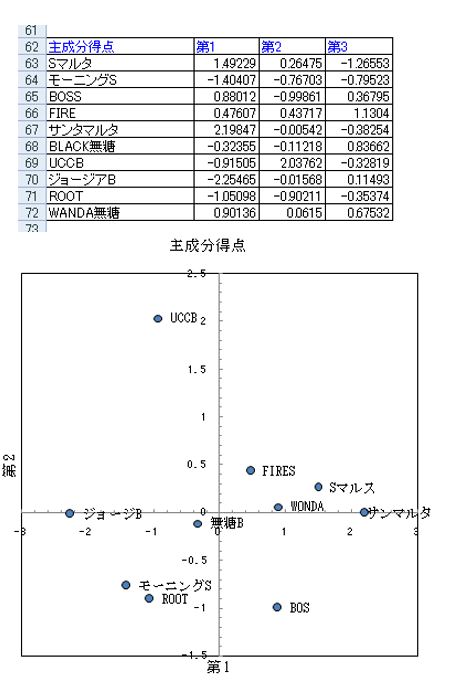
アンケート結果を散布図で視覚化

次の散布図は、とりあえず計算結果を省いて、主成分分析の最終出力結果

を視覚化したものです。縦軸は「香り」、横軸は「総合力」を表しています。

図から、たとえば次のことがわかります。総合的に1番人気なのは、「サンマルタ」、総合評価では低いが、「香り」に特色があるのが「UCCB」といった具合です。

缶コーヒーの陳列棚　改善

お客様が商品を選ぶときの参考にライスカードの横にチラシをつけて販売することにしました。

「とりあえず迷ったらこれ！」サンタマルタ……総合的な人気商品

「香りにこだわる人にはこれ！」UCCB……香りに特化した個性で訴求

 

マトリックス・データ解析法の手順、全5ステップ

1.変数の単位を揃えるためにデータを基準化する

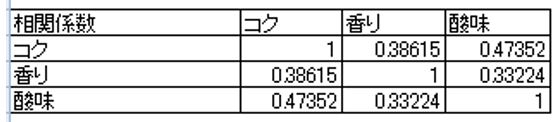
2.基準化したデータの相関係数行列を求める

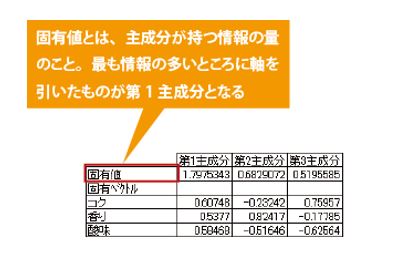
3.相関係数行列の固有値を固有ベクトルを求める

4.分析結果の精度を確かめる

5.主成分得点を求め、散布図を描く

 

 

 

 

 

＊具体的なエクセルを用いたマトリックス・データ解析法は下記のサイトにて分かりやすく解説しているのでそちらを参照してください。

①平均点が違う国語／化学のテスト80点を評価するには？　Excel関数「STANDARDIZE」でデータを基準化しよう

②コーヒーの「コク」「香り」「酸味」のデータから新たな評価軸を生み出すには？　Excelで相関係数行列、固有値と固有ベクトルを求める

③缶コーヒー総合力1位はどれだ？「コク」「香り」「酸味」の主成分得点を求め、散布図を描いて解釈する

 

マトリックス・データ解析法の作り方　事例

目的を決定

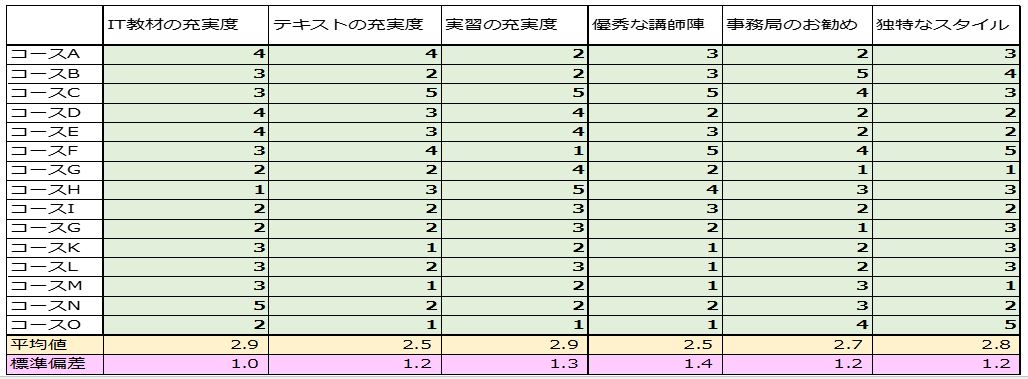
全社的に実施しているセミナー15コースを、｢IT教材の充実｣からはじまって、｢独特なスタイル｣まで６つの評価尺度で評価し、どういったセミナーがよいのかを探つてみることにしました。

評価は、５段階評価で｢５｣に近いほどよい評価点とします。この評価にあわせてセミナーごとの受講希望者の動向も５段階で評価することにしました。

【評価の概要】
評価セミナー数：１５コース
評価項目：｢IT教材の充実度｣｢テキストの充実度｣｢実習の充実度｣｢優秀な講師陣｣
｢事務局のお勧め｣｢独特なスタイル｣
結果評価：｢受講者数の増加状況｣
評価点:５点：非常によい　４点：よい　３点：普通　２点：悪い　１点：非常に悪い

 

マトリックス・データ収集

目的に合わせて、データを収集します。
収集するデータは、アンケート形式でも実測値でもかまいません。数値データであれば解析できます。　マトリックス・データ解析に必要なデータは、各サンプルにすべての評価点が入ってていることが必要条件です。

したがって、アンケートなどからデータを収集するときは、すべての項目に何らかの評価点が記入されるよう注意しておきます。

ここでは、１５コースのセミナーを評価した結果をマトリックス・データ形式にまとめています。行にサンプルナンバーを記入し、列に評価項目をタイトルとして記入します。
記入が終われば、欠落データがないか､誤記入がないかなどをチェックします。

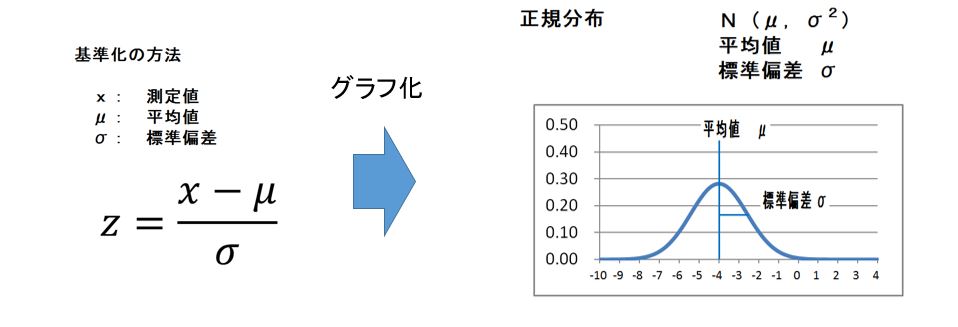
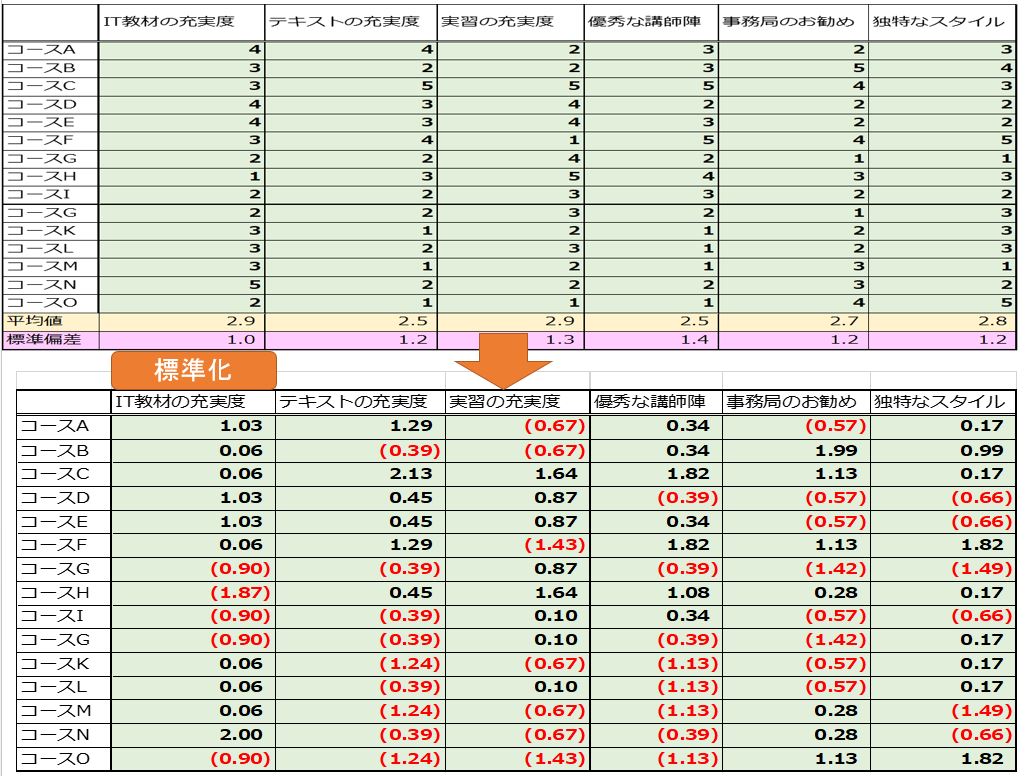
データーを基準化

ここでのデータは、すべて項目の評価点の大きさと単位が同じですが、評価項目が身長、体重、年齢など大きさや単位が違う場合､単位の取り方によって、答えが変わります。

そのため、各データを平均値０、標準偏差１のデータに変換することで、この問題を解消することができます。この方法をデータの基準化といいます。

基準化データは、次の式で計算します。
基準化デー夕＝(デー夕)ー(平均値)/(標準偏差)
例えば、コースＡの｢IT教材の充実｣の基準化データは

｢IT教材の充実｣の基準化データ＝　４－２.９３３/１.０３３＝1.０３３

となります。

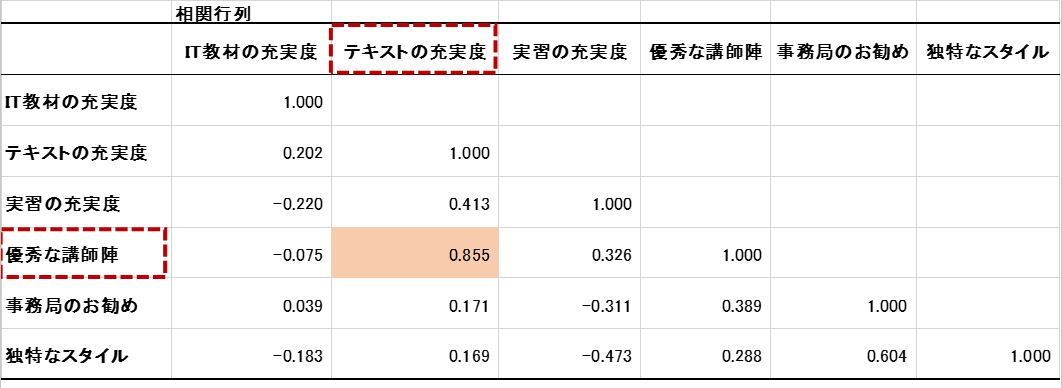
相関係数を計算

相関係数とは、２つの項目間に関係があるかどうかを評価する係数です。

相関係数は、－１から＋1までの値をとり、±1に近いほど相関があるといい、この相関が強い項目を１つにまとめることがマトリックス・データ解析法の特徴です。

｢テキストの充実度｣と｢優秀な講師陣｣の２つの項目の相関係数は０.855であり、＋1に近いため相関が強いということがわかります。

以下､｢事務局のお勧め｣とF独特なスタイル｣の相関係数が０.６０４、｢テキストの充実度｣と｢実習の充実度｣の相関係数が０.４２３と続いています。
この相関係数の一覧表をここで示します。これを相関行列とよびます。相関行列を計算するには、エクセル分析ッールの｢相関｣を利用します。

主成分を選ぶ

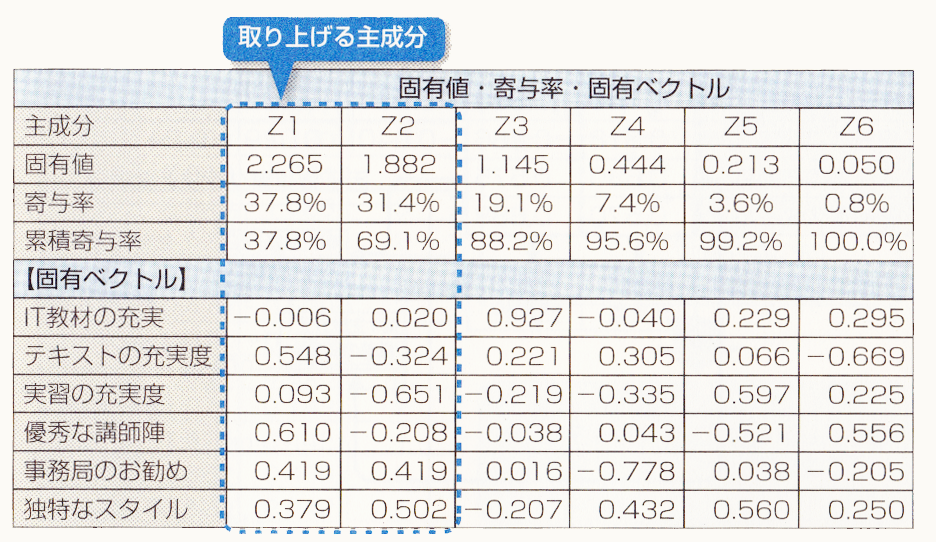
固有値とは、新しい評価尺度(主成分)それぞれが、全体の情報量(ばらつきの大きさ)のうち、どれくらいパーセントを占めているかを表しています。

例えば、この表の新しい１番目の主成分Z1は、全体の情報量の３７.８％(固有値二主成分の数、２.２６５丁６)となります。これを寄与率といい、１つの主成分が元の全項目が持っている情報の何割を説明できるかを表しています。第１主成分Z1と第２主成分Ｚ２の寄与率を足した６９.1％を累積寄与率といいます。

主成分をいくつ採用するかは､累積寄与率が７０～８０％以上で、固有値が｜以上ということが目安になります。ここでは、第１主成分ZI(固有値２.２６５)と第２主成分Ｚ２(固有値1.８８２)を取り上げることにします。この２つで、累積寄与率が６９.1％であり、ほぼ７０％をクリアしています。

固有ベクトルの計算は、エクセル2010のソルバー機能を利用して計算することができます。

 

 

 

 

 

 

 

 

 

主成分のネーミング

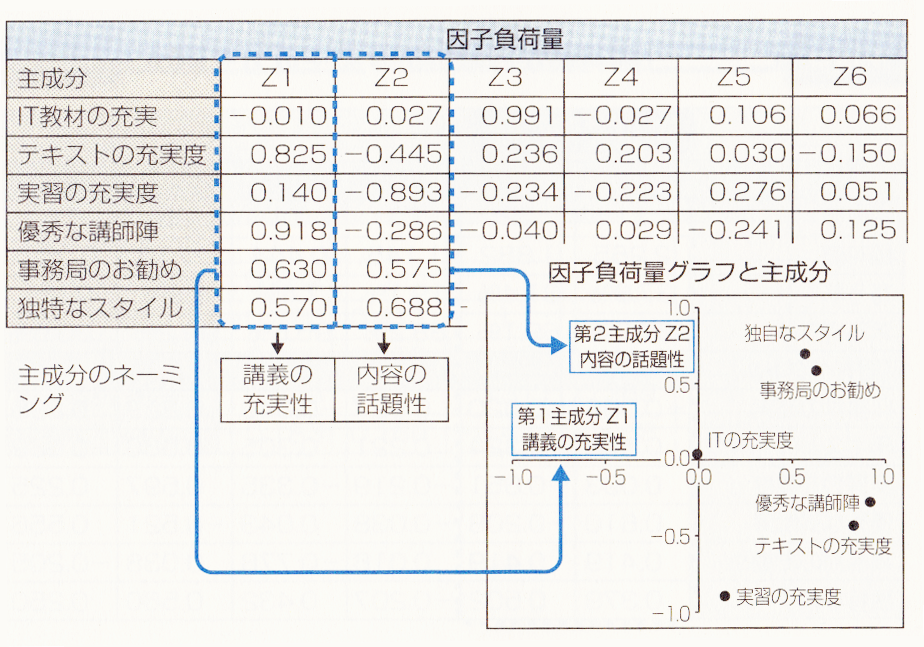
各主成分と元の評価尺度(IT教材の充実など６項目)との相関係数を計算したものを因子負荷量といいます。この値は各主成分が元の評価尺度とどれくらい強く関わっているかを示すものです。

新たに取り上げた第１主成分Z1と第２主成分Ｚ２のネーミングを行います。主成分のネーミングは、｢主観的に｣行われますが、その際、手がかりとなるのは、主成分を構成している固有ベクトルや因子負荷量の大きさと符号です。

例えば、第１主成分Z1は、ほば６項目とも｢十｣の値を示しており、これを｢講義の充実性｣とネーミングします。同様に第２主成分Ｚ２は、｢テキストの充実度｣｢実習の充実度｣と｢優秀な講師陣｣が｢－｣であり、｢IT教材の充実｣｢事務局のお勧め｣と｢独特なスタイル｣が｢十｣であることから、これを｢内容の話題性｣とネーミングします。

 

 

 

 

 

 

 

 

 

 

 

主成分得点の計算

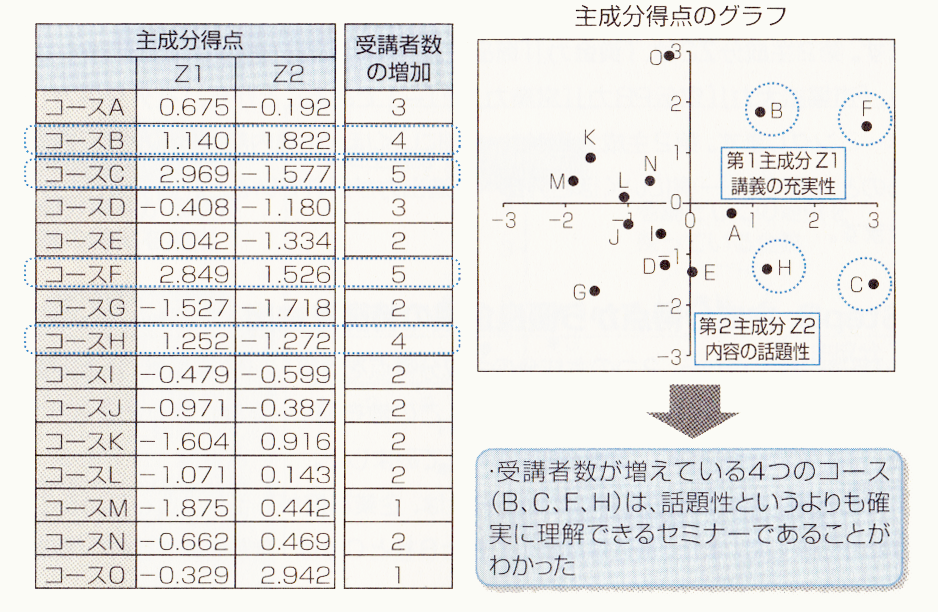
主成分の式を使つて対象的に(例えばコース別に)、主成分の値を算出したものが｢主成分得点｣です。
主成分得点は対象のグルーブ分けや対象の評価に使います。グルーブ分けの際に役立つものは主成分同士の散布図です。第２主成分まで採用するのであれば、第１主成分と第２主成分の散布図を作成し、視覚的にグルーブ分けを行います。

ここでは､第１主成分ｚ1｢講義の充実性｣と第２主成分ｚ２｢内容の話題性｣の散布図を書き、別データから｢受講者数が増えてきているコース｣をマーキングすると、４つのコース(Ｂ、C､F、Ｈ)は、話題性というよりも確実に理解できるセミナーであることがわかります。

マトリックス・データ解析は、このようにして視覚に訴えられなかった多次元データを情報の損失をできる限り少なくして、２次元で考祭することができます。

 

 

 

 

 

 

 

まとめ

マトリックス・データ解析法は、様々な分野で活用できる強力な分析手法です。複雑なデータを整理し、問題解決の糸口を見つけるために、ぜひ活用してみてください。

関連キーワード：

＃マトリックスデータ解析法事例

＃マトリックスデータ解析法 Excel

＃マトリックスデータ解析法 R

 

slideshare 　無料ダウンロード資料（PDF)

パワーポイントで作成した資料です。無料ダウンロードOKです。

 

おすすめ　新QC七つ道具　　参考文献

新QC七つ道具の基本と活用 (はじめて学ぶシリーズ) 猪原 正守 (著)

図解入門ビジネス新QC七つ道具の使い方がよ~くわかる本　今里 健一郎 (著)

よくわかる「新QC七つ道具」の本 (ナットク現場改善シリーズ) 鈴木 宣二 (著)

【アマゾン　おすすめ本　新ＱＣ七つ道具】