サーミスタの選び方、使い方、不良モード、用途、応用製品

 

【アマゾン　おすすめ本　サーミスタ】

サーミスタを理解する為に下記の本がお勧めです。こちらから

サーミスタとは？　英語：thermistor

サーミスタとは、温度を測定する為のセンサー（検出器）です、熱に敏感な反応する抵抗体を使用し、温度の変化につれてその抵抗値検知して温度を即てする半導体素子です。

スマートホンの加熱防止センサー、冷蔵庫、エアコンの温度制御としてのセンサーとして色々な製品に使用されています。

 

サーミスタの名称は温度に敏感な抵抗体(Thermally Sensitive Resistor)から名付けられた名称といわれている。

 

 

 

 

 

 

サーミスタの歴史

最初のサーミスタ（NTC型）は1833年、硫化銀の半導体を研究していたマイケル・ファラデーによって発見されました。ファラデーは、硫化銀の抵抗が温度が上昇するにつれて急激に減少することに気づき、サーミスタを発見しました。

 

 

 

 

 

 

 

但し、初期のサーミスタは製造が困難であり、この技術の用途が限定されていたため、サーミスタの商業生産は1930年代からです、商業的に実際に使用できるサーミスタはSamuel Rubenによって1930年に発明されました。

 

サーミスタの原理　～抵抗率が変化する理由～

NTCサーミスタの材料はマンガン (Mn) 、ニッケル (Ni) 、コバルト (Co) などを成分とする酸化物を焼成したセラミックスであり、半導体です。

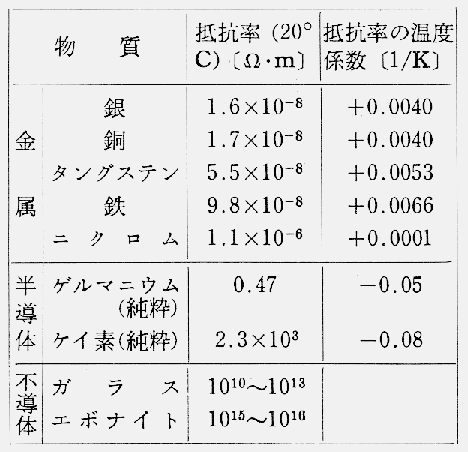
普通の金属、導体では，温度が上がると抵抗が増す(α＞o)。これは，金属結晶を構成する陽イオンの熱運動による振動の振幅が大きくなり，そのため，自由電子との衝突回数が多くなり，自由電子の平均移動速度が小さくなるからである。

これに対して，半導体では，電荷の運び手である自由電子やホールの増加する割合が，それらの移動速度が小さくなる割合よりも大きいので，温度が上がると抵抗は小さくなる(α< 0)。

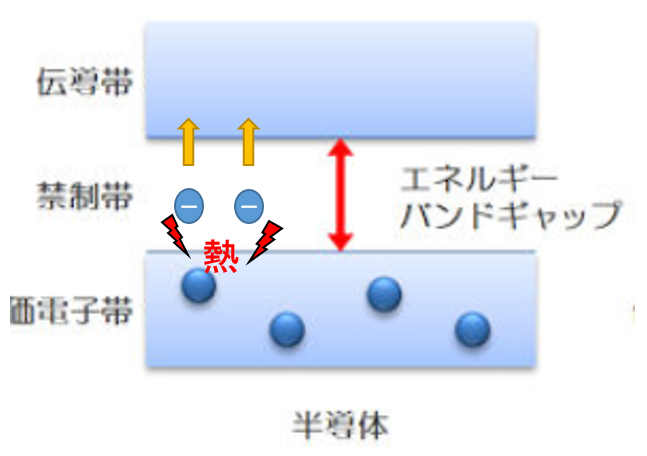
半導体は小さなエネルギーバンドギャップを持つため、外部からエネルギーを供給されない状態では、価電子帯の電子は伝導帯へ移動することができず、電気抵抗の大きな状態となります。
一方、外部からエネルギー（熱、光等）を与えられると、価電子帯の電子はそのエネルギーを得て伝導体へ移動し電気を通すことができるようになります。

これが、温度が上昇すると電気抵抗が下がる理由です。

 

 

 

 

 

 

 

公式：導体の0℃における抵抗をR０[Ω]とするとｔ[℃]における抵抗R〔ｎ〕は下記の式であらわせます。
R = R0( 1十αt)

 

 

 

 

 

 

 

 

抵抗の温度による変化を利用して，電流の強さによって温度を測定するものを抵抗温度計という。　白金抵抗温度計はその代表的なものである。これは測定範囲が広く(-260°～1600°Ｃ)，特に　-180°Ｃ～30°Ｃの範囲では，標準温度計に用いられるほど精密な温度測定に適する。
また，最近，半導体の抵抗の温度変化を利用したサーミスター温度計がよく用いられる。これは小型で温度係数が大きいので，敏感である。

 

サーミスターの種類

また、サーミスタは数種類あるが主なものはつぎの２つです。

ひとつは温度が高くなるのにしたがってその抵抗が低くなる負の温度係数　(Negative Temperature Coefficient)を持ったＮＴＣサーミスタ。

ふたつめは温度が高くなるとある温度で急激にその抵抗が高くなるPTC (Positive Temperature　Coefficient)サーミスタである。

半導体セラミックスは身近な製品に利用されています。電子体温計などの温度センサに使われるのはNTCサーミスタというタイプ。セラミックファンヒータなどに用いられるのはPTCサーミスタというタイプです。

NTCサーミスタは、温度変化に対して抵抗値が3～5%/℃と変化します。一般的な温度センサとして多くの電子機器に使用されています。

PTCサーミスタは、電流を流すと電気抵抗によりジュール熱が発生して温度上昇しますが、一定温度となると急激に抵抗値が増えて電流を流しにくくします。このため電圧が一定ならば、一定の温度を保つ発熱体となります。スイッチを入れると、たちどころに発熱して熱風を送ってくれるのは、PTCサーミスタを利用したセラミックヒータならではの便利さ。また、一定温度以上に発熱しないので火災などの心配もなく、ふとん乾燥機などにも利用されています。

何故、サーミスターが温度センサーとして使われるのか？

現在はマイコン化されたさまざまの機器が家庭、工場に使用されています。

その機能を生かし目的を果たすためには，マイコンに質のよい信号を供給するセンサが必要とであり、サーミスタが多くの温度センサの中で最もこの目的に合っていたからというのが，今日のようにサーミスタが多く使われるようになった理由です。

昔は温度は棒状のガラス温度計で読まれ，バイメタルの温度接点付きのもの，あるいは液膨式の温度調節器などによって機器が制御されてきました、したがって，十分な精度を期待することはできませんでした。

しかし、トランジスタが発明され，電子回路がプリント配線板の使用などで次第に小型化され，やがて　ＯＰアンプが普及してきて，回路の機能にふさわしいセンサへの要求が高くなったとき，それらでは電気信号をとり出すことが難かしかった。そのような中にあって温度センサをもう一度見渡してみると，白金測温抵抗体は高価なことに加えて，その抵抗値が低く温度係数が小さいので，太い導線を使ってセンサ回路の線の引きまわしをしなければならないこと，精度を上げるためには３線式の結線をしなけれぼならないため，計装の費用か嵩むこと，センサの形状に自由度が低く小型化しにくいこと（したがって応答が悪い）などの欠点がある。

熱電対はアップ回路が小型化されて使い易くはなったが，基準接点の自動補償回路が必要であり，自動補償回路自体も誤差をもっていること，センサは小型で加工し易いが場合によっては補償導線を使う必要があることなど，いろいろ問題になる点が多い。

これに対してサーミスタの場合には小型で加工性がすぐれていること，素子の抵抗が高く，しかも抵抗の温度係数が大きいので1 °Cの温度変化に対する抵抗変化量が大きくなるため，細い線でセンサの引きまわしができ，信号のレベルが高いので電子回路が簡単なものとなり価格が安い，分解能がすぐれているなど数々の有利な点が挙げられる。

 

 

 

 

 

 

 

 

 

 

 

 

 

サーミスタの選び方

サーミスタは白金測温抵抗体や熱電対と同様に重要な測温素子であり，主として民生機器，OA機器の分野で使われているが，工業計器の分野のものについてはJIS C 1611 サーミスタ測温体53)の規格の中で規定されている。

また，サーミスタ全般についてはJIS C 2570直熱形ＮＴＣサーミスタ通則、JIS C 2571 直熱形ＮＴＣサーミスタ試験方法よって規定されている。また，主としてサーミスタが使われている電子体温計などについては，JIS T 1140電子体温計JIS T 1306電子体温モニタがある。

下記のJIS規格を参考に最適なサーミスタを選択して下さい。

サーミスタ　JISC日本工業標準調査会サイト

サーミスタの日本工業規格はJIS C 1611です。JISC日本工業標準調査会サイト内のＪＩＳ検索から内容が閲覧可能です。（但し印刷不可、閲覧のみ）

＊現在はＩＥインターネット エクスプローラーのみ閲覧可。

kikakurui.com　｜JIS規格票をHTML化したサイト

サーミスタの日本工業規格はJIS C 1611です。全文、閲覧、印刷可能です。（但し図、イラスト含まず）

サーミスタ測温体　JIS C 1611

次にＮＴＣサーミスタを例にサーミスタの特性と諸定数します。

サーミスタの特性と諸定数

ＮＴＣサーミスタ(thermistor)はNi（ニッケル), Mn (マンガン），Ｃｏ（コバルト）などの遷移金属の酸化物の粉体をある割合で混合したものを，成型，焼結して作られる酸化物半導体である。

温度が高いときには抵抗が低く良く電流を流すが，温度が低いときには抵抗が非常に高く電流をほとんど流さない，温度で抵抗が変化する半導体である。

バリスタは電圧が高いと抵抗が低くなり，電圧が低いと抵抗が高くなる半導体であるが，半導体にはバリスタやサーミスタのように均一な組織の塊状のまま半導体の性質を示すバルク型（Bulk：かたまり）と，ダイオードやトランジスタのように不純物成分か違う（Ｐ型，Ｎ型）２つの部分の接合面のところで半導体の性質を示す接合型半導体の２種類がある。上で述べたようにサーミスタやバリスタはバルク型の半導体である。

 

サーミスタの抵抗値Ｒ-温度t特性とＢ定数

バルク型半導体であるサーミスタの抵抗と温度の関係は，基本的にはつぎの式で表される。

R=R0＊expB＊（1/T－1/To）＊  （式１）
ここに　R：絶対温度T（Ｋ）におけるサーミスタの抵抗値
R0：絶対温度T0(Ｋ)におけるサーミスタの抵抗値
B：サーミスタ定数
注意：　絶対温度は摂氏の温度（℃）に273.15を加えたもので，単位記号はＫである
＊　R＝R0　eB(1/T-1/T0)と同じ意味である。
たとえば
0℃は273.15K　　　100℃は373.15K　　　200℃は473.15K　　となる。

サーミスタ定数Bは，サーミスタの材料の組成や作り方で決まる定数で，Bが大きいほど，温度変化に対する抵抗変化の割合が大きい。

芝浦電子のサーミスタの代表的製品の抵抗一温度特性(Ｒ-Ｔ特性)を下図示したが，実用的には摂氏（℃）の目盛をして使い易くしてあるので，温度目盛が非直線になっている。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

また、サーミスタ定数Bの具体的な求めかたは下記のとおりである。

[例　題]０℃で30kΩ，100°Cで１kΩのサーミスタがある。このサーミスタのBの値を計算せよ。つぎに求めたBの値を用いて，このサーミスタの50℃の抵抗を計算せよ。

〔解〕０℃は絶対温度で273.15K, 100℃は373.15Kだから

B＝(lnR-lnR0)÷((1/273.15+t)-(1/273.15+to))

＝(ln1-ln30)÷((1/273.15+100)-(1/273.15+to))

=3466.7(K)

Bの値が求まったので式１の関係を用いて50゜Cの抵抗値を計算してみる。

R = 30×exp（3466.7×(１/(273.1＋50)-(1/271.15))=4.210 KΩ

となり，50°Cでの抵抗値は4.210 kΩと求まる。しかし，実際のサーミスタの抵抗は，いろいろな理由でごくわずかではあるが上に凸な曲がりをもっているのに対して，この計算はこのグラフの座標の上では直線として取り扱っているため，計算値より若干高めになっているはずである。

 

サーミスタの抵抗値の温度係数（α）

サーミスタの抵抗の温度係数αとは，サーミスタの温度がごくわずか変化したときに生じる抵抗変化の大きさと温度変化の割合を，その時の温度におけるサーミスタの抵抗値で割った値である。すなわち，抵抗の温度係数αはつぎの式2で定義される。

温度係数α＝(1/R)*(dR/dT)　　　　　　　　　　　式２

サーミスタの特性式は式（1）であるから，これから温度係数αを計算すると

α=1÷R0×expB(1/T-1/T0)×R0expB(1/T-1/T0)×B×(－1/T²)

=－B/T²

この結果から，サーミスタの抵抗が変化する割合は，サーミスタ定数Bに比例し，絶対温度の２乗に反比例，かつ負の符号を有することを示している。このマイナスの符号はサーミスタの抵抗値が温度の上昇とともに減少することを示すものであり, NTC (Negative Temperature Coefficient)と呼ばれる理由はここにある。

式２の結果から明らかなように温度係数αはBと比例関係にあるが，絶対温度の平方に反比例するので，温度が高くなるとその値が小さくなる性質があり，サーミスタが白金測温抵抗体などと比較して温度係数が大きいという特長は，温度が高いところでは消滅する。すなわち，サーミスタが抵抗の変化率が大きいという特長を発揮するのは，比較的に温度が低い範囲ということができる。
1 °Ｃ当たり抵抗が変化する大きさは
ΔR=R×α　　　　　　　　　　　　　　　　　　　　　　　　(式３)

である。いまB=3400Kのサーミスタがあるとき，27℃（約300K)における抵抗の温度係数αは
α=3400 /(300)²=-0.037
となる。すなわち約3.8％となり，白金測温抵抗体の温度係数が約0.39%であることを考えると，サーミスタの抵抗の温度係数は白金抵抗の場合の約10倍である。しかし，このサーミスタを100°Ｃ（約373K)で使うとその温度係数は約2.44%と低くなる。

サーミスタの熱放散定数δ

サーミスタは抵抗体だから，サーミスタに電流が流れると当然サーミスタはエネルギーを消費し，ジュール熱Joule’s heat)を発生する。一般に抵抗値がRのとき，その抵抗体に電流Iが流れるとI²科×Rのエネルギーが消費される。そのとき，抵抗Rで消費される電力は, W=i²×R（Ｗ：ワット）である。ここで消費される電力は熱となるが，発生した熱はサーミスタのリード線を通して，あるいは周囲の物体を通しての伝導や対流，または輻射によってその一部が失われるが，発生した熱の一部はサーミスタの温度を上げる結果となり，電流を流し続けるとやがてある温度で平衡に達するようになる。

このようにしてサーミスタの温度が安定したとき，サーミスタに流れる電流をI mA, サーミスタの温度がt°Ｃ，サーミスタのそのときの抵抗がRkΩ，雰囲気の温度がta℃であるとすると次の式が成り立つ。

W=I²×R=δ(t一ta)（ｍＷ）　　　　　　　　　　　　　　　　　（式４）

ここに，δは熱放散定数(Thermal dissipation constant)と呼ばれる比例定数で，単位はｍＷ／℃である。　式から

δ＝W/（t-ta）＝I²×R/t-ta (mW/℃）　　　　　　　　　　　　（式５）

である。このδの値はセンサの構造，材質あるいは雰囲気の物質の種類や状態（比熱，熱容量あるいは流速など）によってさまざまであり，サーミスタを使った回路を設計するとき，求められる測定精度から，ジュール熱による誤差をどの程度まで認め得るかということにも関連して，回路に流れる電流を最大どれだけに抑えるかということに関わってくる。ｔ－ta= Δt (ジュール熱による温度上昇の大きさ）とすると

Δt = t―ta＝W/δ=I²×R/　（℃）　　　　　　　　　　　　  （式６）
であり，この式を使ってサーミスタに電流を流したときに発生する熱のために生じる温度上昇が計算できる。このΔtを一般には自己加熱（Ｓelf heating)と呼んでいる。自己加熱の大きさがΔt℃になるときの電流Iは自己加熱した状態でのサーミスタの抵抗値をRkΩとすると

　i＝　√(δ×Δt/R)　（ｍＡ）　　　　　　　　　　　　　　（式７）

で与えられる。温度上昇Δtが小さいときには，Rには通電前の値を用いてもよいがRは本来は，温度が上昇して平衡に達したときの抵抗値であることに注意しなければならない。

また，熱放散定数δ　mW/℃は，δｍＷの電力をサーミスタに消費させたとき，サーミスタの温度が１Cだけ温度上昇するといいかえることも可能である。

ちなみに，ガラス封入されたサーミスタの熱放散定数はラジアルタイプでは，大きさによって0.2～2mW/℃，アキシャルタイプで1.5～3mW/℃（いずれも静止空気中で）である。

 

サーミスタの（熱）時定数τ

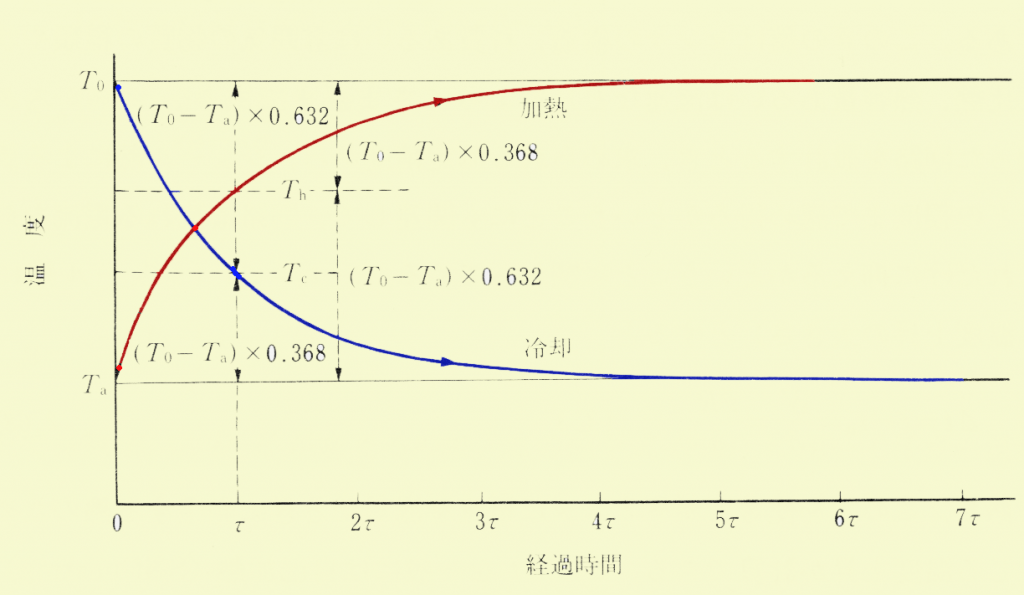
一般に温度センサにステップ状の急激な温度変化を与えたとき，センサの温度はゆっくりと変化してゆき，やがて最終の温度に到達する。その様子を下図に示す。加熱と書かれているカーブは，サーミスタを室温の状態から高温の状態に急激な変化をさせたとき，冷却とあるのは高温の状態におかれていたサーミスタを急に室温の状態に取り出した場合の，サーミスタの温度変化の様子を示している。

 

 

 

 

 

 

 

 

 

このとき，その温度の変化の速さをいい表すのに，応答，応答性あるいは時定数という言葉が用いられるが，応答や応答性というのが概念的な言葉であるのに対して，時定数は物理的表現であり，サーミスタの応答をいうとき，通常は時定数が用いられる。JIS C 1611 サーミスタ測温体では白金測温体や熱電対の規格と組になった産業用温度センサの規格である関係から，90％応答を用いている。

 

いま，サーミスタの熱容量をH，熱放散定数をδとし，温度T0°Cに保たれているサーミスタを，雰囲気温度Ta℃の中に急に取り出して冷却する場合を考えよう。任意の微小時間dｔの間にサーミスタの温度がdT℃下がったと考えると次の式が成り立つ

ーH×dT＝δ（T-Ta)dt　　　　　　　　　　　　　　　　　　（式８）

いま, H/δ=τとしてこの式を解くと，その解は
Tc一Ta= (To―Ta )exp〔－t/τ〕　　　　　　　　　　　　　（式９）
となり
Tc＝Ta十（To－Ta）ｅｘp（－t/τ）　　　　　　　　　　　　(式10)

と，ある時間経過したあとのサーミスタの温度を表すことができる（ここにTcとサフィックス(suffix) Cを付けたのは冷却中であることを示すためである）。　このτ（タウ）を一般に（熱）時定数(Thermal time constant)と呼びｔ＝τ（タウ）が成立するときには

Tc＝Ta十(To-Ta)×0.368=Ta十（T0-Ta)（1－0.632）　　　（式１１）

と書くことができる。このTcの温度は始めの温度差（T0一Ta）の63.2%温度が下がったところの温度である。

Ta℃の雰囲気中にあって温度がTa℃であったサーミスタをT0℃での高温の中に急に入れるときには，サーミスタが外部から熱を得ることになるので，温度上昇中の温度をTで示すと

HdT=δ(T一Ta)dt　　　　　　　　　　　　　　　　　　　　　(式１２）

より，温度差の63.2%変化したときの温度をThとすると
Th＝Ta十(T0一Ta)×0．632　　　　　　　　　　　　　　　　(式１３）

が得られる。以上の関係から時定数はサーミスタに加えられた温度急変状態の温度差の63.2%の変化をサーミスタがするのに要する時間であると定義できる。
図からもわかるように，変化は始めが大きく，次第にゆるやかに変化しながら最終値に近づいてゆく。

サーミスタの応答は，測定場所の媒体の種類や状態で変化するものであり，測定媒体の状態を定めて規定する必要がある。一般的には媒体の比熱や熱伝導率，粘性に関係し気体より液体，液体より金属に対して，また静止しているものよりも流れているものに対して応答が速く（時定数が短く）なる。

 

サーミスタの電流―電圧（I-Ｖ）特性

グラフ上での座標軸の関係から見ると電流一電圧特性と呼ぶべきなのかも知れないが，電圧一電流（V-I)特性と呼ばれることが多い。熱放散定数で述べたように，抵抗体であるサーミスタに流れる電流をゆっくりと次第に増やしてゆくと，ジュール熱を発生しその量もだんだん増えてゆく。発熱量が少ない間は発生した熱はリード線を伝わるなどしてサーミスタ自体の温度が上昇することはほとんどないが，電流がある程度大きくなると発熱量が放熱量を上回るようになり，サーミスタの温度が少しずつ周囲温度より高くなってくる。

その結果サーミスタの抵抗が低くなる傾向を生じ，電流が小さい間はサーミスタの抵抗が一定で電圧と電流の間にはオームの法則が成立して，（サーミスタの端子電圧は電流と比例し）グラフは直線的に変化していたものが，わずかずつ端子電圧が低下し，グラフが上に凸な曲がりをもつようになる。

さらに電流を増やしてゆくと，サーミスタはますます温度が上がって抵抗が低くなりその端子電圧には極大値を生じ，電流を増すと電圧が低下するようになる。このようにサーミスタに流れる電流が増えたときその端子電圧が低下する領域をサーミスタの負性抵抗領域と呼んでいる。

サーミスタの熱放散定数が大きいほど，サーミスタの抵抗が影響を受け始める電流が大きくなるので, PSB-S1のサーミスタのI-V特性のカーブを見るとカーブの極大値を生ずる電流が少しずつ変化し，電圧の極大値が熱放散定数δが大きいサ－ミスタほど高い値をとっていることがわかる。

下図はPSB-S1のI-Ｖ特性のカーブである。熱放散定数δは1.3 mW/℃である。

 

 

 

 

 

 

 

 

 

 

 

 

サーミスタの最適な回路定数

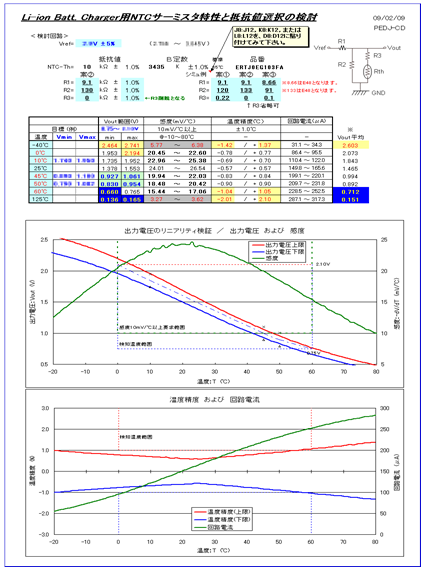
サーミスタの最適な回路定数はPanasonicサイトにて

①基本回路構成②基準電圧③制御温度範囲と出力電圧範囲④目標制御温度と目標出力電圧を指定すれば

下記の主要特性値の計算表＆グラフを作成してくれて

①出力電圧（上下限）②感度（mV/℃）③温度精度　④回路電流

且つ、回路定数を変化させてシミュレートし、最適な回路定数をご提案しても貰えます。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

サーミスタを選ぶ時の注意事項

どのような観点に立って，使用温度範囲で適当な抵抗値のサーミスタを選定すればよいかについて述べる。

消費電力，自己加熱の観点から

熱放散がある値のものとしたとき，自己加熱による誤差を前もって認識するためには，消費電力と熱放散定数についてよく知っておかなければならない。使用するサーミスタの形状・構造が決まったら，最初に熱放散定数を調査する。　δの概略の値がわかったら使用目的から許される温度誤差の何分の１かの自己加熱に抑えられるような消費電力を考え，そのときのサーミスタの抵抗値と回路からサーミスタに流れる電流を想定してみる。

抵抗を低く選べば電流を多く流すことができるがW=i²×Rの関係があるので，一般的には抵抗を高くした方が電流が減り，消費電力を低く抑えやすい。

しかし体温計の場合などには，電池の交換がしにくいので，電池の寿命を長くするという単純な立場から非常に高い抵抗値のサーミスタを選定する場合が多い。

 

絶縁抵抗の観点から

この立場から見ると抵抗が余り高くない方がよい。サーミスタは白金測温体などと比較すると抵抗が高いので，わずかな絶線不良があってもサーミスタと並列に入ったようになっている抵抗の影響を大きく受ける心配がある。

 

誘導障害という観点から

最近のように多種多様な電子機器が使われ，その周波数も広い範囲にわたっていることを考えると，抵抗が低い方が誘起電圧が低くなるので受ける影響が小さくなる。

誘導障害を受ける心配があるときにはシールド線を使い，センサ部分には金属製保護管を使用し接地するように心掛げる。　２本の心線を互いに強く撚り合わせた状態の電線を使うことも大切な点である。大電流が流れている電線が近くに平行におかれているようなときには，必ず電線管にセンサケーブルを通し，お互いにできるだけ距離を離して配置する。

磁力線に対する対策としては鉄板による遮断が有効である。強い電磁界内ではセンサやケーブルが振動するような取り付け状態は，誘導を受げやすくするので注意する必要がある。

マッチングという観点から

サーミスタに接続される回路との抵抗のマッチングを考慮に入れる。回路側の入力インピーダンスは高い方がよい。そのためにサーミスタ回路の抵抗が高すぎると問題を生じやすい。精度が高い結果を求められている場合には特に注意する。