確率 probability 【イラスト図解】
英語:probability 中国語:概率
確率とは
ある事象の起こりやすさの尺度。
ある試行を同じ条件の下で長く続けたとき,一定の結果が生起する相対頻度の極限値より一般的にはランダムな事象に割り当てられている[0,1]の範囲の実数値と定義される。
一般に事象Aの確率を Pr(A)で表す。
参考:ある事象が生じるという信念の度合いを表す主観確率という概念も存在する」
(Z 8101-1)
ある確率現象が起こる確からしさを表す,何らかの意味で合理的な尺度。
現代数学においては,測度論と呼ばれる理論体系の中で抽象的に定義される。
普通使われる古典的な定義では,同様に確からしいnとおりのうちのnとおりが事象Aに対応するとき,Pr(A)=m/nをAの生起する確率とする。
これは,仮想的な多数回の試行中でのAの出現率(相対度数)の極限と考えることができる。
解析者の思いこみの強さ(信念)を確率とみなし,整合性のある体系を公理論的に構成する主観確率の立場もあり,意思決定理論の基礎として採用されることもある。
事象A、Bが排反事象ならば,このうち少なくも一つが起こる確率はPr(A∪B)=
Pr(A)十Pr(B)となる(加法定理)。
また,A,Bが同時に起こる確率は,Bの条件付き確率Pr(B|A)によりPr(A∩B)=PrA)Pr(B|A)で表される(乗法定理)。
引用先:クォリティーマネジメント用語辞典 日本規格協会
確率の求め方
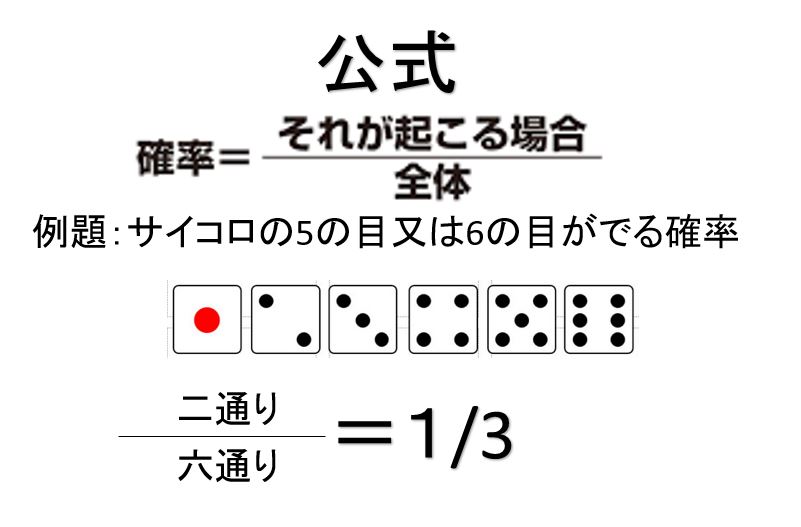
公式は確率=(それが起こる場合)/(全体)
例として、サイコロを投げて3の目が出た場合、1~6の目があるから、 全体は6通り 。 4の目が出るのは1通りだから、は1、よって確率は1/6。
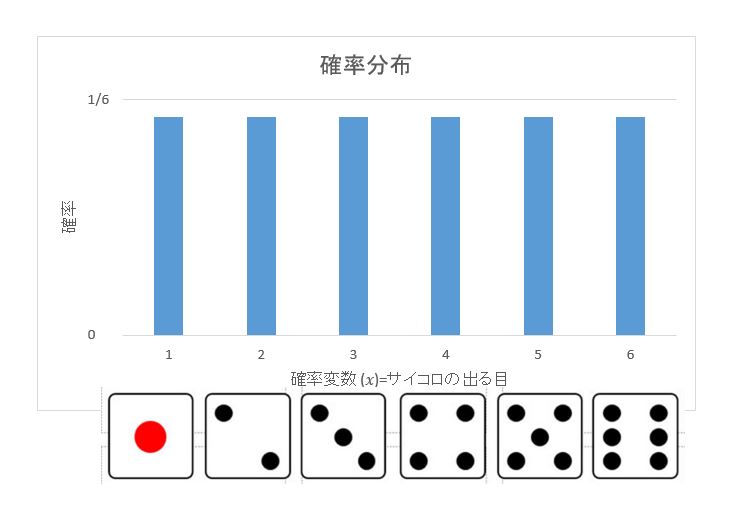
確率分布とは
確率分布とは、確率変数がとる値ごとの確率の分布、確率変数ごとの確率の合計は、1となります。例えば、サイコロを振ったとき、1から6のどの目が出るかの確率分布は、以下の図のようになり、1からの6の目の確率の合計は1となります。
確率計算サイト
以下のサイトで確率の計算がネット上で計算可能です。
計算サイト
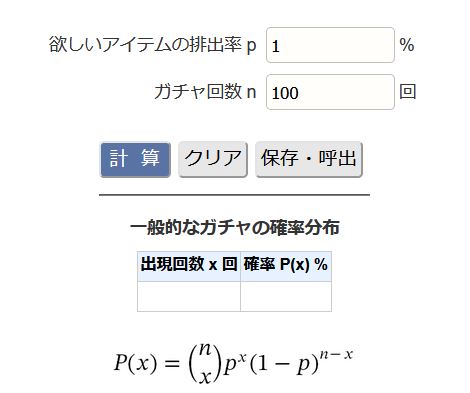
ガチャの確率分布の計算
スマホゲームなどの一般的なガチャにおいて、ガチャを何回か回したときに欲しいアイテムが出現する回数の確率分布を計算します。