はじめての「回帰分析」を、統計が苦手な人でもスラスラ読めるように、基礎から実務レベルの使い方まで一気に解説します。
Excel/Googleスプレッドシートで“いますぐ”試せる手順も用意しました。最後まで読めば、明日から自分のデータで回帰分析が回せるようになります。
回帰分析とは?基礎知識の解説
回帰分析の目的と重要性
回帰分析は「数値を予測」し、「要因がどれだけ効いているか」を把握するための統計手法です。
例:広告費から売上を予測/面積や駅距離から不動産価格を予測/CV(コンバージョン)する確率を推定、など。
主な目的は下記です。
① 予測(Prediction)
たとえば、過去の販売データから「広告費」をもとに「売上」を予測したい場合、
回帰式を使えば次のように予測できます:
このように、説明変数(広告費)から目的変数(売上)を予測できるのが回帰分析の最大の目的です。
-
目的変数(従属変数):予測したい数値(売上、価格、CV確率 など)
-
説明変数(独立変数):影響する要因(広告費、面積、駅距離、季節 など)
-
モデル:説明変数を合体させ、目的変数を近似・予測する式のこと
② 関係性の把握(Relationship Analysis)
どの変数が目的変数に影響しているか、またその「影響の強さ」や「方向(正 or 負)」を明らかにします。
たとえば:
-
温度が上がるとアイスの売上が増える → 正の相関
-
値上げすると売上が減る → 負の相関
③ 要因分析・改善への応用
製造現場では、品質(例:寸法、重量)に影響する要因(温度、圧力、作業者など)を数値的に評価して、
どの要因を改善すれば品質が安定するかを見える化できます。

回帰とは何か?基本的な概念
「回帰」とは、あるデータ(結果)を、その原因や要因に“戻して(回帰して)”説明すること
を意味します。
「回帰(regression)」という言葉は、19世紀に統計学者**フランシス・ゴルトン(Francis Galton)**が使ったのが始まりです。
彼は「親の身長が高くても、子どもの身長は平均に“戻る傾向”がある」ことを発見しました。
この“平均への回帰(regression toward the mean)”という現象から、
“regression”=「平均に戻る」「傾向を説明する」
という意味が広がったんです。
たとえば、
例)アイスの溶ける速度(Y)と気温(X)の関係を調べる
-
気温が上がるほど溶ける速度が速くなる
-
その関係を表す線が「回帰直線」
つまり、「YがどのようにXに回帰(関係づけられる)しているか」を分析するのが回帰分析です。
線形回帰モデルでは、
y=α+βx+ε
α:切片(X=0のときのYの値)
β:回帰係数(Xが1増えるとYがどれだけ変わるか)
ε:誤差(説明できない部分)
この式をもとに、最もよくデータに合うようにαとβを推測します。
回帰直線の発見
回帰直線を始めて示したのは,イギリスの統計学者のゴルトン(Sir Francis Galton, 1822-1911)である。ゴルトンは多数の「親子の身長」を調べた結果、
[背の高い親の子も背が高い傾向にはあるが親ほどでない],また「背の低い親の子も背が低い傾向にはあるが親ほどでない」という現象を見出した。つまり,子は全体に親より平凡な方向,平均値に近づくいう法則を示した。これを平均への回帰と呼ぶ。
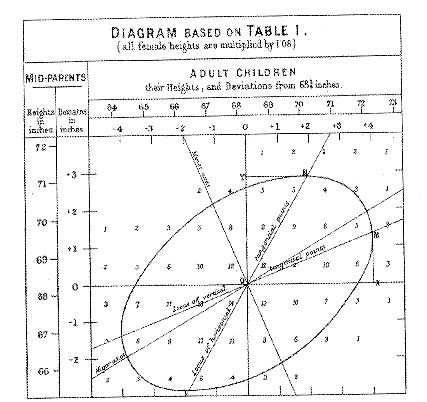
さらに,ゴルトンは,縦軸に「親の身長」と横軸に「子の身長」を示し,それを楕円で囲むことを考えた(下図)。
図の中に,横軸と平行かつ楕円の接線である水平線YNがある。さらに,直線ONが見られる。直線ONが親の身長から子の身長を予測する回帰直線である。点Nの座標を(x,y)とすると,親は背の高さyは約71インチである。しかし,その子の背の高さの予測値xより小さく,約70.2インチである。つまり,子は親より背が高くないことがわかる。
また,同様に,直線OMは子の身長から親の身長を予測する回帰直線である。図の中には楕円の長軸も示されているが,回帰直線OMの傾きは長軸の傾きより小さい。このように,ゴルトンはこの図を使って,平均への回帰の現象をより正確に解釈した。
ちなみにゴルトンは,看護師でもあり統計学者でもあるナイチンゲール[Florence Nghtingale, 1820-1910)のいとこの夫でもあったのでナイチンゲールの意思を汲み,ゴルトンはロンドン大学に統計講座設立の準備をする。
1911年,二人の死後,最初の教授として友人の統計学者ピアソン(Karl Pearson1857-1936)が着任する。これが世界ではじめての統計講座となる。次の教授がフィッシャー(Sir Ronald Aylmer Fisher, 1890-1962)で推測統計の基盤が出来上がる。
回帰分析とは?
相関係数は2つの変数xとyの間の直線的な関係の強さを測る尺度であり,-1から1の値をとる。この2変数間に因果関係を前提とすることはなく,xとyを逆にしても相関係数は同じである。
たとえば,テストAの成績をxとし,テストBの成績をyとして相関係数を求めても,テストAの成績をyとし,テストBの成績をxとして相関係数を求めても同じ値になる。
一方,2つの変数xとyの間に何らかの因果関係を想定し,変数xから変数yの値を予測することを回帰分析という。この意味から,変数xを説明変数,変数yを被説明変数,目的変数などと呼ぶ。
また,直線の式y=α+βyより予測するとき,この直線を回帰直線,α(アルファ)とβ(ベーダ)を回帰係数という。次の例を用いて,これらの内容をさらに説明する。
回帰直線
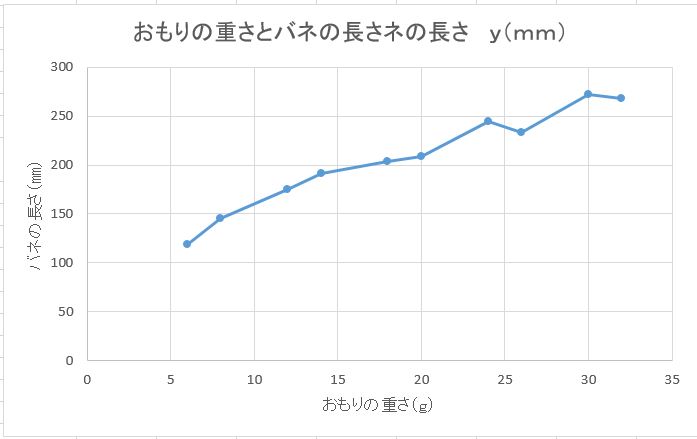
あるバネに10種類のおもりをつるして,バネの長さを測定したところ,下表のような結果が得られた。この結果からx(g)のおもりに対するバネの長さy(mm)を予測したい。
表 おもりの重さとバネの長さ
| 回数 | おもりの重さ x(g) |
バネの長さ y(mm) |
| 1 | 6 | 119 |
| 2 | 8 | 145 |
| 3 | 12 | 175 |
| 4 | 14 | 191 |
| 5 | 18 | 204 |
| 6 | 20 | 209 |
| 7 | 24 | 244 |
| 8 | 26 | 233 |
| 9 | 30 | 272 |
| 10 | 32 | 268 |
図は,このデータの散布図である。この図から,おもりの重さxとバネの長さyの関係として,直線の式
y=α十βx
があてはまるのではないかと考えられる。ここで,αは切片でβは直線の傾きである。この直線が適切であれば,おもりの重さに対するバネの長さが予測できる。
さらに,データから回帰係数 \( \alpha \) と \( \beta \) の推定値 \( \hat{\alpha} \) と \( \hat{\beta} \) が求まったなら,予測値 \( \hat{y} \) も求めることができる。
たとえば,このバネに 10g のおもりをつるしたときのバネの長さは,直線の式 \( \hat{y} = \hat{\alpha} + \hat{\beta}x \) に \( x = 10\,(\mathrm{g}) \) を代入すれば予測値 \( \hat{y}\,(\mathrm{mm}) \) が計算できる。また,バネの自然長は \( x = 0 \) を代入すればよく,そのときの値は \( \hat{\alpha}\,(\mathrm{mm}) \) となる。
統計学では,上記のように,推定値や予測値を表す記号として,^(ハット)を用いることが多い。
最小二乗法(Least Squares Method)
回帰直線の回帰係数aとβを推定する方法の1つに最小二乗法がある。ここでは,最小二乗法を用いて回帰係数の推定値a,βの求め方を説明する。
最小二乗法とは、
「データのばらつきをできるだけ小さくするように、直線(または曲線)を求める方法」です。
もう少し専門的に言うと観測値yiとモデルによる予測値y ^iの**誤差の二乗の和(残差平方和)**が最小になるように、パラメータ(回帰係数)を求める方法です。
🔹 モデルの基本形
単回帰モデル(1つの説明変数)では:
yi=α+βxi+εi
ここで
yi:観測された目的変数(たとえば製品重量など)
:説明変数(たとえば温度など)
α:切片(回帰直線がy軸と交わる点)
β:傾き(xが1増えるときのyの増加量)
εi:誤差(残差、モデルと実際のズレ)
🔹 残差平方和を最小にする
各データ点の「誤差(残差)」は:
$$
e_i = y_i – \hat{y}_i
$$
これを二乗してすべて足した値を「残差平方和」といいます:
$$
SSR = \sum_{i=1}^{n} (y_i – \hat{\alpha} – \hat{\beta}x_i)^2
$$
このSSRが最も小さくなうようにαとβを求めるのが最小二乗法です。
🔹 微分して最小値を求める
最小値を求めるためにαとβで偏微分して 0 とおきます。
\[
SSR(\alpha,\beta)=\sum_{i=1}^{n}\bigl(y_i-\alpha-\beta x_i\bigr)^2
\]
\[
\frac{\partial SSR}{\partial \alpha}
=-2\sum_{i=1}^{n}\bigl(y_i-\alpha-\beta x_i\bigr)=0,\qquad
\frac{\partial SSR}{\partial \beta}
=-2\sum_{i=1}^{n}x_i\bigl(y_i-\alpha-\beta x_i\bigr)=0
\]
\[
\begin{cases}
\sum_{i=1}^{n}(y_i-\alpha-\beta x_i)=0\\[4pt]
\sum_{i=1}^{n}x_i(y_i-\alpha-\beta x_i)=0
\end{cases}
\;\Longleftrightarrow\;
\begin{cases}
n\alpha+\beta \sum x_i=\sum y_i\\[4pt]
\alpha\sum x_i+\beta \sum x_i^2=\sum x_i y_i
\end{cases}
\]
これを連立して解くと、次の式が得られます:
\[
\bar x=\frac{1}{n}\sum_{i=1}^{n}x_i,\qquad
\bar y=\frac{1}{n}\sum_{i=1}^{n}y_i,\qquad
S_{xx}=\sum_{i=1}^{n}(x_i-\bar x)^2,\qquad
S_{xy}=\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)
\]
\[
\hat\beta=\frac{S_{xy}}{S_{xx}},\qquad
\hat\alpha=\bar y-\hat\beta\,\bar x
\]
ここで,\(\bar x\)とSxは変数xの平均値および標準偏差,\(\bar y\)と変数Syは変数yの平均値および標準偏差,Sxyとrxyはxとyの共分散および相関係数である。
この式から,直線の傾きβの推定値\( \hat{\beta} \) は相関係数rxyに標準偏差の比率sy/sxを掛けたものであることがわかる。つまり,回帰直線の傾きと相関係数には関係があることがわかる。
表の『おもりの重さとバネの長さ』のデーターについてこれらを求めると
$$ \hat{\beta}=401/73=5.5 $$
$$ \hat{\alpha}=206-5.5×19=101.5 $$
となる、これから回帰直線はy=101.5+5.5xとなり、おもりの重さに対するバネの長さが予測できる。
たとえば,おもりの重さが20gの場合,バネの長さはy=101.5+5.5×20=211.5(mm)
ここで注意したいことはおもりの重さが20gの場合、バネの長さが丁度、221.5㎜になるのではない。この値は予測値であって平均的に221.5㎜になると推測する。
回答:得られた回帰直線より直線の式 \( \hat{y} = 101.5 + 5.5×30=266.5(㎜) \)と予測される、又、残差は272-266.5=5.5(㎜)である。
回帰分析の種類と選び方
単回帰分析の特徴と利用シーン
-
特徴:目的変数が連続値、関係が直線(線形)に近いときに有効
-
利用例:広告費→売上、面積→価格、温度→歩留まり
-
利点:解釈がシンプル、実装が容易、計算負荷が低い
単回帰分析:1つの説明変数が1つの目的変数を導くとき、それを分析することを単回帰分析という。 例として子供の自転車の上達度という結果(目的変数)は、練習した時間に大きな影響を受けるので、要素(説明変数)が1つしかないと想定して単回帰分析で分析する。
単回帰分析で予測
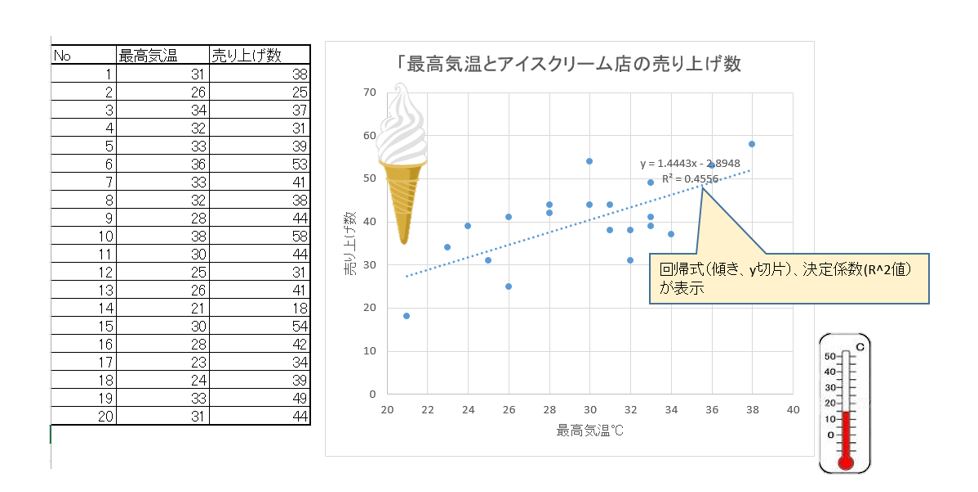
コンビニ店ののアイスアイスクリームの売り上げ数と最高気温から今日の来店客数から予測する場合。
回帰式から今日の最高温度が分かれば客数が予測できる!
重回帰分析とは?その効果とメリット
-
特徴:説明変数が複数。交絡を抑えて純粋な影響度を推定しやすい
-
利用例:売上 ~ 広告費 + 価格 + 競合数 + 季節ダミー
-
メリット:多面的なコントロール、より高精度な予測
重回帰分析:二つ以上の量的な説明変数から、一つの目的変数を予測する手法。 たとえば、接客の質や品数、売場面積などを変数とした小売店の売上などを予測するといった分析です。
重回帰分析で予測
日本経済の消費関数の予測をする。
被説明変数は消費(c)、説明変数は、所得(y)と利子率(r)である。
エクセル等で偏回帰係数で求め、説明変数が確定したら実際に必要な数値を重回帰式に代入し、目的変数(結果)を算出します。
重回帰式:
目的変数=(偏回帰係数×説明変数1)+(偏回帰係数×説明変数2)+(偏回帰係数×説明変数3)+…+定数項
上記の例の場合は推定された回帰式は, 次のようになる。
消費(円)= 0.402×所得(円)- 3032.417×利子(%)+78203.078
ロジスティック回帰の基本と応用
-
特徴:目的変数が**2値(Yes/No、CV/非CV)**のときに使う
-
出力:その事象が起こる確率(0〜1)
-
応用:離反確率予測、CV確率、審査合否、メール開封確率 など
ロジスティック回帰分析:目的変数が0と1からなる2値のデータ、あるいは0から1までの値からなる確率などのデータについて、説明変数を使った式で表す方法、ある事象が起こる確率を予測することができます。
ロジスティック回帰分析で予測
ロジスティック回帰分析は2値に分類する手法です。
ロジスティック回帰分析を行うことで、商品が売れるかどうか、サービスを継続してくれるかどうかなど「はい」か「いいえ」で知りたい情報を予測できます。
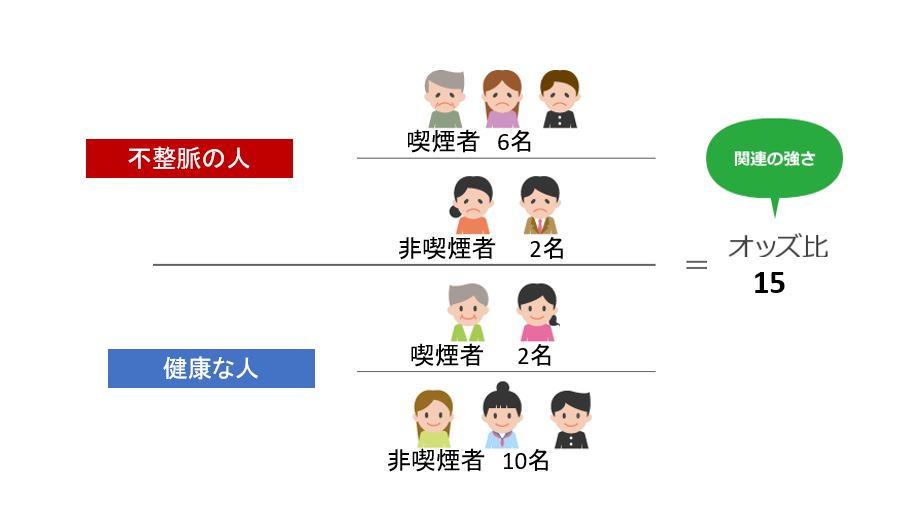
例えば不整脈症状が「ある患者」と「ない患者」のグループに喫煙有無、飲酒有無、ギャンブル嗜好についてのアンケートに回答してもらい、喫煙、飲酒、ギャンブルによる不整脈症と関係を調査します。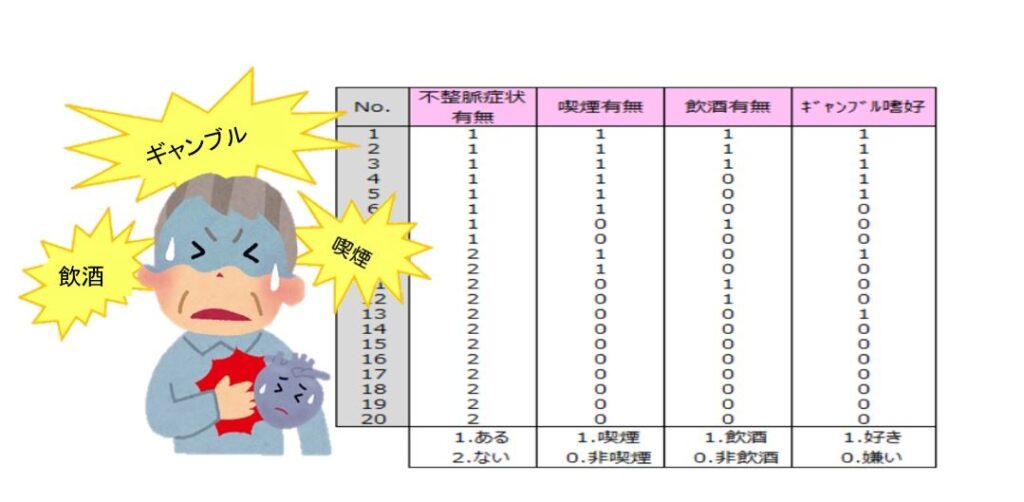
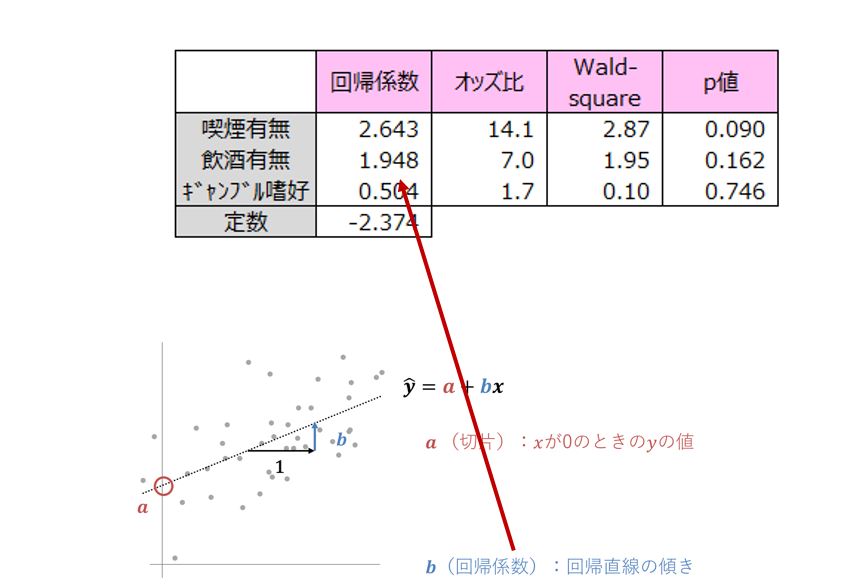
エクセル、SPSS等の統計分析ソフトを使用して回帰係数、オッズ比を算出します。
回帰係数はモデル式の係数です。
オッズ比は説明変数の目的変数への影響度を調べる尺度です。値が大きいほど影響度が高い項目といえます。オッズ比から、不整脈症状の原因要因の1位は喫煙の有無で、次に飲酒の有無となります。ギャンブル嗜好は、不整脈症状にそれほど影響がないことがわかります。
*オッズ比とは
ある因子(環境・食べ物・嗜好品等)がある病気の原因であると仮定したとき、その因子と病気との間に関連があるか無いかを調べます。
オッズ比とは、その関連の強さの指標で、オッズ比が高いほど、その因子と病気の関連性が高いことを示します。
各種回帰分析の目的、違いと選択基準
-
目的変数が連続→線形/重回帰
-
目的変数が2値→ロジスティック回帰
-
明らかな曲線関係→多項式回帰や非線形回帰も検討
-
特徴量が多い/相関が強い→正則化(リッジ、ラッソ)で汎化性能UP
| 回帰の種類 | 主な目的 | 例 |
|---|---|---|
| 単回帰分析 | 1つの要因と結果の関係を見る | 温度と製品重量の関係 |
| 重回帰分析 | 複数の要因を同時に考慮 | 温度・圧力・時間が重量に与える影響 |
| ロジスティック回帰 | 結果が「合格/不合格」など2値のとき | 検査合格率を要因から予測 |
| 非線形回帰 | 曲線的な関係を表現 | 成長曲線や経時変化のモデル化 |
重回帰分析と単回帰分析との違い
単回帰分析とは、ひとつの要因から結果を分析・予測する統計的手法です。例えば、広告費と売上の相関関係を求める際に用いる。「広告費を○○円にしたら売上が△△円になった」というような実績データを集め、回帰係数を探す。そしてグラフにして「y=ax+b」といった回帰式を求める。
「y」は目的変数、「x」は説明変数、「a」を回帰係数という。広告費が説明変数、売上が目的変数とするなら、この式のxにいくつか数字を当てはめることで、広告費に対する売上がわかる。
一方、重回帰分析は、複数の説明変数を含む回帰分析です、以下は、広告費・店舗面積・スタッフ数という複数の説明変数と売上という目的変数から成る重回帰分析の例です。
単回帰分析と重回帰分析では、検証する内容や結果が異なるため、どちらの手法を使って回帰分析をするのかが重要となる。
ただし実際のビジネスでは、売上を決める要素はひとつではない。飲食店なら立地や駅からの距離、価格帯、天気などの要素が売上に影響する。結果と複数の要因の因果関係がわかれば将来を予測可能です。
そのため、ビジネスの場面では、2つ以上の要素を用いる重回帰分析のほうが、予測精度を高めるのに適切です。
基本的な構造は変わらないが、重回帰分析は単回帰分析より説明変数が増えるので、式がその分長くなる。
重回帰分析の式は「y=a_1 x_1+a_2 x_2+a_3 x_3+a_4 x_4…a_p x_p+b_0」
分析の流れは、単回帰分析も重回帰分析もほぼ同じです。
重回帰分析をするためには、上記の式で計算したり専用のソフトやExcelを使ったりして求める必要がある。またある程度の理解度がないと結果の解釈やそこから導く予想ができないケースもあるため、注意が必要です。
重回帰分析の利点
重回帰分析の利点としては、主に以下の2点が挙げられる。
現実に即した分析可能
重回帰分析は、複数の変数を同時に考慮できるため、現実の複雑な状況をより正確に反映した分析が可能です。
例えば不動産の価格を予測する際に面積だけでなく立地や築年数、周辺の設備など複数の要因を同時に考慮することで、より現実に即した価格予測が行え、単一の要因だけでは見落としがちな相関関係や影響度を把握できる。
費用対効果の高いマーケティング
重回帰分析を用いることで、マーケティング活動の各要素が売上にどの程度影響しているかを定量的に評価できるようになる。これにより、どのマーケティング活動が最も効果的かを判断し限られた予算をより効果的に配分することが可能となります。
例えばオンライン広告の投資が売上増加に最も寄与していることが分析から明らかになれば、その領域への予算配分を増やすことで、全体のマーケティング効果を最大化できる。
重回帰分析の具体例
・マンション経営
マンション経営では、家賃収入が売上となるため「家賃をいくらにすればよいか」が重要。なぜなら家賃の金額が適正でないと空室リスクを負うからである。
家賃の金額が決まる要因は、駅に近いかどうかや部屋の広さ、設備の充実度合い、築年数などさまざまだ。重回帰分析では、駅に近いかどうかや部屋の広さや設備、築年数などの要因が「説明変数」、家賃の金額が「目的変数」となる。
・飲食店経営
飲食店は、売上高の大小により店舗の経営状態が大きく変わってくるのが特徴です、そのため飲食店の経営をするうえで重要なのが「売上がいくらになるのか」を予測することである。
飲食店では、さまざまな要因が売上の結果に影響を与える。具体的な要因としては、店舗の面積やスタッフ数、メニュー内容、駅からの距離、駐車場の有無などが挙げられる。
重回帰分析では、店舗の面積やスタッフ数、メニュー内容、駅からの距離、駐車場の有無などの要因が「説明変数」、売上高が「目的変数」となる。重回帰分析を活用すれば、新規店の各要因から将来の売上の予測が可能です。
具体的な回帰分析のやり方:ステップバイステップ
データの収集と準備方法
-
目的の明確化:何を予測・説明したい?(例:来月の売上)
-
データ収集:売上、広告費、価格、競合指標、季節などを期間一致で集める
-
前処理:欠損補完、異常値確認、単位統一、カテゴリはダミー変数化
-
分割:学習データ/テストデータを分ける(例:80/20)
エクセルを使った基本的な回帰分析の手法
**単回帰(売上 ~ 広告費)**の例
-
データを2列(広告費、売上)で用意
-
データ分析アドイン →「回帰」
-
目的範囲=売上列、説明範囲=広告費列
-
出力で係数(傾き・切片)、決定係数(R²)、p値を確認
-
散布図+近似直線(グラフ要素)で視覚化
重回帰は説明範囲に複数列を指定するだけ。
カテゴリ変数は0/1のダミー列を作成して追加します。
Googleスプレッドシートでの回帰分析の実施
-
単回帰の係数は
SLOPE(売上範囲, 広告費範囲)、切片はINTERCEPT(...) -
相関は
CORREL(売上範囲, 広告費範囲) -
より本格的には
LINEST関数(多変量対応)で係数・統計量を取得 -
散布図→「傾向線」→「多項式」等で関係の形を素早く確認
スプレッドシートは関数の再計算が速いので、仮説検証の初期探索に向いています。モデル確定後はPythonで再現可能なスクリプト化が便利。
回帰分析の結果の見方と解釈
モデルの評価指標:決定係数とは?
-
決定係数(R²):モデルが目的変数の変動をどれだけ説明できたか(0〜1)
-
調整済みR²:説明変数が増えても過大評価しにくい指標
-
RMSE/MAE:予測誤差の大きさ(小さいほど良い)
R²が高い=良いモデル、ではありません。外部データ(テスト)での汎化性能を必ず確認。
相関係数の意味と重要性
-
**相関係数(Pearson’s r)**は線形の結びつきの強さ(-1〜+1)
-
相関が高くても因果とは限らない/多重共線性の兆候にも注意
外れ値の影響とその対策
-
影響:係数が引っ張られ、誤った解釈・予測に
-
対策:箱ひげ図・標準化残差で検出、ロバスト回帰や変数変換(対数化)、外れ値の業務的妥当性を確認して除外基準を明文化
回帰分析の活用事例
ビジネスにおける売上予測の例
-
目的:翌月売上
-
説明:広告費、価格、販促回数、季節ダミー、在庫指標
-
成果:在庫切れ率の低下、広告費配分の最適化
マーケティング施策における回帰分析の役割
-
ロジスティック回帰でCV確率をスコア化→高確率セグメントに重点投下
-
価格×キャンペーン×チャネルの交互作用を重回帰で把握→施策ミックスの改善
不動産市場における価格予測の実例
-
面積、築年数、駅距離、階数、方角、行政区ダミー
-
係数から「1m²あたりの寄与」「駅距離のペナルティ」を定量化 → 査定根拠の透明化
回帰分析を行う際の注意点
・2変数間の関係が直線的と見なせない場合,回帰直線ではなく2次曲線などの方が当ではまりがよいことがある。
・外れ値がある場合,その値に影響されるので,求められた式を解釈するときには注意がいる。
・複数のグループが混在している場合,グループごとに回帰直線を求める方が好ましい。
上記以外に,回帰分析の予測に関する注意点が2つある。
・一般に,求められた回帰直線を用いて被説明変数yから説明変数xを予測してはいけない。これは,yの残差に対する最小二乗法を用いて回帰直線が導出されるためである。
・与えられたデータが存在する範囲から大きく離れている値xに対しては,直線的な関係が成立しない可能性があるので,単純に予測に利用してはいけない。離れた値を回帰分析のxに代入し予測値を求めることを『外挿』といい,外挿は避けるべきとされている。
たとえば,「おもりの重さとバネの長さ」のデータでは,おもりの重さが35g程度までのバネの長さが測られているが,おもりの重さ100gではこの関係が利用できかどうかは保証されず,バネの長さは予測すべきではない。
多重共線性の問題とその解決策
-
症状:説明変数同士の強い相関→係数が不安定、p値が跳ねる
-
検知:VIF(分散拡大係数)。一般に10超は要注意
-
対策:相関の高い変数を絞る、主成分で圧縮、リッジ/ラッソの正則化
データの質が結果に与える影響
-
測定誤差・欠損・期間ズレはモデル精度を直撃
-
粒度(日次/週次)、定義の一貫性、外部要因(祝日・天候)を明記
-
再現性のために前処理と特徴量作成の手順をスクリプト化
おすすめの書籍と参考文献
よくある質問(FAQ)
Q1. R²が低いです。モデルは失敗?
A. いいえ。現実のデータはノイズが多く、R²が0.3〜0.6でも意思決定に使える場合があります。RMSE/MAE、残差の偏り、代替特徴量の追加や期間見直しも検討しましょう。
Q2. 説明変数が多すぎます。どう選べば?
A. まずは相関行列とVIFで絞り、次にラッソで自動選択。業務知見で意味のある変数を残し、同義のものは統合を。
Q3. ロジスティック回帰の出力(確率)のしきい値は?
A. 既定の0.5に固執せず、ビジネスの損益で最適化を。ROC曲線やF1、事業KPIに合わせたカスタムしきい値が有効です。
おすすめ 関連記事
下記の記事も参照 願いします。
























コメント