エクセル ヒストグラム(度数分布図)作り方
エクセルによるヒストグラム(度数分布図)の書き方、作り方およびテンプレートについて図解入れで解説しています。
おもな内容は下記のとおりです。
・ヒストグラム(度数分布図) データー区間 決め方
・ヒストグラム(度数分布図) 読み取り方
・度数分布図 ヒストグラム 違い
・度数分布図 階級、中央値
・ヒストグラム 作り方、書き方等です。
業務での統計解析での参考になれば幸いです。(*^_^*)
具体的なヒストグラムを用いた分析、改善事例は下記の記事を参照してください。
関連記事:エクセル版 ヒストグラム(度数分布図)による工程解析 改善事例
ヒストグラム(度数分布図)エクセル表 テンプレート
下記にエクセルで作成したヒストグラム(度数分布図)があります、ご自由にダウンロードしてご使用ください。
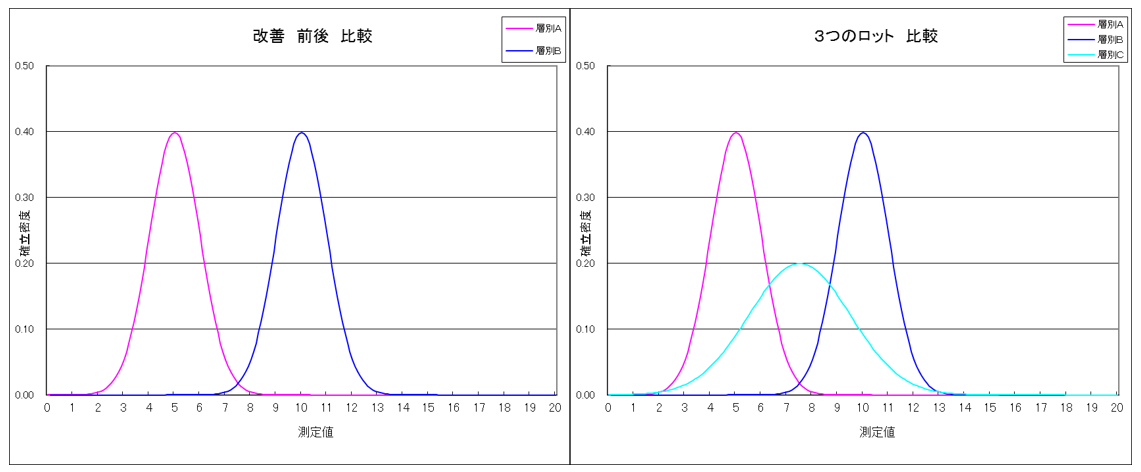
また、平均値および標準偏差だけを入力すれば改善前後のバラツキ度合いが一目でわかる正規分布表(下図)を作成しました、改善後の確認にご活用ください。
ご自由にダウンロードしてご使用ください。
2024年版 わかりやすい ヒストグラム(度数分布表)の作り方~バラツキの見える化~【音声解説付き】
youtube動画でのヒストグラム(度数分布図)作り方の解説です。
3分で分かる! ヒストグラム(度数分布図)の概要
ヒストグラムとは、あるデータの分布状況を視覚的に表すグラフの一種です。特に、量的データ(数値で表せるデータ)の分布を把握する際に用いられます。
ヒストグラムの特徴
横軸: データの値(数値)をいくつかの区間(階級)に分け、その区間を表します。
縦軸: 各区間に含まれるデータの個数(度数)を表します。
棒グラフ: 各区間の度数を高さとした棒グラフで表し、データの分布を視覚的に表現します。
ヒストグラムの役割
データの分布を一目で把握: データがどのあたりに集中しているか、ばらつきがどの程度あるかなどを直感的に理解できます。
異常値の発見: データの中に極端に大きい値や小さい値(異常値)が含まれている場合、ヒストグラムで視覚的に確認できます。
データの傾向の把握: データが左右対称に分布しているか、それとも特定の値に偏っているかなどを確認できます。
ヒストグラムの作り方
データの範囲を決める: データの最小値と最大値から、全体をいくつかの区間(階級)に分けます。
階級幅を決める: 各階級の幅を均等にするのが一般的です。
度数を数える: 各階級に含まれるデータの個数を数えます。
グラフを描く: 横軸に階級、縦軸に度数をとり、各階級の度数を高さとした棒グラフを描きます。
ヒストグラムの活用例
製品の品質管理: 製品の寸法や重量のばらつきを分析し、品質管理に役立てる。
顧客分析: 顧客の年齢や購入金額の分布を分析し、マーケティング戦略に活かす。
実験データの分析: 実験結果の分布を分析し、仮説の検証を行う。
ヒストグラムの種類
度数分布ヒストグラム: 最も一般的なヒストグラムで、各階級の度数を棒グラフで表します。
相対度数分布ヒストグラム: 各階級の度数を全体のデータ数で割った相対度数を表します。
累積度数分布ヒストグラム: ある階級以下のデータの総数を表します。
ヒストグラムの注意点
階級幅: 階級幅の選び方によって、ヒストグラムの見え方が変わります。適切な階級幅を選ぶことが重要です。
データの量: データの量が少ない場合は、ヒストグラムの形が不安定になることがあります。
異常値の影響: 異常値が全体の分布に大きな影響を与えることがあります。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
生成AIでChatGPTでヒストグラムを作成する!【図解】
現在は生成AI ChatGPT及びGemini等が急速に社会に浸透してきており、AIに的確な条件のプロント文を指示せれば正しいヒストグラムが作成される。
『ChatGPTでヒストグラムを作成する!【図解】』については下記の記事を参照 願いします。

ヒストグラム(度数分布図)とは
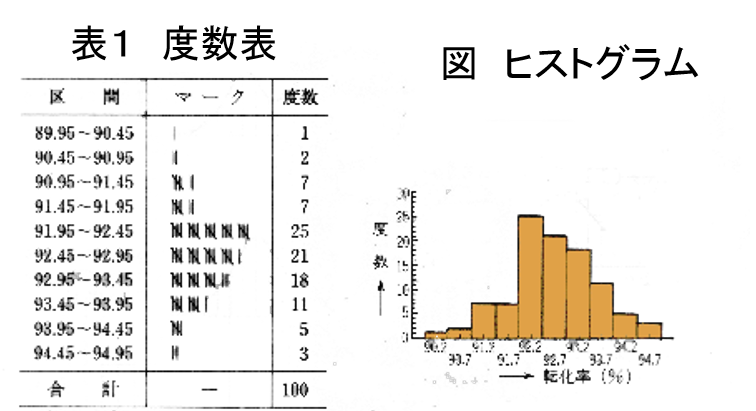
横軸に特性値を,縦軸に度数を目盛って区間の幅で柱状の図を書いた度数図を一般にヒストグラム(histogram)と呼んでいる。
これを規格値と照合したりして,その製品の品質の状態が満足なものであるかどうかを判断するのに役立つ。
表1をヒストグラムに表すと図1のようになる。
度数分布図 ヒストグラム 違い
ヒストグラムは日本語の表記では度数分布図のことであり、柱状図、柱状グラフとも呼んでいる。
ヒストグラム(度数分布図)は英語、中国語(中文)では下記のように表現している。
英語:histogram
中国語(中文):直方图、条形图、矩形图
又、度数分布表は英語、中国語では下記のように表現している。
英語: frequency table
中国語(中文): 频率分布、频数分布
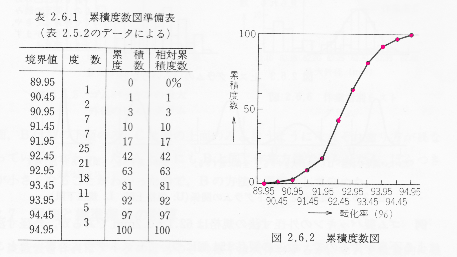
相対累積度数とは|相対累積度数求め方
縦軸に累積度数(cumulativefrequency)または相対累積度数(relative cumulative frequency)を目盛ったグラフ(累積度数図)を書くと,規格値以下のもの,または規格値以上のものが,全体の何パーセントを占めるかを知るのに役立つ。
累積度数とは,ある値以下のデータの個数であり,表1のようにして求めるとわかりやすい。この表から累積度数図を書くと,図1のようになる。
ヒストグラムの役割
同じ工程、同じ作業標準、同じ材料、同じ設備で生産してもでき上がる品物の品質(品質特性)にはばらつきが生じます。品質特性を「測定して得られるデーターの度数はある値を中心に最も多く、中心から離れるに従ってその割合はだんだん少なくなるのが普通です。
これを品物の集団が分布を持っていると言います。
ヒストグラムとはデーターの存在する範囲をいくつかの区間に分けて各区間にはいるデーターの出現数を数えて度数表を作成しこれを図にしたものです。
ヒストグラムの役割は次の通りです。
①分布の状態を見易くし分布の状態を目で見ることができます。
②データーがどんな値を中心にどんなバラツキを持っているかを知ることができる。
③分布がどのような形をしているか知ることができる。
ヒストグラムの作り方 基本
同じ作業者が、同じ材料、同じ設備・機械、同じ作業方法など、同一条件のもとで加工したものでも、そのでき栄えにはバラツキがあります。このバラツキの分布状態を棒グラフで表わしたものがヒストグラムです。
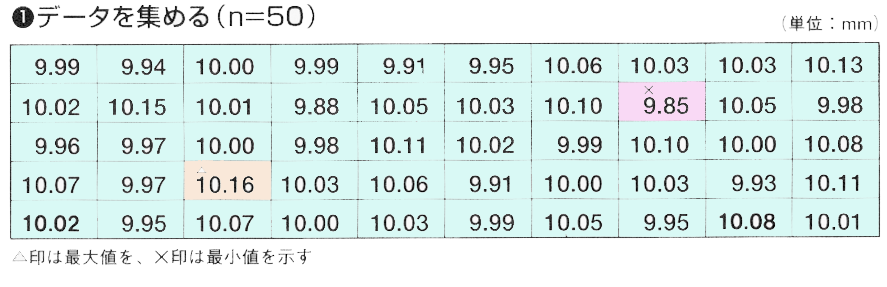
データを集める
データ数は、通常100以上が望ましいといわれています。測定の手間を省くことが必要
な場合などでも、少なくとも50以上集めます。
階級数~スタージェスの公式
階級数を決める場合、スタージェスの公式から求めます。
スタージェスの公式は次のものになります。
数式 n = 1 + log2N
(n:階級数,N:データの総数)
スタージェスの公式 参考表:
| N | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 |
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
上の参考表は「データの全数が大体200個程度なら階級数は8か9くらいにしておけばいい」と目安として使用してください。
階級値、幅の求め方|データの区間幅を算出
データの中から最大値と最小値を探します。この最大値と最小値の差を10で割ります。
なお、区間幅を測定単位の整数としたほうがデータの区分けがしやすいので、測定単位の下位以下を四捨五入します。
区間幅の境界値を決める
最小値側の境界値は、最小値から測定単位の半分を引きます。
最小値側の境界値が決まったら、最小値側の境界値に先に算出した区間幅
を順次加算し、最大値を含む区間幅を算出したところで区間幅の加算をやめ
ます。
相対度数の求め方、算出
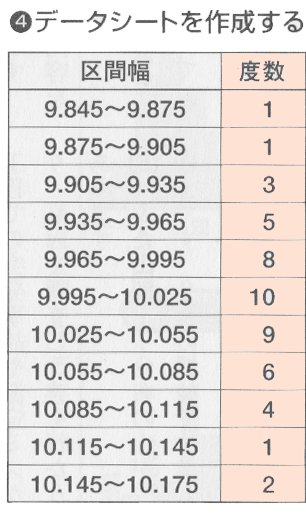
区間ごとのデータ数(度数)を調べるため、データシートを作成します。
それぞれの階級の度数を度数の合計で割ったものをそれぞれの階級の相対度数といいます。
下記の例では,それぞれの度数を,度数の合計100で割っています。
|
10
|
0.10
|
|
|
20
|
0.20
|
|
|
40
|
0.40
|
|
|
20
|
0.20
|
|
|
10
|
0.10
|
|
|
100
|
1 |
相対度数はそれぞれの階級の度数の全体に対する割合です、よってすべてを合計すると1になります。
ヒストグラムを作成する
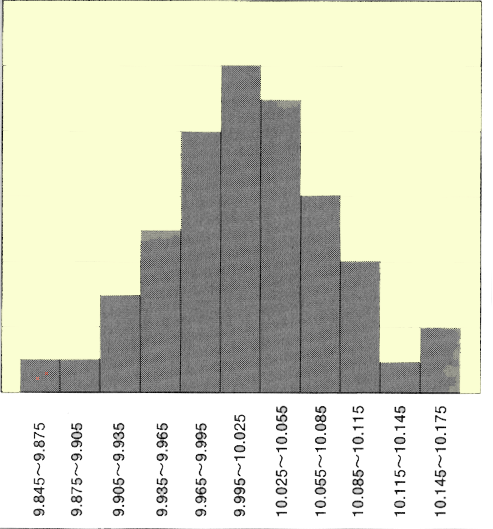
方眼紙を用いて、横軸に測定値を、縦軸にデータ数を取ります。区間ごとのデータ数を棒グラフで表わします。これがヒストグラムです。
ヒストグラムには、表題、集めたデータの記録、作成日、作成者などを記載します。
このようにヒストグラムを作成してみると、データのバラツキの分布状態がひと目わかるようになります。
エクセル2013 ヒストグラフ~分析ツール使用
エクセルの付属しているアドイン 分析ツールを使用すると簡単にヒストグラムが作成されます。その手順を説明します。
Excel エクセル分析ツールのインストール、読み込み
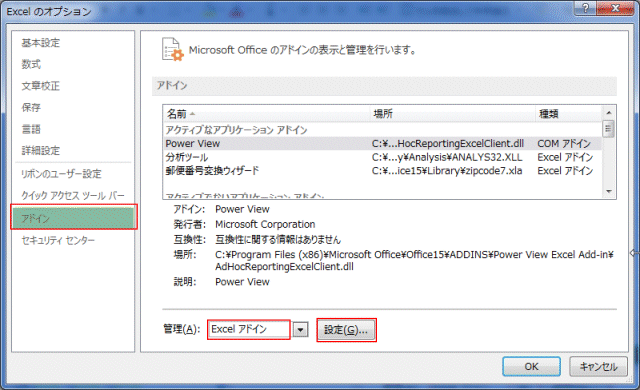
アドインの分析ツールは初期状態では使えませんのでアドイン エクセル分析ツールをインストール、読み込みします。
下記はエクセル2013でのインストールの方法です。
オプション 選択
 この機能を利用するときはアドインで追加します。
この機能を利用するときはアドインで追加します。
[ファイル]タブの[オプション]を実行します。
[設定]ボタン選択
アドイン]を選択し、[管理]ボックスに[Excelアドイン]となっているのを確認して、隣の[設定]ボタンをクリックします。
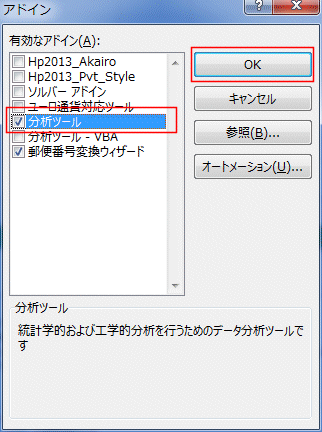
「分析ツール」選択
アドイン ダイアログで「分析ツール」にチェックを入れ[OK]ボタンをクリックします。
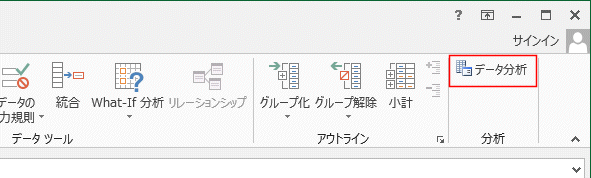
データ分析 表示 確認
[データ]タブの[分析]グループに[データ分析]が表示されていることを確認します。
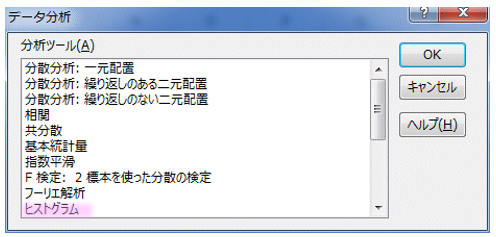
ヒストグラムの選択
[データ分析]をクリックするといろいろな分析ツールが表示されますのでヒストグラムを選択します。
エクセル2010での分析ツールのインストール方法は下記を参照してください。
Excel エクセル2013 分析ツール ヒストグラム作り方
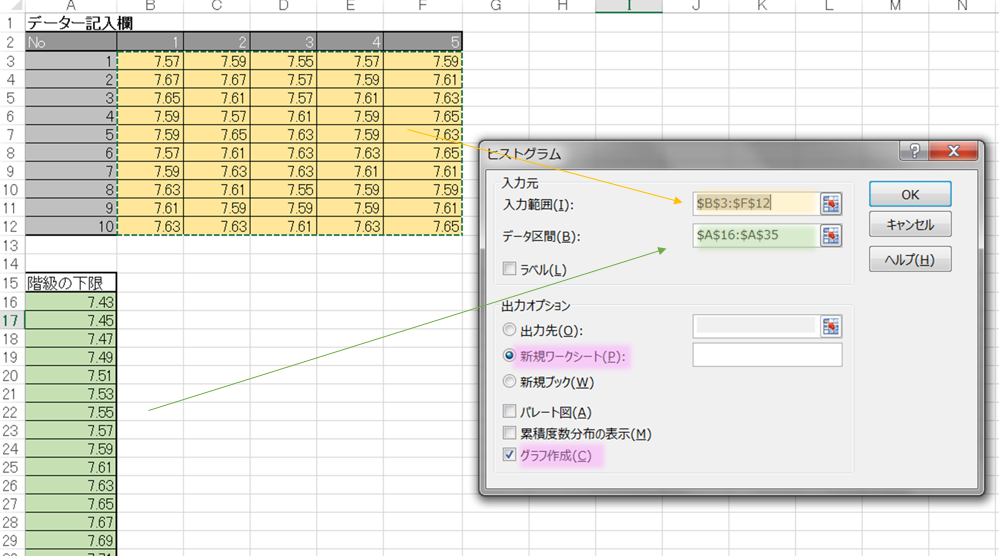
上記のエクセル分析ツールのインストールし、ヒストグラムの選択したら次はいよいよデーターを入力します。
例として下記のデーターを入力します。
データー記入欄
| 7.57 | 7.59 | 7.55 | 7.57 | 7.59 |
| 7.67 | 7.67 | 7.57 | 7.59 | 7.61 |
| 7.65 | 7.61 | 7.57 | 7.61 | 7.63 |
| 7.59 | 7.57 | 7.61 | 7.59 | 7.65 |
| 7.59 | 7.65 | 7.63 | 7.59 | 7.63 |
| 7.57 | 7.61 | 7.63 | 7.63 | 7.65 |
| 7.59 | 7.63 | 7.63 | 7.61 | 7.61 |
| 7.63 | 7.61 | 7.55 | 7.59 | 7.59 |
| 7.61 | 7.59 | 7.59 | 7.59 | 7.61 |
| 7.63 | 7.63 | 7.61 | 7.63 | 7.65 |
入力範囲の設定
1.入力範囲及びデータ区間を設定します。
2.出力オプションで「新規ワークシート」にチェックを入れます。
「グラフ作成」にチェックを入れます。
エクセル ヒストグラム表の自動作成
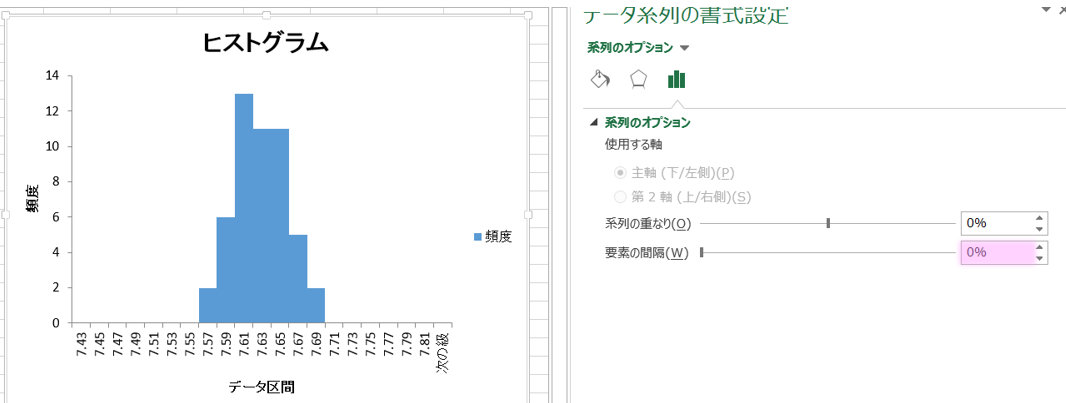
新しいシートに度数表とヒストグラムが作成されます。
ヒストグラムの修正 サイズ&棒間隔
データの系列をダブルクリックして、書式設定を表示、[系列のオプション]を選択して、要素の間隔を「0%」にします。
ヒストグラムの完成です。
超簡単 最新 エクセル2016 ヒストグラム作成
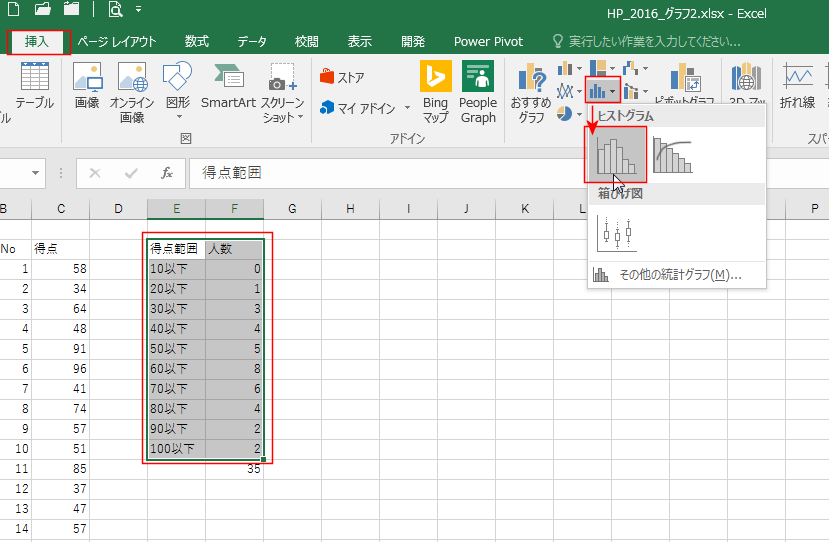
エクセル2016では統計グラフの挿入からヒストグラムを作成することができるようになっています。
Excel 2016 統計グラフによるヒストグラム表の作成
エクセル2016の新機能である「ヒストグラム」を作成する方法の説明です。
データを選択
ヒストグラムにするデータ範囲を選択。
[挿入]タブの[統計グラフの挿入]→[ヒストグラム]を実行。
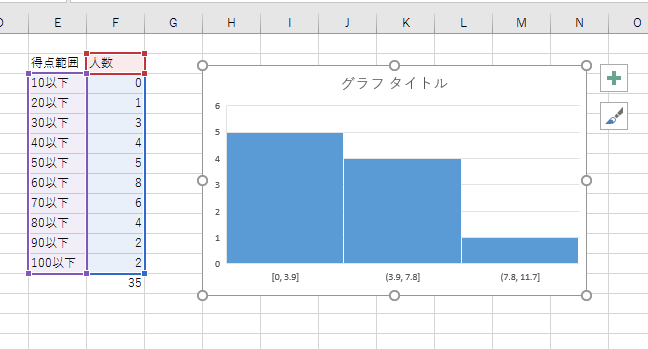
仮のヒストグラム作成
自動的にヒストグラムが作成されるが横軸の区切り方がおかしいので、修正が必要。
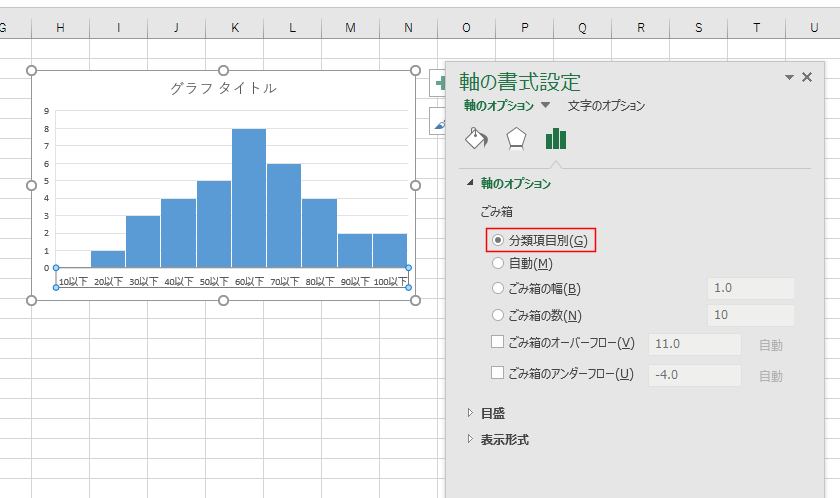
軸の書式設定の変更
横軸ラベルをダブルクリックします。
軸の書式設定 ウィンドウが表示されました。
軸のオプションの『自動』を『分類項目別』を選択し、完成。
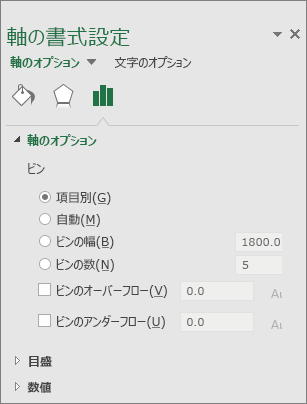
ヒストグラム データービン(bin)の変更
ヒストグラム データービンの設定を変更したい場合は下記を参照してください。
ここで意味しているデータービンとはヒストグラムの区間幅の事です。
自動
ヒストグラムの既定の設定です。
ビンの幅
各範囲のデータ ポイントの数に正の 10 進数を入力します。
ビンの数
ヒストグラムのビンの数を入力します (ビンのオーバーフローとアンダーフローを含む)。
ビンのオーバーフロー
右側のボックスの値を上回るすべての値にビンを作成する場合にオンにします。 値を変更するには、別の 10 進数をボックスに入力します。
ビンのアンダーフロー
右側のボックスの値以下のすべての値にビンを作成する場合にオンにします。 値を変更するには、別の 10 進数をボックスに入力します。
ヒストグラムの見方・活用の仕方
ヒストグラムを作成してみると、データのバラツキの分布状態がひと目でわかります。つまり、ヒストグラムの分布状態および規格値から、データの内容をうかがい知ることができます。
また規格値が与えられているときは,それをヒストグラムに書きこんでみることが大切である。規格値と照らし合わせて満足な状態でなかったときには,もちろん規格値に合うよう努力すべきであるが,一方規格値が決められた根拠を反省してみることも必要である。
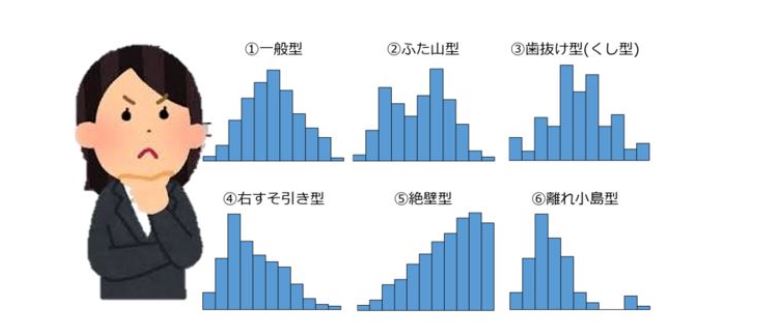
正常な型 ヒストグラム
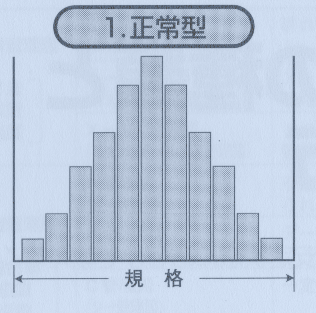 中心部が最も高く、左右対称で釣鐘のような形をしており、バラツキも規格内にあり、問題はなさそうです。
中心部が最も高く、左右対称で釣鐘のような形をしており、バラツキも規格内にあり、問題はなさそうです。
ミダシ型 ヒストグラム
 分布状態はよいが、左右の裾野が規格外に(ミダシている場合。規格外の不適合が混入して
分布状態はよいが、左右の裾野が規格外に(ミダシている場合。規格外の不適合が混入して
おり、改善を行なう必要があります。
同片寄り型 ヒストグラム
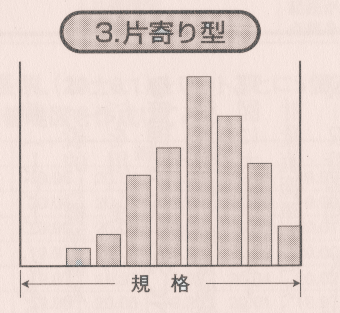 分布状態は正常状態と同じような形をしていますが、中心部が中央からどちらかに片寄り、片寄った側が規格値の限界にきており、規格外の不適合品が出る可能性があります。中心部を中央に持っていく改善が必要です。
分布状態は正常状態と同じような形をしていますが、中心部が中央からどちらかに片寄り、片寄った側が規格値の限界にきており、規格外の不適合品が出る可能性があります。中心部を中央に持っていく改善が必要です。
離れ小島型 ヒストグラム
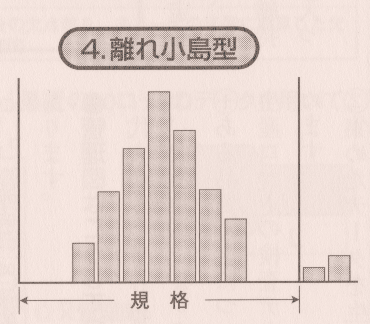 離れたところに一つの山がある場合をいいます。離れ小島の原因は、他の製品や材料の混入、工程での突発事故や測定ミスなどがあり、原因を調査し改善を行なう必要があります。
離れたところに一つの山がある場合をいいます。離れ小島の原因は、他の製品や材料の混入、工程での突発事故や測定ミスなどがあり、原因を調査し改善を行なう必要があります。
ふた山型 ヒストグラム
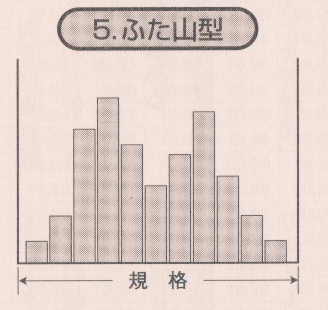 分布の山が二つある場合です。2台の機械で作業した場合や、異なるロットのモノが混入した場合などが考えられます。層別して調べる必要があります。
分布の山が二つある場合です。2台の機械で作業した場合や、異なるロットのモノが混入した場合などが考えられます。層別して調べる必要があります。
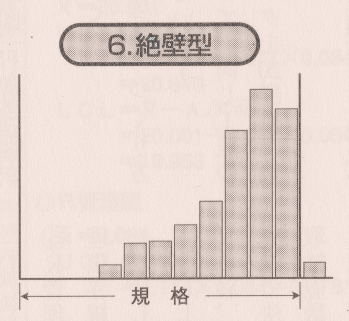
絶壁型 ヒストグラム
歯抜け型 ヒストグラム
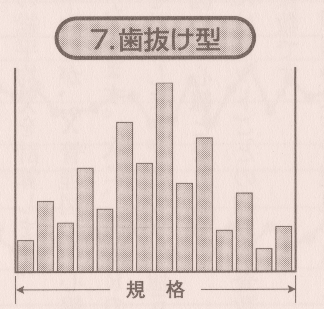 分布の柱がひとつおきに歯抜けになった状態で、測定者の測定目盛りの読み方に癖がある場合や区間幅が不適切な場合に起こります。原因を調査し、改善を行なう必要があります。
分布の柱がひとつおきに歯抜けになった状態で、測定者の測定目盛りの読み方に癖がある場合や区間幅が不適切な場合に起こります。原因を調査し、改善を行なう必要があります。
裾引き型 ヒストグラム
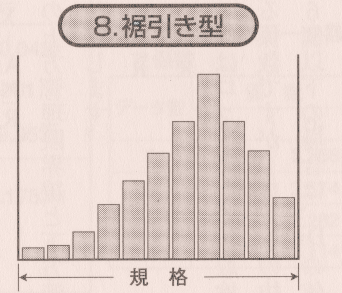 左右対称ではなく、一方が裾を引いた形をしており、原因を調査し、改善をする必要があります。
左右対称ではなく、一方が裾を引いた形をしており、原因を調査し、改善をする必要があります。
関連記事:QC七つ道具
ヒストグラム(度数分布図)Web作成
オンラインでヒストグラム(度数分布図)が作成できるサイトの紹介、現場で簡単にスマホで作成できます。
Easy Histogram ヒストグラム Web作成
ヒストグラムを作りたいデータを Excel からコピーして、このサイトのテキスト欄に貼りつけるだけで作成できます、とても便利です。
関連サイト:Easy Histogram
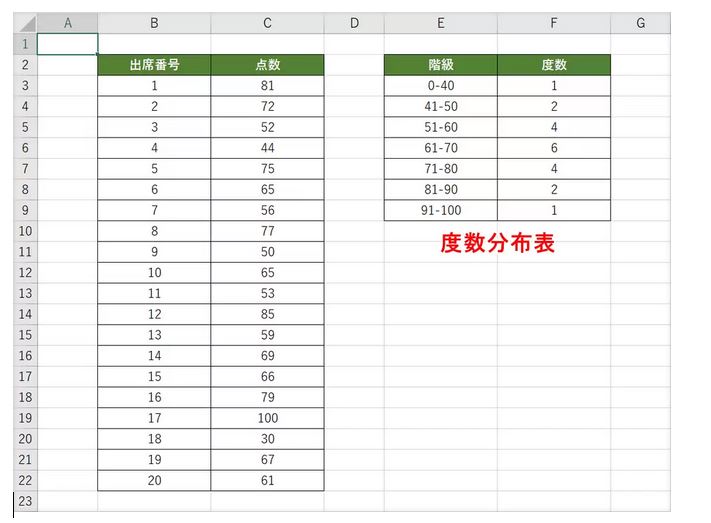
例として下表の20人のテストの点数をWebで作成します。
該当サイトの欄に入力した結果が下記です。
実際の使用法は下記のサイトを参照してください。
参照サイト:簡単にヒストグラムを作成できるサイトを作った
Google スプレッドシート ヒストグラム Web作成
エクセルを使う方法で、手軽にヒストグラムが作れます。
グラフをホームページやブログに埋め込んでインターネットに公開することもできます。
方法はGoogleスプレッドシートでグラフ表示用のHTMLコードを生成し、ホームページやブログのHTMLの中に手動で埋め込みます。
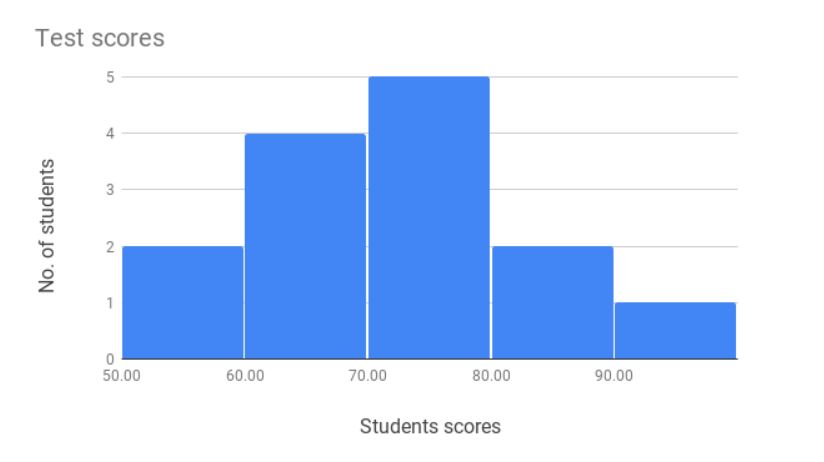
下記がGoogleスプレッドシートで作成したヒストグラム(度数分布図)のサンプルです。
実際に作成方法は下記のサイトを参照してください。
関連サイト:Google スプレッドシート ヒストグラム
ヒストグラム 事例
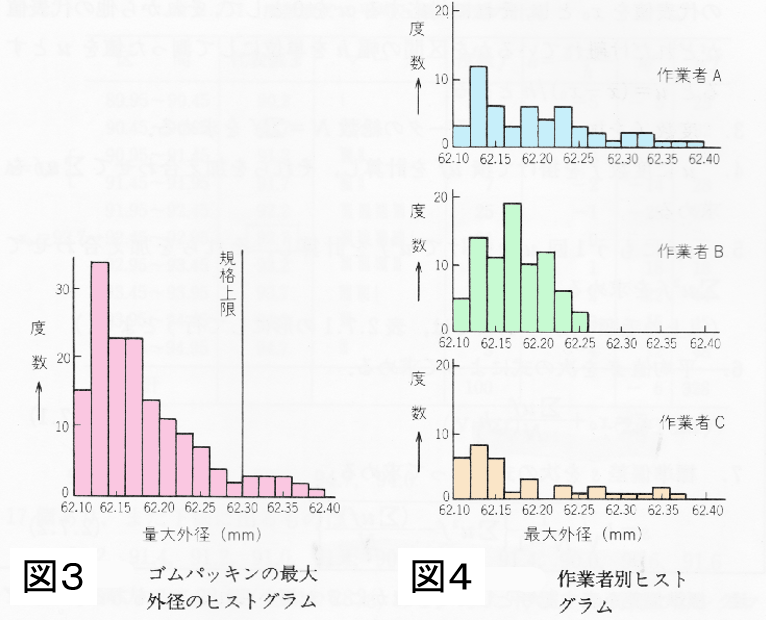
例 ゴム製パッキンの外径寸法の規格は62.1±0.2mmであるが,外径寸法による不良がでるので,最近の製品154個についてヒストグラムを書いたところ図3とおりであった。成型はA,B,C3人の作業者が行っているが,これが径のばらつきに最も影響すると思われたので,このデータを作業者別に層別してヒストグラムを書いたところ図4のようになった。
Bのばらつきが最も少なく,A,Cは大きいことがわかったが,この順序は作業者の熟練度と必ずしも一致していないので,3人の作業方法を比較してみた。
その結果,型から取り出すのを容易にするための薬剤を塗るのに,Aは型の両面,Bは型の下面のみ,Cは型の上面のみと言うようにそれぞれ塗り方が異なっているのがわかった。AとCにもBと同じ作業方法でやらせたら,ばらつきが小さくなることがわかったので,Bの方法を標準として定めた。
ヒストグラムによる工程解析手順
目的:
特性項目、ロットの種類を入力、特に目的については何の為に行うか良く検討してから測定、解析すること。
・測定前に関連部署と調整を行うこと。(リーダー、設計、品質管理)
サンプリング
・サンプリングを工程監督者、作業者に依頼するときは目的を理解して貰う為に、シンプルな文書にて目的、サンプリンの方法、個数、期限を記入し依頼すること。
*サンプルがいい加減なサンプルならいくらどんな統計ソフトを駆使しても良い解析はできない!
・工程に依頼する際はサンプリングに立会い、現場の状態を確認すること。
測定
・測定を工程監督者、測定者に依頼するときは目的を理解して貰う為に、シンプルな文書にて
目的、測定方法、個数、期限を記入し依頼すること。
その際、事前にサンプルに後で履歴がわかるようにナンバーを記入しておくこと。
・測定に依頼する際は測定に立会い、現場の状態を確認すること。
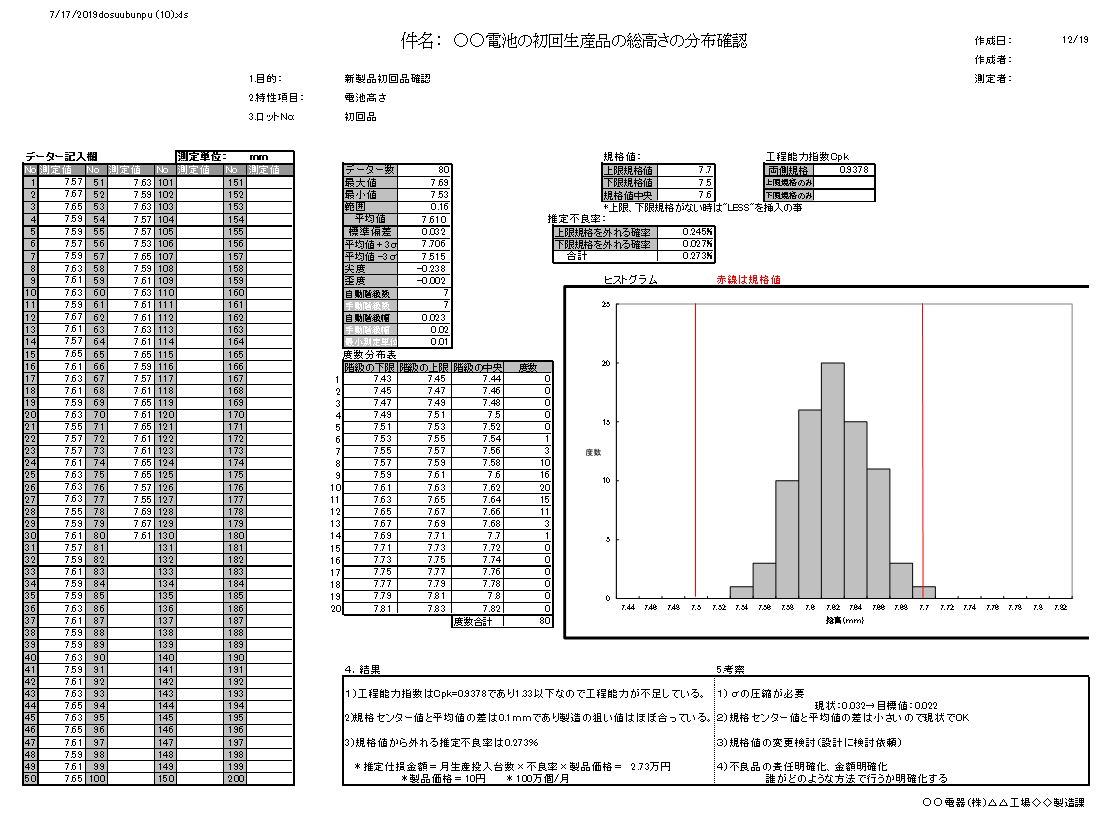
Excelを起動してファイル名:度数分布表を開く。
下記にエクセルで作成したヒストグラム(度数分布図)があります、ご自由にダウンロードしてご使用ください。
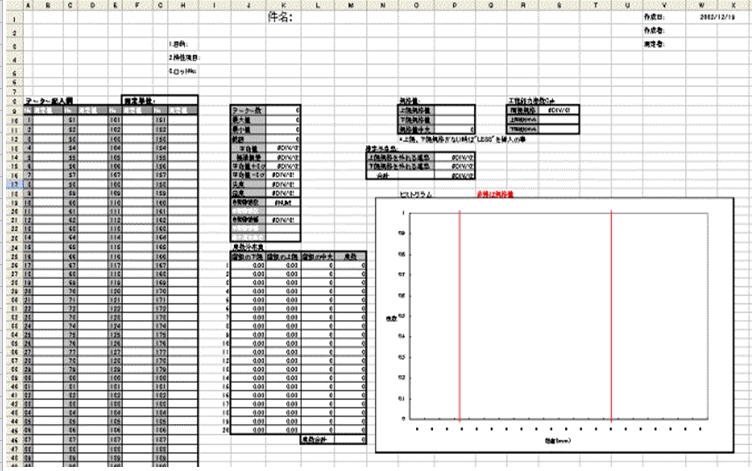
エクセル ヒストグラム作成の方法
空欄を入力する
件名、目的、特性項目、ロットの種類を入力をする。
データー記入
・測定データーをハンドにて入力する。
*自動的に基本統計量が更新される。(データー数、最大値、最小値etc)
・測定単位を入力する。
度数分布表の作成
・階級数:度数分布表を作成するために自動階級数を参考に手動階級数を入力する。
自動階級数は『スタージェスの公式』より算出。
| データー数 | 適当な階級数 |
| 50~100 | 6~10 |
| 100~250 | 7~12 |
| 250以上 | 10~20 |
・階級 自動階級幅を参考に手動階級幅を入力する。
最小測定単位の倍数で入力するとヒストグラムが見やすい。
・手動階級数、手動階級幅を入力すると自動的に度数分布表が作成される。
相対度数の自動算出
それぞれの階級の度数を度数の合計で割ったものをそれぞれの階級の相対度数といいます。
それぞれの度数を,度数の合計100で割っています。
ヒストグラム エクセル表では相対度数は自動的に計算されます。
工程能力指数の把握
・両側規格があるとき:上限規格値、下限規格値を入力する。
・下限規格のみ:上限規格に”LESS”を入力し、次に下限規格値を入力する。
・上限規格のみ:下限規格に”LESS”を入力し、次に上限規格値を入力する。
・工程能力指数Cpkが自動計算に計算される。
規格値の記入
上限、下限規格値線を記入して工程の状態が目でもわかるようにする。
結果記入
数値をもとにデーターで表現する。
工程能力指数Cpkの計算式 |統計関数
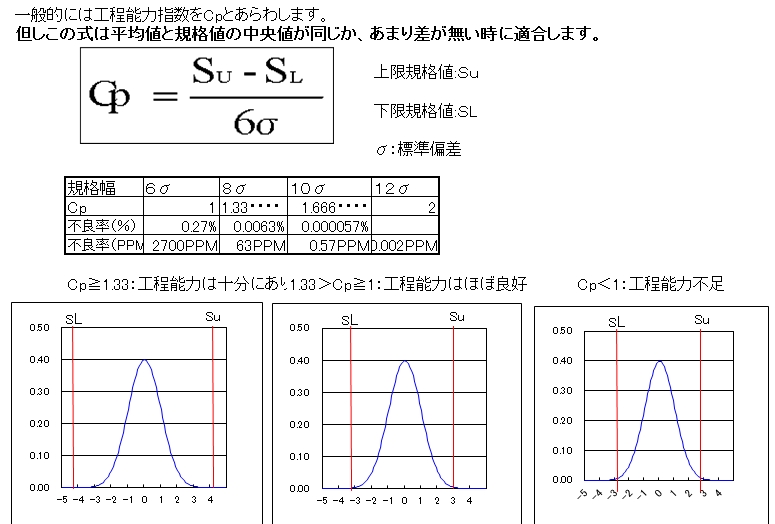
Cp≧1.33:工程能力は十分 1.33>Cp≧1:工程能力はほぼ良好 Cp<1:工程能力不足
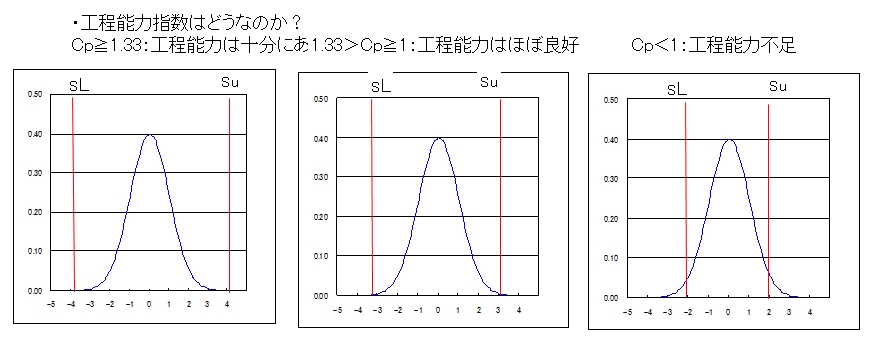
工程能力指数Cpk
・平均値は規格センターと比較してどうなのか?
・平均値は過去、又は別なロットと比較してどうか?
・標準偏差は過去、又は別なロットと比較してどうか?
・推定不良率及び仕損金額は?
考察: 改善の目標を数値化し明確にする。
・標準偏差をいくら圧縮するか?
・平均値をどのくらい規格中央値に近づけられるか?
・不良品の責任部署の明確化と処理の明確化。
工程能力指数の説明
工程から作り出された製品の品質が規格に対してどのようにな状態になっているかを評価する
指数として工程能力指数があります。
これは工程の生産量、能率を表す工程能力指数とは違います。
ここで言う工程能力とは規格に対する工程のバラツキの大きさを示す能力のことです。
1)工程能力指数Cpついて
「工程能力指数」とは「ある特性において規格幅を6σで割った値」で定義されます。
6σとはσの6倍すなわち標準偏差の6倍の意味です。
工程能力指数Cpkの判定
工程能力指数Cpkついて
現場での工程では平均値と規格値の中央値が同じ場合は少ないので上記の工程能力指数では正しい工程能力指数が得られないために下記の式で工程能力指数を求めます。
その際の工程能力指数はCpkで表します。

片側規格のCpkついて
上限規格のみの場合は下記の式より求まります
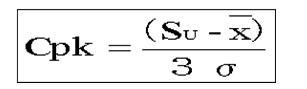
下限規格のみの場合は下記の式より求まります
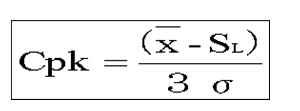
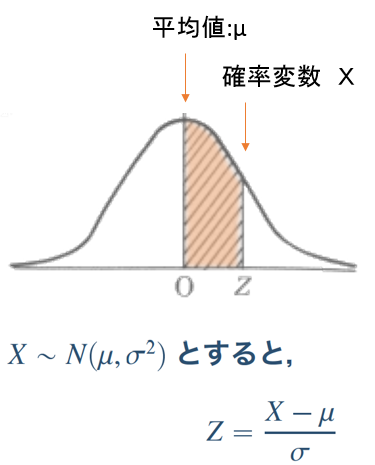
標準正規分布表とヒストグラム
平均が0,標準偏差が1となる正規分布のことを標準正規分布といいます。
そしてその値を一覧にしたものが正規分布表です。
図で簡単に説明すると下記のような図になります。
表の中の値は、全てのの面積を1.0とした場合、Z=0からZまでの面積を示します。
例としてZ=2.00の場合は『0.4772』で、斜線の部分の面積が全体の47.72%です。
よって、ヒストグラムで算出した標準偏差σから変数Xの占有率が簡単に求める事ができます。
標準正規分布表
| Z | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | .0000 | .0040 | .0080 | .0120 | .0160 | .0199 | .0239 | .0279 | .0319 | .0359 |
| 0.1 | .0398 | .0438 | .0478 | .0517 | .0557 | .0596 | .0636 | .0675 | .0714 | .0753 |
| 0.2 | .0793 | .0832 | .0871 | .0910 | .0948 | .0987 | .1026 | .1064 | .1103 | .1141 |
| 0.3 | .1179 | .1217 | .1255 | .1293 | .1331 | .1368 | .1406 | .1443 | .1480 | .1517 |
| 0.4 | .1554 | .1591 | .1628 | .1664 | .1700 | .1736 | .1772 | .1808 | .1844 | .1879 |
| 0.5 | .1915 | .1950 | .1985 | .2019 | .2054 | .2088 | .2123 | .2157 | .2190 | .2224 |
| 0.6 | .2257 | .2291 | .2324 | .2357 | .2389 | .2422 | .2454 | .2486 | .2517 | .2549 |
| 0.7 | .2580 | .2611 | .2642 | .2673 | .2704 | .2734 | .2764 | .2794 | .2823 | .2852 |
| 0.8 | .2881 | .2910 | .2939 | .2967 | .2995 | .3023 | .3051 | .3078 | .3106 | .3133 |
| 0.9 | .3159 | .3186 | .3212 | .3238 | .3264 | .3289 | .3315 | .3340 | .3365 | .3389 |
| 1.0 | .3413 | .3438 | .3461 | .3485 | .3508 | .3531 | .3554 | .3577 | .3599 | .3621 |
| 1.1 | .3643 | .3665 | .3686 | .3708 | .3729 | .3749 | .3770 | .3790 | .3810 | .3830 |
| 1.2 | .3849 | .3869 | .3888 | .3907 | .3925 | .3944 | .3962 | .3980 | .3997 | .4015 |
| 1.3 | .4032 | .4049 | .4066 | .4082 | .4099 | .4115 | .4131 | .4147 | .4162 | .4177 |
| 1.4 | .4192 | .4207 | .4222 | .4236 | .4251 | .4265 | .4279 | .4292 | .4306 | .4319 |
| 1.5 | .4332 | .4345 | .4357 | .4370 | .4382 | .4394 | .4406 | .4418 | .4429 | .4441 |
| 1.6 | .4452 | .4463 | .4474 | .4484 | .4495 | .4505 | .4515 | .4525 | .4535 | .4545 |
| 1.7 | .4554 | .4564 | .4573 | .4582 | .4591 | .4599 | .4608 | .4616 | .4625 | .4633 |
| 1.8 | .4641 | .4649 | .4656 | .4664 | .4671 | .4678 | .4686 | .4693 | .4699 | .4706 |
| 1.9 | .4713 | .4719 | .4726 | .4732 | .4738 | .4744 | .4750 | .4756 | .4761 | .4767 |
| 2.0 | .4772 | .4778 | .4783 | .4788 | .4793 | .4798 | .4803 | .4808 | .4812 | .4817 |
| 2.1 | .4821 | .4826 | .4830 | .4834 | .4838 | .4842 | .4846 | .4850 | .4854 | .4857 |
| 2.2 | .4861 | .4864 | .4868 | .4871 | .4875 | .4878 | .4881 | .4884 | .4887 | .4890 |
| 2.3 | .4893 | .4896 | .4898 | .4901 | .4904 | .4906 | .4909 | .4911 | .4913 | .4916 |
| 2.4 | .4918 | .4920 | .4922 | .4925 | .4927 | .4929 | .4931 | .4932 | .4934 | .4936 |
| 2.5 | .4938 | .4940 | .4941 | .4943 | .4945 | .4946 | .4948 | .4949 | .4951 | .4952 |
| 2.6 | .4953 | .4955 | .4956 | .4957 | .4959 | .4960 | .4961 | .4962 | .4963 | .4964 |
| 2.7 | .4965 | .4966 | .4967 | .4968 | .4969 | .4970 | .4971 | .4972 | .4973 | .4974 |
| 2.8 | .4974 | .4975 | .4976 | .4977 | .4977 | .4978 | .4979 | .4979 | .4980 | .4981 |
| 2.9 | .4981 | .4982 | .4982 | .4983 | .4984 | .4984 | .4985 | .4985 | .4986 | .4986 |
| 3.0 | .4987 | .4987 | .4987 | .4988 | .4988 | .4989 | .4989 | .4989 | .4990 | .4990 |
| 3.1 | .4990 | .4991 | .4991 | .4991 | .4992 | .4992 | .4992 | .4992 | .4993 | .4993 |
| 3.2 | .4993 | .4993 | .4994 | .4994 | .4994 | .4994 | .4994 | .4995 | .4995 | .4995 |
| 3.3 | .4995 | .4995 | .4995 | .4996 | .4996 | .4996 | .4996 | .4996 | .4996 | .4997 |
| 3.4 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4998 |
| 3.5 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 |
| 3.6 | .4998 | .4998 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 |
| 3.7 | .4999 | .4999 | .4999 | .4999 | .49991 | .49992 | .49992 | .49992 | .49992 | .49992 |
| 3.8 | .49993 | .49993 | .49993 | .49994 | .49994 | .49994 | .49994 | .49995 | .49995 | .49995 |
| 3.9 | .49995 | .49995 | .49996 | .49996 | .49996 | .49996 | .49996 | .49996 | .49997 | .49997 |
| 4.0 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 |
| 4.1 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 |
| 4.2 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.3 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.4 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.5 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 |
| 4.6 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 |
| 4.7 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.8 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.9 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 |
| 5.0 | .499997 |
エクセル STDEVA 関数と STDEV 関数の説明
ここで紹介する例は、下記のようなサンプル データに基づいています。
1. セルA1 に「 1 」と入力します。
2. セルA2 に「 2 」と入力します。
3. セルA3 に「 6 」と入力します。
4. セルA4 に「 TRUE 」と入力します。
( 大文字・小文字どちらで入力しても自動的に変換されます。 )
5. セルA5 に「 hello 」と入力します。
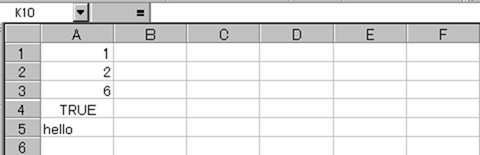
STDEV 関数が、標本内の数値のみを対象にして標準偏差予測を返すのに対して、STDEVA 関数は、標本内の数値、文字列、および論理値を含めて、標準偏差予測を返します。
エクセル 標準偏差の説明
母集団の標本数が少なく全ての測定データーがある時は下記の式から母集団の標準偏差が計算される。
母標準偏差 σ=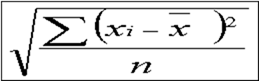
*エクセルのSTDEVP関数で求まる。
しかし、現場においては全ての標本数の測定は時間を要しコストが要す為、n個のサンプル数で母集団の標準偏差の推定を行う。
その際に上記の式(nで割った式)で求めた値は真の母標準偏差より小さくなる傾向がある為、下記の式にて標本に基づいて計算した母集団の標準偏差の推定値を求めます。
(但し、この式でも真の母集団の標準偏差よりまだ小さくなる傾向があります)
標本標準偏差 =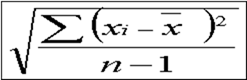
*ExcelのSTDEV関数で求まる。
より正確な母集団の標準偏差を計算をした時は下記の表(母標準偏差の不偏推定係数)からサンプル数に適合した不偏推定係数をnで割って求めたσに掛けて求めることができます。
しかしサンプル数がn=50以上にあればn-1で割って求めたσと真の母標準偏差との差は少なくなり、実用上、問題なく使用できます。

尖度説明
ある2つの集団のデーター分布をグラフで表示してみるとグラフの曲線が狭くとがった形状となったり扁平な曲線になったりしてその分布の型はかなり異なることがある。
その分布の型を表現する数量として尖度(せんど:Kurtosis)と歪度(わいど:Skewness)がある。
尖度の定義
尖度はグラフの尖り度合いを示す数量で平均値をXbar標準偏差をσ、尖度をKとすると次の式で求まる。
となります。標本の尖度を Excel で求めるには,上の定義通り計算させるしかありませんが,尖度の不偏推定値なら KURT関数を使用することができます。
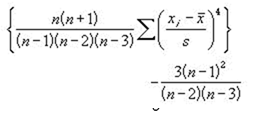
尖度の評価
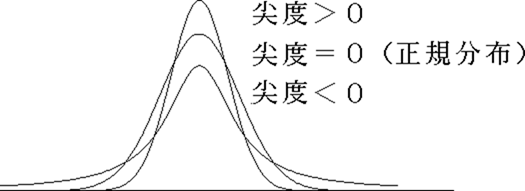
尖度の評価

具体事例
下記式より尖度を求める。
結果:2.368679
(3引き尖度は-0.63132101)
Excel関数KURTを使用して計算。
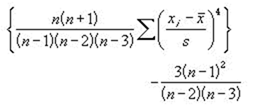
尖度の定義
歪度とは、分布の平均値周辺での両側の非対称度を表す値です。正の歪度は対称となる分布が
正の方向へ伸びる非対称な側を持つことを示し、負の歪度は対称となる分布が負の方向へ伸びる非対称な側を持つことを示します。
歪度はグラフのひずみ度合いを示す数量で平均値をXbar標準偏差をσ、尖度をSとすると次の式で求まる。
となります。標本の歪度を Excel で求めるには,上の定義通り計算させるしかありませんが歪度の不偏推定値ならSKEW関数を使用することができます。
下記が式です。
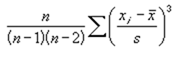
歪度の評価
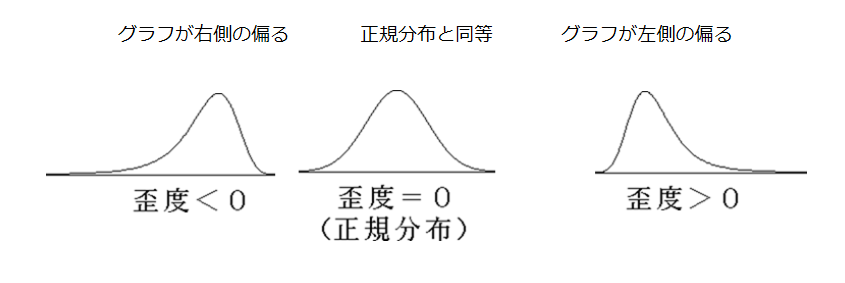
歪度の評価
具体事例
下記式より尖度を求める。
結果:0.303193
*左にグラフが偏っている
Excel関数SKEWを使用して計算。
参考文献:QSS-普通科テキスト 統計的手法 日本規格協会
まとめ
ヒストグラムは、大量のデータを視覚的に表現し、その特徴を簡単に捉えることができる便利なツールです。様々な分野で活用されており、データ分析の基礎として知っておくべきグラフの一つです。
『ChatGPTでヒストグラムを作成する!【図解】』については下記の記事を参照 願いします。

関連キーワード:
#ヒストグラム
#度数分布図
#データ分析
#統計学
#Excel ヒストグラム
slideshare 無料ダウンロード資料(PDF)
パワーポイントで作成した資料です。
おすすめ QC七つ道具 参考文献:



























コメント
カタヨリKの計算式が間違っています。
分子は、SU+SLぽいです
連絡有難うございします。
統計の本をそのまま、記載したので間違っているかどうかは不明ですが
他サイトでもどうような記載をしていました。
工程能力指数 (Cp,Cpk) その4
以上、宜しくお願いします。