実験計画法

実験計画法(DoE)　design  of 　experiments    【イラスト図解】

英語：design  of 　experiments 　　　　　　　　　　　　　　　中国語：实验设计法

実験計画法(DoE)とは

実験計画法(DoE)とは，取り上げる対象の結果とそれに影響を与えると思われる要因の関係を調べるために，時間面，経済面などの制約を考慮しながら実験によりデータを得て，それを解析するための方法である．

物理学，化学における科学的精密実験では，実験を行う条件などに気を配ることで結果のばらつきができる限り　小さくするようにする．すなわち，実験の誤差が存在しなくなることを目指す．

　これに対して実験計画法(DoE)では，適切に実験が行われた場合の実験誤差の存在は認めたうえで，数理統計学の力により種々の推論を行う．

実験計画法は，フィッシャー(Ｒ.Ａ.Fisher)によって農事試験での応用を目的に開発された．農事試験の場合には，天候，農場，温度，水分など結果に影響を与える要因が複数存在する．

また，これらの条件を厳密に一定に保つことは現実的に不可能であり，実験結果にばらつきが存在することを認めざるを得ない．さらに農事試験では，品種，育成方法など，複数の処理の中から収穫高の高いものを，ばらつきの存在を認めたうえで見いだすことが必要となる．このような農事試験に対する要請が，実験計画法が生まれるきっかけとなった．

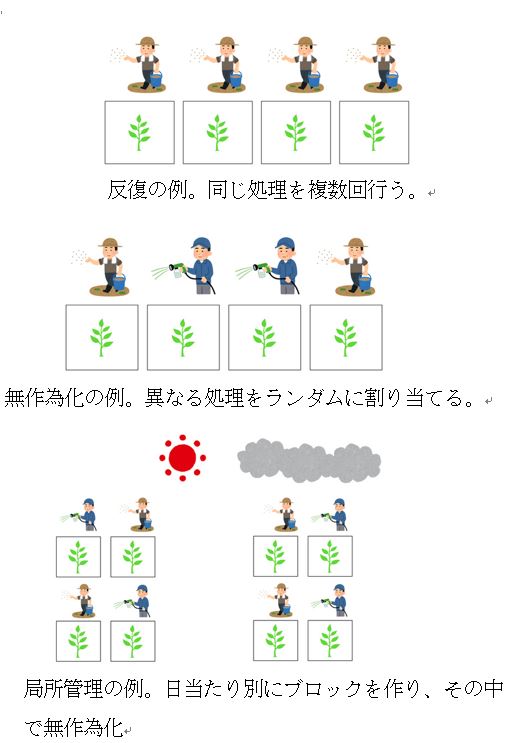
実験を行う際のフィッシャーの３原則　とは，①反復(replication)，②ランダム化，無作為化(randomization),③局所管理(local control)である．

実験結果の変動が偶然的なものなのか，あるいは処理の違いによって生じているのかを評価するためには，実験の誤差によるばらつきを評価する必要があり，

①は誤差による変動
の評価を可能にする．特定の処理について空間的，時間的に同一の条件で実験を
繰り返し続けると，結果の処理間の変動が処理によるものなのか誤差によるもの
なのかが区別できなくなるので，

②を行い処理による変動以外を確率的な誤差に転化する．この転化は，実験により得たデータを統計解析することの正当性を保証する．実験の場全体をランダム化することを考えると，それが経済的，空間的制約により困難な場合や，誤差が大きくなる場合には，

③が処理間の比較に有効である．

農事試験から始まった実験計画法は種々の分野に，それぞれの分野の特徴に応じて展開されている．

医学の臨床試験においては，例えば実験のランダム化か人道的見地から議論され，これを考慮した形で種々の方法が検討されている．

また教育，心理学の分野では，実験の反復の可否などが議論されている．さらに工業の分野では，生産現場での不適合品低減のみならず，設計，研究開発段階へ展開や，市場調査への応用など，幅広く用いられるべく種々の方法が議論されている．

実験計画法の中身も，その適用分野に応じて種々の方向に発展している．ランダム化の困難さに対応するための分割法や，局所管理を実現するためのブロック計画がその例として挙げられる．

また，ブロック計画は，代数学と連携し数学的な取り扱いの意味でも発展している．多因子の場合には実験回数が膨大になるので，これを避けるために一部実施計画が考案されている．

線点図，直交配列表は一部実施計画の構成に便利である．

比較的近年に目を移すと，田ロメソッドでは使用者の環境条件の変動に対して頑健な設計を実現するための方法など独自の方法が発展している．

応答曲面法は，化学プロセスなど量的な因子が興味の対象となる場で生まれ，応答と因子の関係を因子の多項式などで効率的に表現するための方法を目指すなど発展している．

さらに配合計画は，物質の配合割合を決めるときにはその合計が常に100％となることを考慮して構成されている．

そして，コンピュータの発展に伴い，シミュレーションなどに適した実験計画の構成や，理論上のものだった最適計画の実務上への応用が議論されている．

実験計画により得られたデータの解析は，基本的には，分散分析により応答の平方和を要因ごとに分解し，それを用いて要因の効果について吟味される．

このデータ解析においては，因子の水準によって応答の期待値が決まり，応答の観測値はその期待値と誤差との和で表されるという加法モデルが用いられる．

また誤差について，独立に正規分布に従うことが仮定されることが多い．データの解析時にはモデルの当てはまりを吟味し，このような一般的なモデルを越えて対象により即したモデルを用いた解析の必要性を検討する必要がある．

さらに一歩踏み込んで，実験計画法を構成する上でも取り上げた対象に即したモデルによる解析がより効率的に行えるようにすることは，計画段階で重要なこととなる．

品質管理はシューハートが管理図を提案したのが起源とされていることからもわかるとおり，その中核にはデータを収集し，解析し，事実に基づく管理を行うことがある.

TQMにおいてもその基本は品質保証で，支えているのはデータの収集・解析である．さらに1990年代後半より米国を中心に注目されたシックスシグマにおいても，その教育プログラムから明らかなように，データの収集・解析が中核にある.

実験計画法は，データ解析法とあわせ，品質管理の中核について重要な役割を演じる．

引用先：クォリティーマネジメント用語辞典　日本規格協会

 

「実験計画法」の目的

実験計画法の目的とは、「効率的で客観的な結論を得られるように実験を計画すること」です。

特に、品質管理のお仕事をされている方からすれば、「実験数を減らすために利用するもの」なのかと考えてしまいがちですが、実験計画法の本質は、「問題を解決するために、データをどういった方法で集めるのか、計画を立てる方法」です。そのため、単純に実験数を減らすという目的ではありません。

通常であれば、実験を行っていく場合には、「要因」などを複数の種類で設定して、それらを一つ一つ組み合わせて実験を進めていきます。そのやり方が基本的に正しいのですが、手間ばかりが掛かってきてしまいます。効率的に実験・試験を行い、進めるために実験計画法があり、複数要因を一緒に実験・試験をしていける方法として、分散分析があります。

分散分析とは、比較したいグループが3つ以上存在する場合に使うことのできる統計手法のことで、3つのグループ間の中でデータにどのような差が出てくるのかを検定します。

Fisherの3原則

実験には必ず誤差が伴うため、「実験誤差をできるだけ小さくする」とともに「実験誤差の大きさを推定する」ことが必要となる。そのためには、Fisherにより提唱された以下の3原則を満たすような実験の配置が望ましい。

反復(Replication)
無作為化(Randomization)
局所管理(Local control)

「反復」とは、同じ処理を複数の実験単位に配置することをいう。具体的には、異なる複数の被験者に同じ薬剤を服用してもらう、複数の区画で同じ量の施肥を行う、などである。反復を行うことで、同じ処理を行った場合におこる偶然的な誤差の大きさを推定することができる（データから標本分散を計算できる）。また、反復の数を増やすことによって誤差を小さくすることができる（サンプルサイズが増えると標本平均のばらつきが小さくなる）。なお、同じ実験単位からあたかも反復であるかのように複数のデータを観測する行為は「擬似反復」として知られており、このようなデータを用いると誤差を過小評価することにつながる。

「無作為化」は、結果にバイアスを生じさせるような因子の影響を取り除くために行われる。例えば2種類の薬剤の効果を比較する臨床試験であれば、一方の薬剤が重症者ばかりに、他方の薬剤が軽症者ばかりに投与されたとしたら、薬剤の純粋な効果を評価するのは難しいことが想像できる。そのため、処理（この例では2種類の薬剤）の割り当てを無作為に行い、両方の処理の間で結果に影響するような他の因子が偏らないようにする必要がある。

反復数を増やしたり多くの種類の処理を行いたい場合、たくさんの実験単位が必要となってくる。すると、例えば農事試験では多くの作物を植えるための広い農地を準備しないといけないが、農地の肥沃度の違いが系統的な誤差（バイアス）を生じさせる可能性がある。このような系統誤差の原因と考えられるものを「ブロック」として分割し、各ブロック内で処理の無作為化を行うことにより、系統誤差の影響を除くことができる。この方法を「局所管理」という。臨床試験の場合には、被験者間の誤差が大きくなりがちであるため、被験者をブロックとし、各被験者にランダムな順番で異なる試験治療を実施するような研究計画が用いられることがある（「クロスオーバー計画」と呼ばれる）。

 

実験計画法」の利点

実験計画法の最大の利点は、結果として「試験回数を減らすこと」ができる点です。また、データの分析結果としては、条件の内容がどの程度関りがあるのかを数値データで結果が分かるという点も挙げられます。

（１）開発サイクルの短縮

実験計画は、新機能や他社を圧倒する新技術開発を目指す時に、そうした技術が市場投入後に品質問題が起きないように合理的に検討出来ます。企業は、イノベーションを目指し新しい顧客価値を生み出す独自開発に積極的に取り組むことができるようになるでしょう。

実験計画は、従来の技術が類似製品の開発にも応用できるので、開発にかかる工数を削減できます。そして、開発段階での品質問題が大幅に改善され信頼性の向上につながります。

実験計画法の欠点

実験計画法の欠点として、水準を等間隔に設定して実験を行わないと以下の3つの問題が発生します。

問題1：効率の悪化

3水準を行う実験では、1水準と2水準を殆ど等しい値に設定してしまうと、得られる結果が2水準の実験と殆ど変わらないという悲惨な状況になってしまう可能性もあります。

問題2：計算の煩雑化

多水準（複数）の因子で、直交多項式による分解を使って１次効果や２次効果を求める実験の際に、計算がとても煩雑になってしまうケースもあります。この時に使用する係数は、等間隔の場合には、直交多項式の表に載っている値がそのまま使えますが、等間隔でない場合には、自分で計算して求めないといけない事態になることもあります。

問題3：判断ミスの原因

不当間隔であることを忘れてしまい、等間隔の要因図式を書いてしまったり、等間隔の公式を使用して分析を行ってしまうなどのミスをしてしまうこともあります。

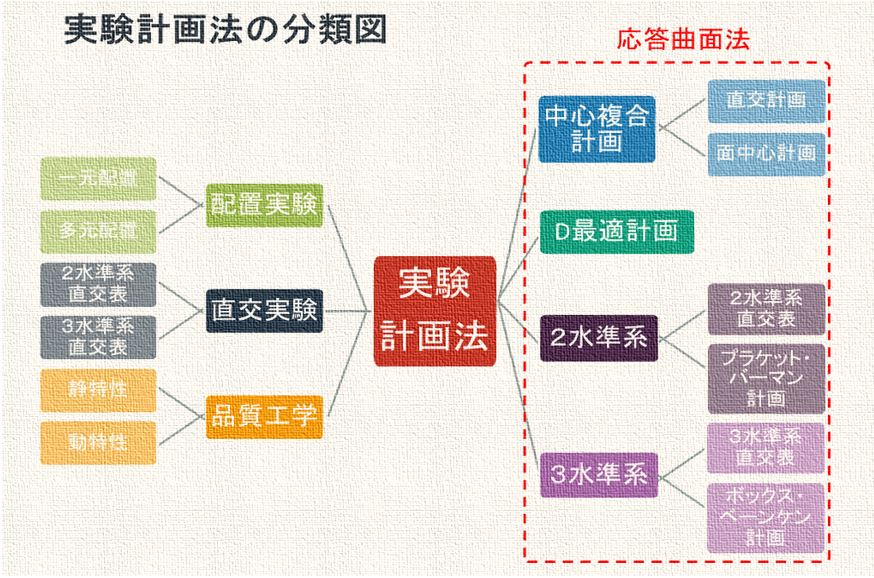
実験計画法の分類図

下記が実験計画法の分類図です。

実験計画法と言っても計画手法は色々あります。