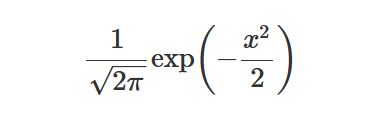- 正規分布 normal distribution 【イラスト図解】
正規分布 normal distribution 【イラスト図解】
英語:normal distribution 中国語:正态分布
正規分布とは
「確率密度関数が∫(x)=1/σ√2π exp[-1/2(x-μ/σ)²]
-∞くxく∞
で与えられる連続変数の分布.
備考:正規分布は,平均μと分散σ2によって定まる.記号N(μ,(σ2)で表すことが多い.」 (Z 8101-1)
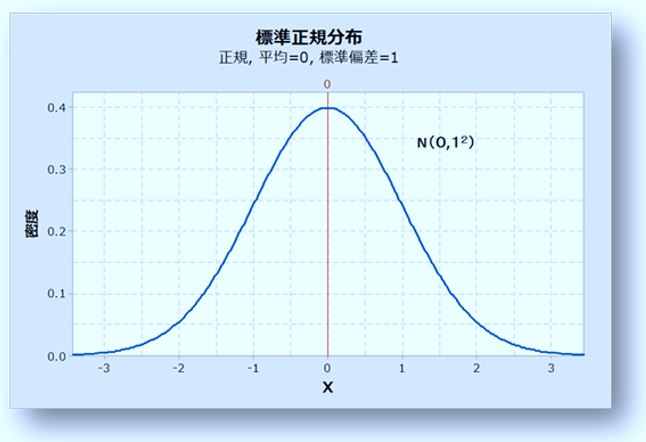
特にN(0,1²)の場合,標準正規分布という.
中心極限定理より,独立な確率変数の和の極限分布は,正規分布に従うことなどから,理論上でも実用上でも殼も重要な分布であり,計量値の検定,推定の多くは正規分布に従う母集団からの標本であることに基礎をおいている.
ガウス(K.F.Gauss)が測定の中に含まれる誤差の理論を説明することに用いたことから,ガウス分布(Laplace Gauss distribution)とも呼ばれる.
引用先:クォリティーマネジメント用語辞典 日本規格協会
わかりやすく 正規分布(ガウス分布)
正規分布(又の名を”ガウス分布” )は形が鐘の形に似ているため、正規分布が描く曲線のことをベルカーブとも呼びます。
統計学を学ぶ上で正規分布が重要なのは自然現象や社会現象には、正規分布に従うものが多くあるからです。
つまり“母集団の分布にかかわらず、母集団から抽出された標本の数が十分に多い場合、標本平均の分布は正規分布に従う”といった性質 中心極限定理がある為です。
中心極限定理が存在するため、数多くの統計手法では、データが正規分布に従うと仮定が用いられます。
正規分布の特徴を挙げると、以下の点を挙げることができます。
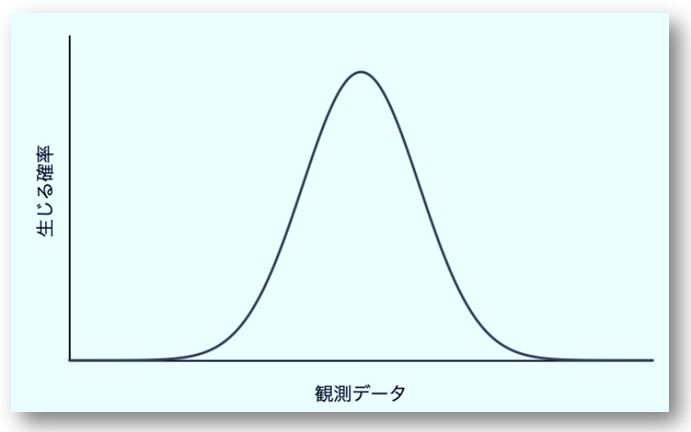
左右対称である
平均の観測データが生じる確率が最も大きい
平均から離れるほど生じる確率は小さくなる
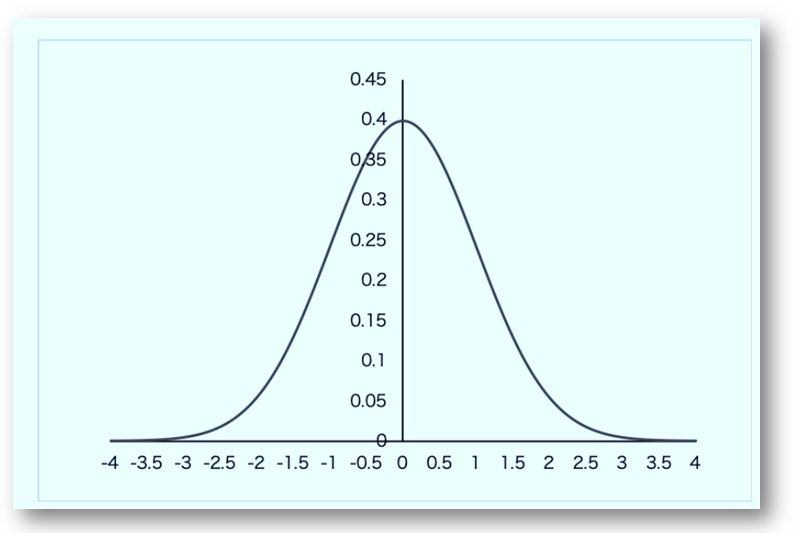
下図の横軸は観測データ(確率変数)を、縦軸はその値が生じる確率(確率密度)を表しています。
正規分布を考えた人は誰
指数関数の一つである正規分布の関数そのものはド・モアブルによって18世紀前半に導かれていました.
ベルヌーイの著書『推測法』(1713)を読んだド・モアブルは,ベルヌーイの提唱する二項分布の回数nに関する極限分布について考察を重ね,1738年に出版された著書『偶然論』の中でその結果を公表しました.
ド・モアブルは二項分布をする確率変数xに関してnが無限大に発散したとき,xの極限分布は
という指数関数によって与えられることを証明しました.この指数関数こそ後に正規分布(normal distribution)とよばれることになる確率分布の誕生が誕生しました。
正規分布(ガウス分布)の性質 わかりやすく
正規分布の性質として重要なことは2つです。
正規分布の形は平均と標準偏差(データのバラツキ)で決まる。
標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かる
正規分布(ガウス分布)のグラフの形:平均と標準偏差で決まる
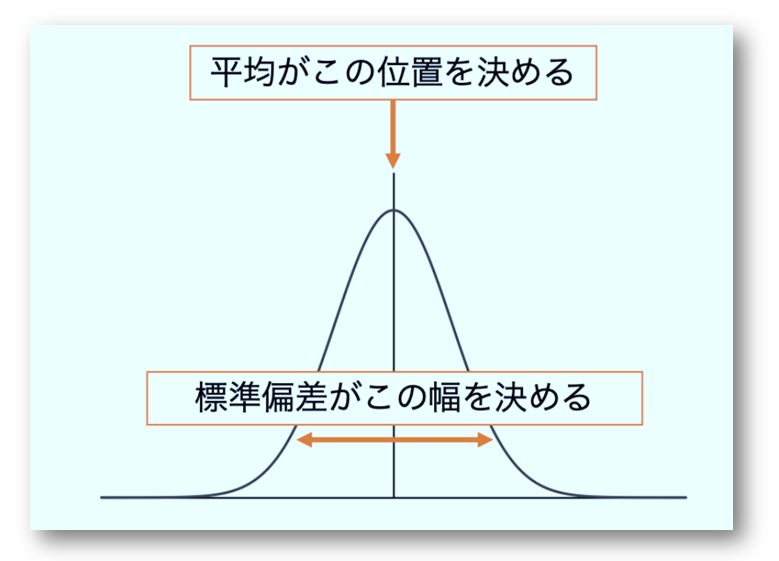
正規分布の形は平均と標準偏差(データのバラツキ)で決定。
平均値は正規分布の中心の位置を決めます、標準偏差は正規分布の左右の広がり幅を決めます。
正規分布を式は下記のとおり。
正規分布の標準偏差:範囲にどれくらいの観測データが含まれいるかが分かる
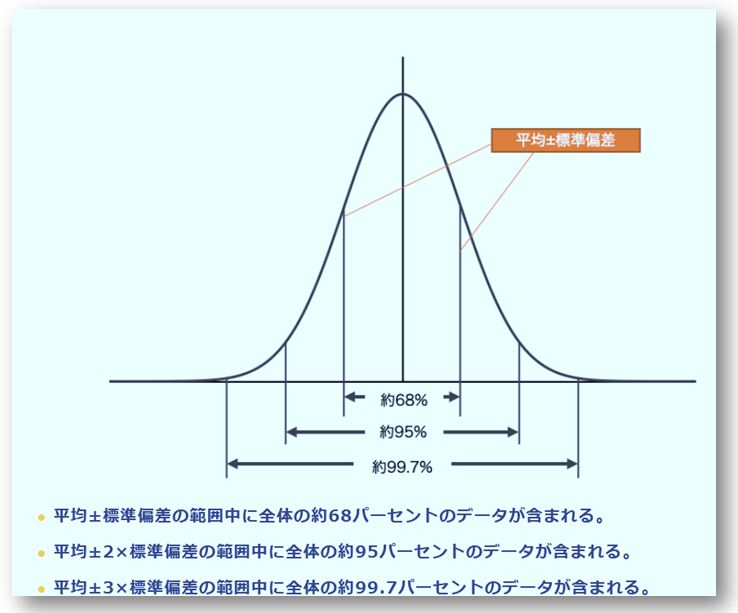
正規分布には、平均や標準偏差の値とは関係なく、次の性質がある。
つまり、標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かります。
この2つ目の性質は、平均や標準偏差の値に関係がなく、この性質を用いたものは、成績を表す偏差値等です。
正規分布を標準化したもの:標準正規分布
平均と分散によって、正規分布はいろいろな形をとることが可能です。
その中でも特に、平均が0で、分散が1のものを”標準正規分布”と呼ばれています。
標準正規分布表の種類
平均が0,標準偏差が1となる正規分布のことを標準正規分布といいます。
そしてその値を一覧にしたものが標準正規分布表です。
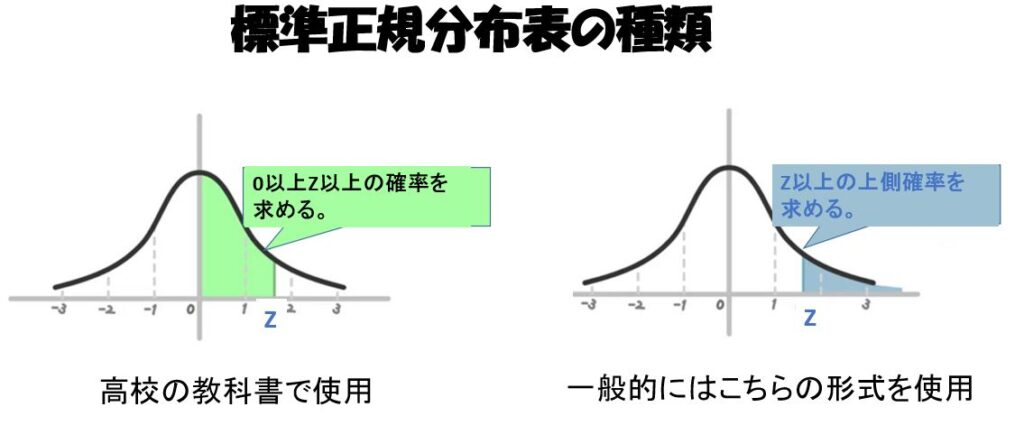
標準正規分布表は2種類あります。
ひとつは高校の教科書に掲載されている上側確率が求められる表と一般的な形式の0〜Zの確率が求められる表の2種類です。
得られる確率は違いますが、最終の求める値は同じです。
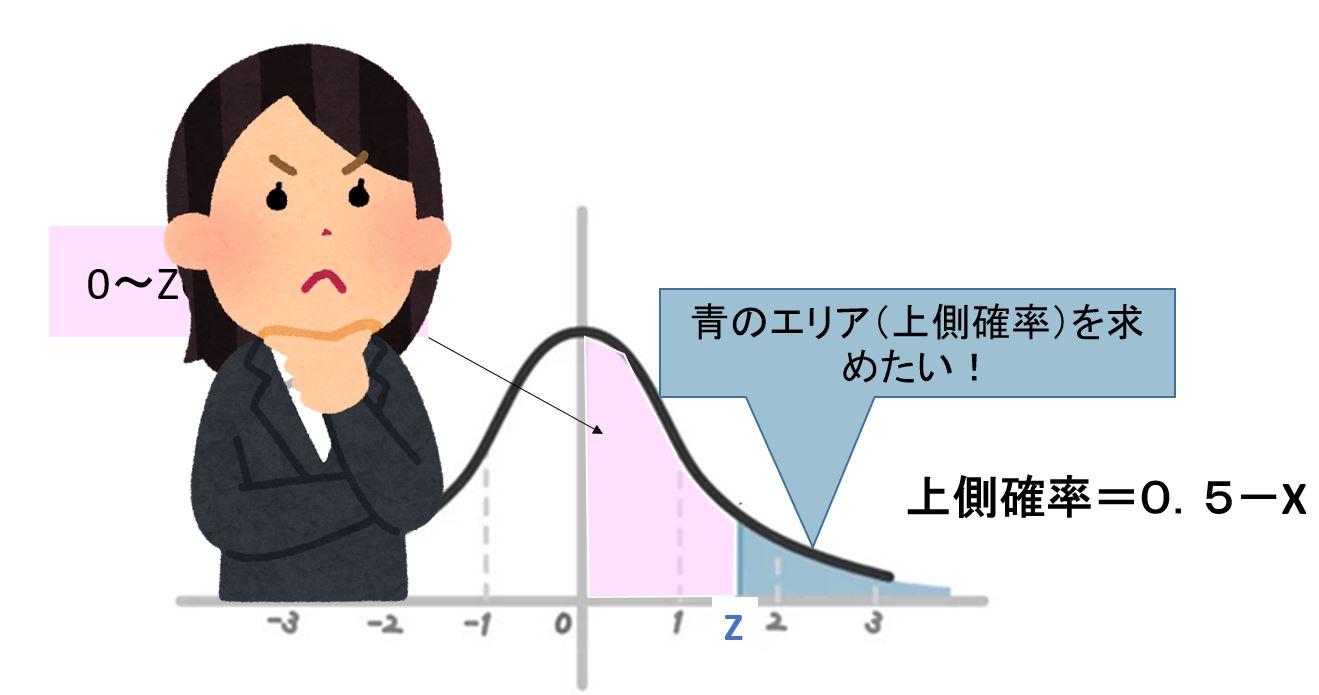
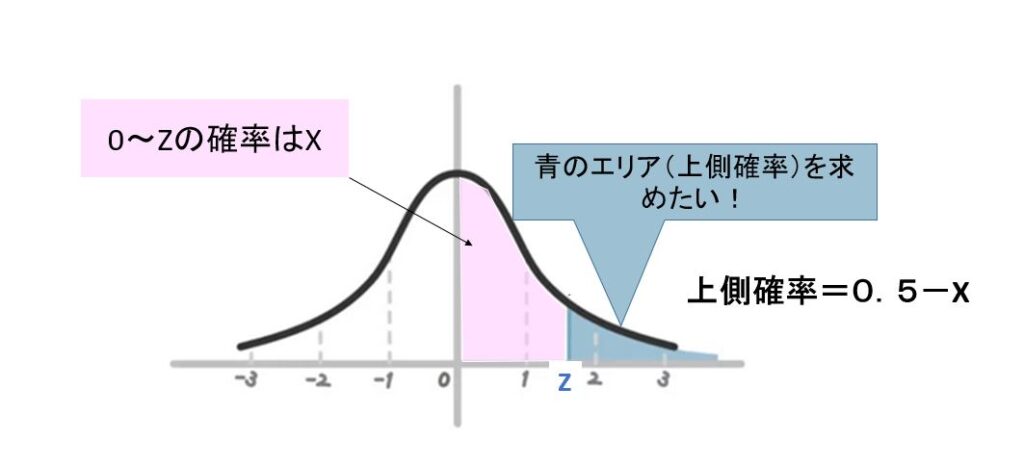
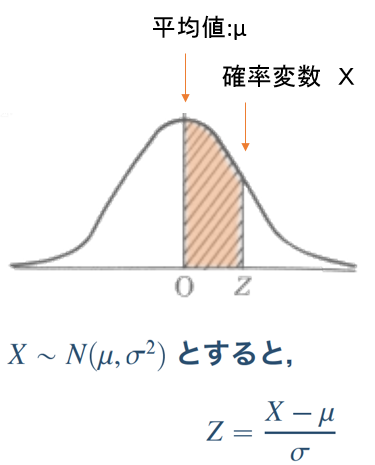
例えば下記の図の場合、標準正規分布表で与えられているのは標準正規分布の右半分なので、この右全体の確率は0.5です(全体の確率は1で、標準正規分布は左右対称だから、確率はちょうど半分)。
よって上側確率を求めたい場合は0~αの確率Xを標準正規分布表で求めて、0.5からXを引けばいい、ということになります。
標準正規分布表 0〜αの確率を求める
高校の教科書や共通テストはこの形式の標準正規分布表。
下記のような図になります。
表の中の値は、全てのの面積を1.0とした場合、Z=0からZまでの面積を示します。
例としてZ=2.00の場合は『0.4772』で、斜線の部分の面積が全体の47.72%です。
よって、ヒストグラムで算出した標準偏差σから変数Xの占有率が簡単に求める事ができます。
標準正規分布表 0〜αの確率を求める
| Z | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | .0000 | .0040 | .0080 | .0120 | .0160 | .0199 | .0239 | .0279 | .0319 | .0359 |
| 0.1 | .0398 | .0438 | .0478 | .0517 | .0557 | .0596 | .0636 | .0675 | .0714 | .0753 |
| 0.2 | .0793 | .0832 | .0871 | .0910 | .0948 | .0987 | .1026 | .1064 | .1103 | .1141 |
| 0.3 | .1179 | .1217 | .1255 | .1293 | .1331 | .1368 | .1406 | .1443 | .1480 | .1517 |
| 0.4 | .1554 | .1591 | .1628 | .1664 | .1700 | .1736 | .1772 | .1808 | .1844 | .1879 |
| 0.5 | .1915 | .1950 | .1985 | .2019 | .2054 | .2088 | .2123 | .2157 | .2190 | .2224 |
| 0.6 | .2257 | .2291 | .2324 | .2357 | .2389 | .2422 | .2454 | .2486 | .2517 | .2549 |
| 0.7 | .2580 | .2611 | .2642 | .2673 | .2704 | .2734 | .2764 | .2794 | .2823 | .2852 |
| 0.8 | .2881 | .2910 | .2939 | .2967 | .2995 | .3023 | .3051 | .3078 | .3106 | .3133 |
| 0.9 | .3159 | .3186 | .3212 | .3238 | .3264 | .3289 | .3315 | .3340 | .3365 | .3389 |
| 1.0 | .3413 | .3438 | .3461 | .3485 | .3508 | .3531 | .3554 | .3577 | .3599 | .3621 |
| 1.1 | .3643 | .3665 | .3686 | .3708 | .3729 | .3749 | .3770 | .3790 | .3810 | .3830 |
| 1.2 | .3849 | .3869 | .3888 | .3907 | .3925 | .3944 | .3962 | .3980 | .3997 | .4015 |
| 1.3 | .4032 | .4049 | .4066 | .4082 | .4099 | .4115 | .4131 | .4147 | .4162 | .4177 |
| 1.4 | .4192 | .4207 | .4222 | .4236 | .4251 | .4265 | .4279 | .4292 | .4306 | .4319 |
| 1.5 | .4332 | .4345 | .4357 | .4370 | .4382 | .4394 | .4406 | .4418 | .4429 | .4441 |
| 1.6 | .4452 | .4463 | .4474 | .4484 | .4495 | .4505 | .4515 | .4525 | .4535 | .4545 |
| 1.7 | .4554 | .4564 | .4573 | .4582 | .4591 | .4599 | .4608 | .4616 | .4625 | .4633 |
| 1.8 | .4641 | .4649 | .4656 | .4664 | .4671 | .4678 | .4686 | .4693 | .4699 | .4706 |
| 1.9 | .4713 | .4719 | .4726 | .4732 | .4738 | .4744 | .4750 | .4756 | .4761 | .4767 |
| 2.0 | .4772 | .4778 | .4783 | .4788 | .4793 | .4798 | .4803 | .4808 | .4812 | .4817 |
| 2.1 | .4821 | .4826 | .4830 | .4834 | .4838 | .4842 | .4846 | .4850 | .4854 | .4857 |
| 2.2 | .4861 | .4864 | .4868 | .4871 | .4875 | .4878 | .4881 | .4884 | .4887 | .4890 |
| 2.3 | .4893 | .4896 | .4898 | .4901 | .4904 | .4906 | .4909 | .4911 | .4913 | .4916 |
| 2.4 | .4918 | .4920 | .4922 | .4925 | .4927 | .4929 | .4931 | .4932 | .4934 | .4936 |
| 2.5 | .4938 | .4940 | .4941 | .4943 | .4945 | .4946 | .4948 | .4949 | .4951 | .4952 |
| 2.6 | .4953 | .4955 | .4956 | .4957 | .4959 | .4960 | .4961 | .4962 | .4963 | .4964 |
| 2.7 | .4965 | .4966 | .4967 | .4968 | .4969 | .4970 | .4971 | .4972 | .4973 | .4974 |
| 2.8 | .4974 | .4975 | .4976 | .4977 | .4977 | .4978 | .4979 | .4979 | .4980 | .4981 |
| 2.9 | .4981 | .4982 | .4982 | .4983 | .4984 | .4984 | .4985 | .4985 | .4986 | .4986 |
| 3.0 | .4987 | .4987 | .4987 | .4988 | .4988 | .4989 | .4989 | .4989 | .4990 | .4990 |
| 3.1 | .4990 | .4991 | .4991 | .4991 | .4992 | .4992 | .4992 | .4992 | .4993 | .4993 |
| 3.2 | .4993 | .4993 | .4994 | .4994 | .4994 | .4994 | .4994 | .4995 | .4995 | .4995 |
| 3.3 | .4995 | .4995 | .4995 | .4996 | .4996 | .4996 | .4996 | .4996 | .4996 | .4997 |
| 3.4 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4998 |
| 3.5 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 |
| 3.6 | .4998 | .4998 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 |
| 3.7 | .4999 | .4999 | .4999 | .4999 | .49991 | .49992 | .49992 | .49992 | .49992 | .49992 |
| 3.8 | .49993 | .49993 | .49993 | .49994 | .49994 | .49994 | .49994 | .49995 | .49995 | .49995 |
| 3.9 | .49995 | .49995 | .49996 | .49996 | .49996 | .49996 | .49996 | .49996 | .49997 | .49997 |
| 4.0 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 |
| 4.1 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 |
| 4.2 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.3 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.4 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.5 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 |
| 4.6 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 |
| 4.7 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.8 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.9 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 |
| 5.0 | .499997 |
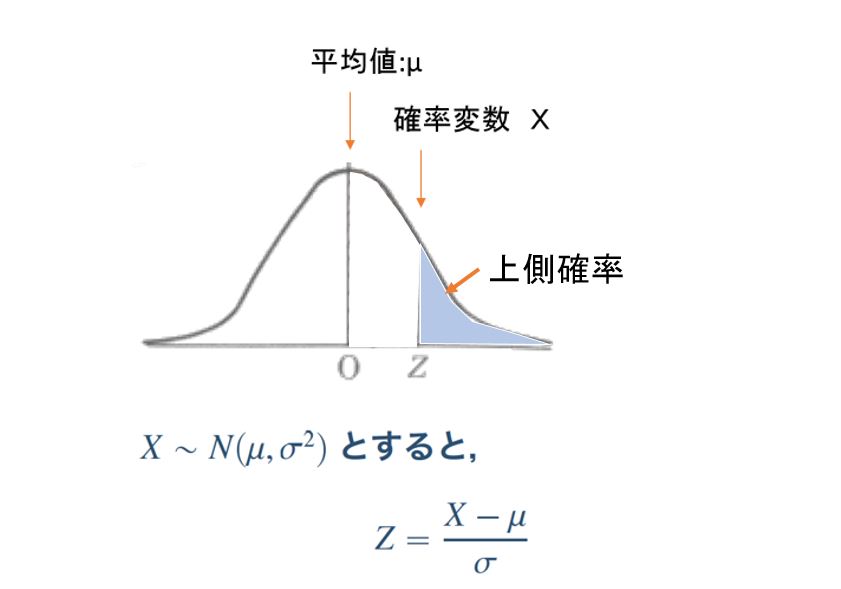
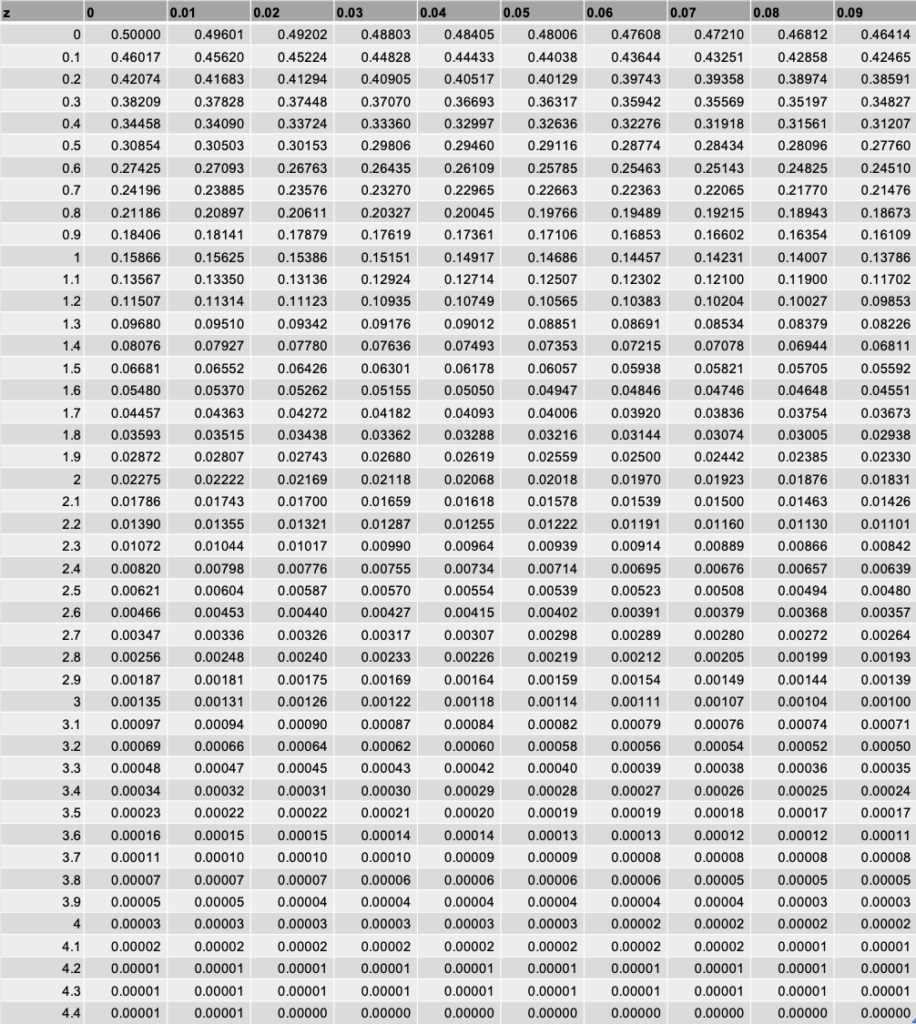
標準正規分布表 上側確率を求める
一般的はこの形式の標準正規分布表が多い。
下記のような図になります。
例としてZ=2.00の場合は『0.002275』で、斜線の部分の面積が全体の2.28%です。
よって、ヒストグラムで算出した標準偏差σから変数Xの占有率が簡単に求める事ができます。
標準正規分布表 上側確率を求める
関連記事:ヒストグラム(度数分布図)作り方【図解】