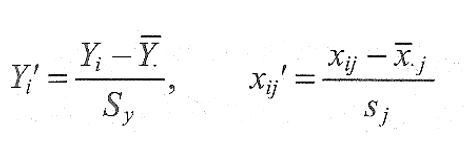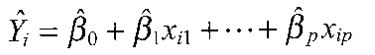- 重回帰分析 multiple regression analysis 【イラスト図解】
重回帰分析 multiple regression analysis 【イラスト図解】
英語:multiple regression analysis 中国語:多元回归分析
重回帰分析とは
変数xi1,xi2,…,xipを固定したとき,確率変数Yiが線形モデル,
Yi=βo+β1+…+β1xi1+βpxip1+ εi
で表される場合の回帰分析.
Yのことを目的変数あるいは反応変数といい, x1,x2,xpのことを説明変数という.
説明変数は連続変量の場合もあれば,質的属性の有無を示すダミー変数の場合もある.
εiは誤差項で通常は暗黙のうちに独立性,不偏性,等分散性を仮定する.
未知母数βoを定数(又は切片),βjをxjに対する偏回帰係数という.
偏回帰係数の推定値は最小二乗法を用いて計算されるが,その値はxjの測定単位を変えると変化するので,それらの相互の比較は意味がない.そこで基準化された変数.
ただし,syは変数Yの標準偏差でありsjは変数Xjの標準偏差に対して重回帰分析を行うこともある。
そのときの偏回帰係数βj’は標準偏回帰係数と呼ばれ,測定単位によらない量となる.
βjの推定値を用いて予測値
が定義される.Yi-平均値Yiを残差と呼び,Σ(Yi-平均値Yi)2を残差平方和(RSS)と呼ぶ.
推定された回帰式とデータとの適合度は,Yiと平均値Yiの相関係数である重相関係数で測られる.
この二乗のことを寄与率と呼ぶが,説明変数間に相関がある場合には,寄与率を(一意的に)各変数に分解することはできない.
重回帰分析においては,説明変数として何を選ぶか,また得られた回帰式がデータの挙動をよく表しているか検証を行うことが本質的である.
前者は変数選択,後者は回帰診断と呼ばれる問題である.
→ロバスト回帰
引用先:クォリティーマネジメント用語辞典 日本規格協会
関連用語:回帰分析

重回帰分析 わかりやすく
重回帰分析は二つ以上の量的な説明変数から、一つの目的変数を予測する手法。 たとえば、接客の質や品数、売場面積などを変数とした小売店の売上などを予測するといった分析です。
つまり、重回帰分析とは、1つの目的変数に対して説明変数が複数存在する回帰分析です。回帰分析のなかでは特に有名な手法であり、複数の要素が1つの要素に対して、それぞれどのように関係しているのかを検証する際に利用されます。例えば、次のような場合です。
例)
・アイスクリームの売上の予測
・一定地域住人の寿命の予測
・顧客満足度の向上に直結する要因の把握
など
いずれの場合も、単回帰分析と比べて要因(説明変数)が複数あることがわかります。例えば、アイスクリームの売上であれば、宣伝広告のほか、店舗の立地や当日の気温といった要因が絡んでくるでしょう。また、顧客満足度の向上に関する要因であれば、価格や品質、サポートなどが考えられます。このように重回帰分析は、ビジネスシーンにおいて利用頻度が高い分析手法の一つです。
重回帰分析の回帰式は「y=β0+β1×1+β2×2……+βkxk+u」で表されます。x1~xkが複数の説明変数を表し、β1~βkは各変数の重みを表しています。
重回帰分析で予測 計算事例
日本経済の消費関数の予測をする。
被説明変数は消費(c)、説明変数は、所得(y)と利子率(r)である。
エクセル等で偏回帰係数で求め、説明変数が確定したら実際に必要な数値を重回帰式に代入し、目的変数(結果)を算出します。
重回帰式:
目的変数=(偏回帰係数×説明変数1)+(偏回帰係数×説明変数2)+(偏回帰係数×説明変数3)+…+定数項
上記の例の場合は推定された回帰式は, 次のようになる。
消費(円)= 0.402×所得(円)- 3032.417×利子(%)+78203.078
重回帰分析と単回帰分析との違い
単回帰分析とは、ひとつの要因から結果を分析・予測する統計的手法です。例えば、広告費と売上の相関関係を求める際に用いる。「広告費を○○円にしたら売上が△△円になった」というような実績データを集め、回帰係数を探す。そしてグラフにして「y=ax+b」といった回帰式を求める。
「y」は目的変数、「x」は説明変数、「a」を回帰係数という。広告費が説明変数、売上が目的変数とするなら、この式のxにいくつか数字を当てはめることで、広告費に対する売上がわかる。
一方、重回帰分析は、複数の説明変数を含む回帰分析です、以下は、広告費・店舗面積・スタッフ数という複数の説明変数と売上という目的変数から成る重回帰分析の例です。
単回帰分析と重回帰分析では、検証する内容や結果が異なるため、どちらの手法を使って回帰分析をするのかが重要となる。
ただし実際のビジネスでは、売上を決める要素はひとつではない。飲食店なら立地や駅からの距離、価格帯、天気などの要素が売上に影響する。結果と複数の要因の因果関係がわかれば将来を予測可能です。
そのため、ビジネスの場面では、2つ以上の要素を用いる重回帰分析のほうが、予測精度を高めるのに適切です。
基本的な構造は変わらないが、重回帰分析は単回帰分析より説明変数が増えるので、式がその分長くなる。
重回帰分析の式は「y=a_1 x_1+a_2 x_2+a_3 x_3+a_4 x_4…a_p x_p+b_0」
分析の流れは、単回帰分析も重回帰分析もほぼ同じです。
重回帰分析をするためには、上記の式で計算したり専用のソフトやExcelを使ったりして求める必要がある。またある程度の理解度がないと結果の解釈やそこから導く予想ができないケースもあるため、注意が必要です。
重回帰分析の利点
重回帰分析の利点としては、主に以下の2点が挙げられる。
現実に即した分析可能
重回帰分析は、複数の変数を同時に考慮できるため、現実の複雑な状況をより正確に反映した分析が可能です。
例えば不動産の価格を予測する際に面積だけでなく立地や築年数、周辺の設備など複数の要因を同時に考慮することで、より現実に即した価格予測が行え、単一の要因だけでは見落としがちな相関関係や影響度を把握できる。
費用対効果の高いマーケティング
重回帰分析を用いることで、マーケティング活動の各要素が売上にどの程度影響しているかを定量的に評価できるようになる。これにより、どのマーケティング活動が最も効果的かを判断し限られた予算をより効果的に配分することが可能となります。
例えばオンライン広告の投資が売上増加に最も寄与していることが分析から明らかになれば、その領域への予算配分を増やすことで、全体のマーケティング効果を最大化できる。
重回帰分析の具体例
・マンション経営
マンション経営では、家賃収入が売上となるため「家賃をいくらにすればよいか」が重要。なぜなら家賃の金額が適正でないと空室リスクを負うからである。
家賃の金額が決まる要因は、駅に近いかどうかや部屋の広さ、設備の充実度合い、築年数などさまざまだ。重回帰分析では、駅に近いかどうかや部屋の広さや設備、築年数などの要因が「説明変数」、家賃の金額が「目的変数」となる。
・飲食店経営
飲食店は、売上高の大小により店舗の経営状態が大きく変わってくるのが特徴です、そのため飲食店の経営をするうえで重要なのが「売上がいくらになるのか」を予測することである。
飲食店では、さまざまな要因が売上の結果に影響を与える。具体的な要因としては、店舗の面積やスタッフ数、メニュー内容、駅からの距離、駐車場の有無などが挙げられる。
重回帰分析では、店舗の面積やスタッフ数、メニュー内容、駅からの距離、駐車場の有無などの要因が「説明変数」、売上高が「目的変数」となる。重回帰分析を活用すれば、新規店の各要因から将来の売上の予測が可能です。
おすすめ関連記事:誰でもわかる!回帰分析の基礎と実践法