製造工場での抜取検査とは
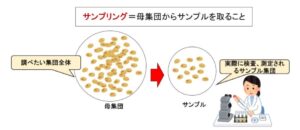
抜取検査は,提出された品物の集まりから一部分のサンプルを抜き取り,それを測定、試験して発見された不良品の数を合格判定個数と比較して合格・不合格の判定を下す検査であり、経済性を考慮した統計的な手法である。
すなわち,抜取検査とは,口ット(品物の集団)から一部のサンプルを抜き取って,そのサンプルについて試験し,結果のデータでロットの合格・不合格を決めるものである。
したがって,抜取検査には,検査稼動が少なくてすむという利点と,一部分しか見ていないため不良品の混入がある,あるいは判定に誤りがあるという欠点がある。
抜取検査の導入にあたってはこれらの利点・欠点をよく吟味しておくことが重要である。
抜取検査を大別すると,計数抜取検査と計量抜取検査とに分けることができる。計数抜取検査とは,サンプルを試験し,サンプルを良品と不良品に分け不良品の数を数えるか,あるいはサンプル中の欠点の数を数えて,あらかじめ定められた判定個数と比較してそのロットの合格・不合格の判定を下す検査である。
計量抜取検査とは,サンプルを試験し,その結果である計量値のデータから平均値,標準偏差を計算して,あらかじめ定められた判定値と比較して,そのロットの合格・不合格の判定を下す検査である。
.
また,検査の形式として,1回抜取形式,2回抜取形式,多回抜取形式などがある。1回抜取形式とは,ロットから指定された大きさのサンプルを1回抜き取ってその試験の結果でそのロットの合格・不合格を判定するものである。
2回抜取形式とは,第1回目として指定された大きさのサンプルを抜き取りその試験の結果からそのロットの合格・不合格あるいは検査続行のいずれかの判定を下す、もし,検査続行という判定が下されたときは,第2回目として指定された大きさのサンプルを抜き取り,その試験結果と第1回目の試験結果の累計の成績によって,合格・不合格の判定を下すことになる。
多回抜取形式とは,毎回定められた大きさのサンプルを試験し,各回までの累計の成績をロットの判定基準と比較して,合格・不合格あるいは検査続行のいずれかを判定し,一定回数までに合格・不合格の判定を下す検査である。
サンプリングについては下記の記事が参考になります。
関連記事:統計調査とサンプリング、標本調査
JISとISO 抜取検査の定義
日本の製造業の抜取検査として、多くの企業で活用されているものがJISZ9015の『抜取検査』です。
このJISZ9015-1の規格は、ISO/DIS2859-1.2 : 1997 の国際規格と一致するように提案されており、JIS規格とISO規格が一致することで、国際的なビジネスにおいて共通に理解ができる検査規格となっています。
JISZ9015の内容には、日本の工業標準として、ISO2859の国際規格にはない説明事項の記載についても、本文中に下線を引いて、わかりやすく区別あります。
JIS Z 9015には、次の3つの抜取検査について記載されています。
*該当項目をクリックすると詳細内容を説明したサイトに移動します。
JIS Z 9015-1 ロットごとの検査に対するAQL指標型抜取検査方式
JIS Z 9015-2 孤立ロットの検査に対するQL指標型抜取検査方式
この中でもシンプルかつ最も多く活用されているのが、「JIS Z 9015-1 ロットごとの検査に対するAQL指標型抜取検査方式」です。
抜取検査が必要な場合 有利な場合
破壊検査
破壊検査項目の場合には全数検査は不可能であるから,無試験ですむ場合以外は抜取検査が必要になる。
抜取検査が有利な場合
ロットの品質がBEQより良いか悪いかはっきりしないときは,抜取検査の方が有利になる場合が多い。
ロットの品質はある程度ばらつくし, BEQ自身もかなりの幅で変わるので,口ットの品質がBQよりも確かに良いとは言い切れない場合が実際には多い。
特に品物が大量だったり金額の大きい場合には,抜取検査の費用は比較的少なくて済むので抜取検査が有利になる場合が多い。
抜取検査の長所
抜取検査は次のような長所をもっているので,その長所を活用するように計画をたてるのが望ましい。
品質についての情報がつかみやすいこと
全数検査だと大量の品物を扱うため,品物が規格からはずれていないかどうかに注意が集中され,仮に測定をしても記録をとることはむしろ少ない。抜取検査では少数のサンプルを調べるため記録がとりやすい。
これは後日工程解析のときに役立つし,また万一苦情が発生した場合には対策の手掛りを与える(工程解析には,多数の計数値データよりも,少数の計量値データの方が役に立つことが多い。
総合的に品質を保証できること
全数検査で検査項目が多い場合には,とかく一部の検査しやすい項目だけ重点的に検査し検査しくい項目は調べ方が不十分になるおそれがあるが,抜取検査では少数のサンプルを調べるので各検査項目を満遍なく調べることが可能となる。
したがって不完全な全数検査よりもかえって品質保証に役立つ場合がある。また,少数のサンプルを調べるので検査ミスも少なくてすむ。
品質改善の刺激を与えること
最終検査で全数を実施していると製造現場の作業者はややもすると検査にたよりすぎて不良品,に対して安易な考え方をいだきがちである。
むしろ抜取検査にして責任所在を明らかにした方が品質水準の向上に役立つ、外注先などからの受入検査の場合にはこういう傾向はさらに顕著である。
【例】 NTTでは主要資材の購入に当たって公社時代の初期には全数検査をしていたにもかかわらず,障害(故障)の発生率が高かった。
1963年に調整型抜取検査を採用し,全数検査はやめたにもかかわらず現在では世界でも最小の障害(故障)発生率に到達している。
抜取検査の条件
抜取検査は,ロットから抜き取ったサンプルの試験結果からロット全体の合格・不合格を決めようとするものであるから抜き取り検査を採用するには次のような条件が必要である。
ロットとして処置がとれること
判定を下す対象が不明確だと混乱のもとなので,検査ロットの範囲を事前に明確に把握する。
合格ロット中にもある程度の不良の混入が許される事
抜取検査では不良率ゼロを保証することはできないのでロットの中に多少の不良品の混入が許されることが必要である。しかし安全に関連する商品とか,宇宙開発など特殊用途の場合などを除けば一般的に多少の不良品の混入は大きな支障にならないことが多い。
ロットを代表するようなサンプルが抜き取れること
サンプルはロットを代表するように通常はランダムサンプリングをする、もし検査ロットが幾つかの副ロットに分かれているときは層別比例サンプリングをする。いずれにしろ,ロットを代表するようなサンプルが抜き取れるようにロットを配置できることが必要である。
規格・標準などが明確であること
抜取検査では1個の品物が良品と判定されるか不良品と判定されるかで,ロット全体の合格・不合格の判定が左右される場合も少なくない。
したがって,誰が判定しても結果が変わらないように,品質判定基準や抜取方式などを明確にしておくことが必要である。
抜取検査の欠点
抜き取り検査の欠点は、「不良品混入のリスク」と「統計学」を学習しなければ使えない事です。
統計の知識が必要
抜き取り検査の精度維持には、適切なサンプリング方法や検査を選択できる統計の知識が必要です。検査するサンプル数を増やす、合格水準を高く設定するなど検査基準を厳しくすれば当然精度は上がりますが、その分検査員の労力は増え、良品にもかかわらず出荷できないロスの量も増加します。
これらの最適なバランスを取るためには、不良品の許容量と検査の工数を統計にもとづいて計算しなければなりません。サンプル数と品質の基準を定める際は、以下の方法があげられます。
| AQL指標型 | 合格の品質上限を定める。基準値を下回らない限り製品は合格する可能性が高い。 |
| LQ指標型 | 製品を不合格にする品質の限界を基準値にする方法。最低限の品質が保証されることを意味する。 |
| スキップロット型 | 一定のロットが基準値を上回る場合、連続するロットを無検査で合格にする方法。 |
不良品流出の危険がある
抜き取り検査はサンプルの状態でロットの品質を判断しますが、実際にすべての製品をチェックするわけではないため、検査対象以外の製品に不良品が含まれる危険をゼロにはできません。
向き採り検査は不良率0%を目指す検査方法ではなく、生産コストの抑制と、不良率の抑制を最大限両立するための検査方法です。
発見率と見逃し率の関係
- 発見率: 抜き取り検査で不良品を発見できる確率です。
- 見逃し率: 抜き取り検査で不良品を見逃してしまう確率です。
この2つの確率は、以下の関係があります。
- 発見率 = 100% – 見逃し率
- 見逃し率 = 100% – 発見率
つまり、発見率が高ければ見逃し率は低くなり、逆に発見率が低ければ見逃し率は高くなります。
抜き取り検査における注意点
- サンプル数: 抜き取るサンプル数が多いほど、不良品を発見できる確率(発見率)は高くなりますが、検査にかかるコストも増えます。
- サンプリング方法: ランダムにサンプルを選ぶなど、適切なサンプリング方法を選ぶことが重要です。
- ロットの不良率: ロット全体の不良率が高いほど、見逃し率が高くなる可能性があります。
- 検査基準: 検査基準が厳しすぎると、良品を不良品と誤判定してしまう可能性があります。
抜き取り検査のメリットとデメリット
| メリット | デメリット |
|---|---|
| コスト削減 | 不良品を見逃してしまう可能性がある |
| 時間短縮 | 全数検査に比べて精度が低い可能性がある |
| 迅速な判断が可能 | 検査結果がロット全体の品質を必ずしも反映しない |
抜取検査 ロットサイズ
ロット 同種類の製品、部品、材料の集まりをロット(Lot)という。ロットは構成品の集められ方、集める目的によって 生産ロット、検査ロット、運搬ロットなどと呼ばれる。
抜き取り検査とはロットを構成する品物の一部をあらかじめ定められた方式で抜き取って試験を行い その結果を判定基準と比較してそのロット全体の合格、不合格を判定する検査方式である。
ロットを構成する品質特性にバラツキがなければロットからサンプルを一個抜き取ってその品質を調べれば ほかの品物の品質も知ることができる。 逆にバラツキが大きい場合はバラツキが少なくなるように同条件で作られた生産ロットで検査ロットを構成 する。
ロット内のバラツキが同じ場合は大きいロットは小さいロットに比べて小さい抜き取り比率で同じ性能の検査を行う ことができる。但しロットが大きくなると生産条件が異なるロットで構成される可能性が高くなるので 抜き取り検査の性能が悪くなる。
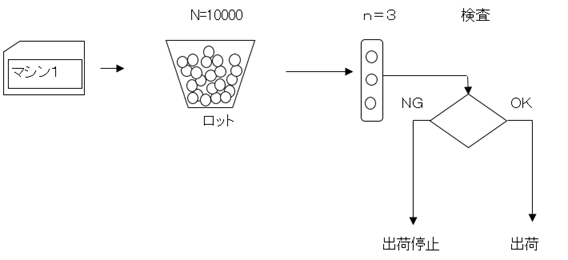
抜き取り検査
ランダム・サンプリング
どのようにサンプルを抜き取るかは検査を行う上で重要なポイントである。
抜き取り検査ではランダム・サンプリングで試料が抜き取られる。 ランダム・サンプリングとはロットを構成する要素が同じ確率で抜き取られるサンプリング方式である。
ランダム・サンプリング方式は確率論を基にデーターを抜き取る為に理論的には正しい方法であるが 現場においてはサンプルをランダムに山積みされた倉庫等から抜き取ることは容易でない。
さらに具合が悪いことには得られたサンプルがランダムにとられたかどうかを後から証明するのは 不可能なことである。その為これらの問題を解決するために色々な工夫が行われている。
解決策1:
サンプリングを対象物の移動中に行う。 例:倉庫に製品が運搬されている時にサンプリングを行う。
解決策2:
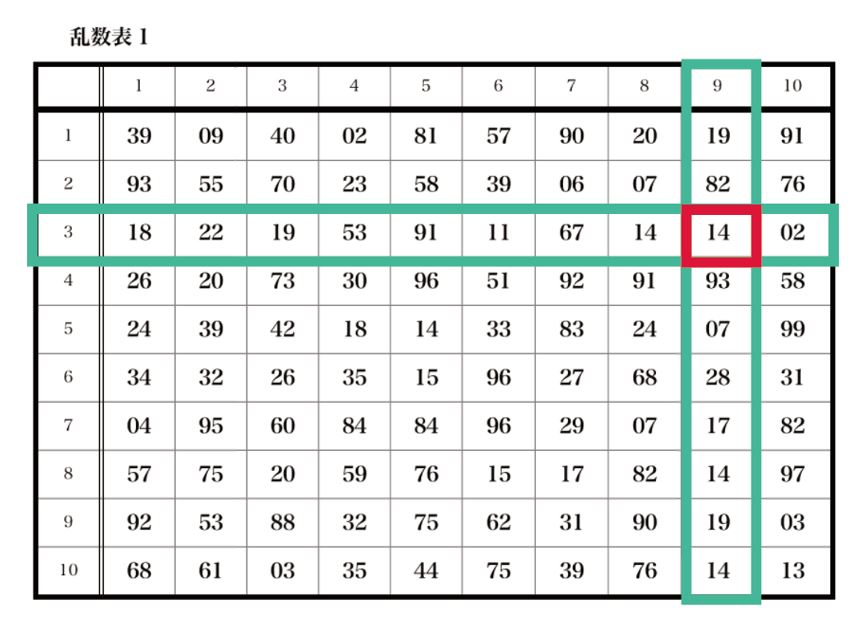
乱数表を使用する
関連記事:統計調査とサンプリング、標本調査~乱数表
製造工場 抜取検査の種類
抜取検査の種類 には下記の種類がある。
不良個数による抜き取り検査・・・計数抜き取り検査
欠点数による抜き取り検査・・・計数抜き取り検査
計量値による抜き取り検査 ・・・計量抜き取り検査
不良個数による抜取検査
検査単位の品質を良品か不良品かに分けて表す場合の抜き取り検査でロットの品質を不良率で表す。
【例1】:
ネジ抜き取り検査においてロットの大きさ700個に対してサンプルとして100個抜き取りこの中の不良品が2個以下ならば合格とし3個以上ならば不合格とする。
欠点数による抜取検査
検査単位の品質をそれがもつ欠点によって表す場合の抜き取り検査でロットの品質を100単位当たりの欠点数によって表すのが特長である。
【例2】:
あるシャツの抜き取り検査においてロットの大きさ300枚のロットからサンプルとして20枚を抜き取りこの中の欠点数合計が5以下ならばロットを合格とし6以下ならば不合格とする。
計量値による抜取検査
検査単位の品質をその測定値によって表す場合の抜き取り検査でロットの品質を平均値又は不良率で表す。
【例3】:
ある製品の単位重量が50.0g以上と定められている場合、サンプルとして10個を抜き取りその平均値が50.35g以上ならばロット合格として50.35g未満ならば不合格とする
抜取検査の型
抜取検査は一般に次の四つの型に分類される。
(a)規準型 (b)選別型 (c)調整型 (d) 連続生産型
規準型抜取検査
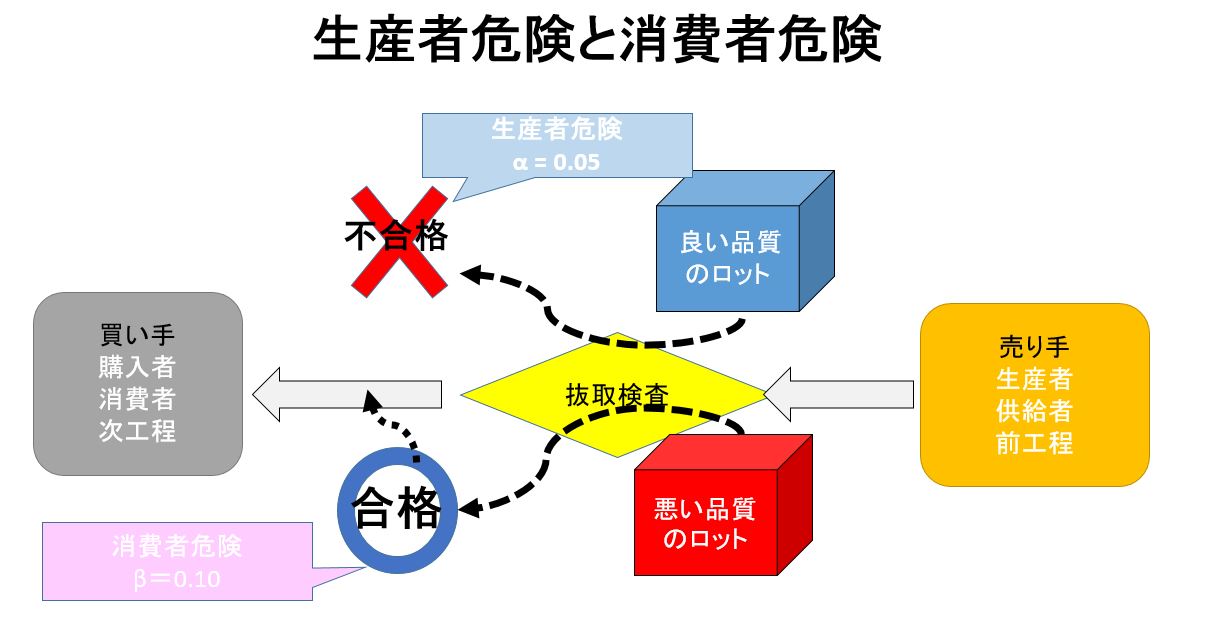
売り手に対する保護と買手に対する保護との二つを規定して売り手の要求と買手の要求を満足するように作られている。
売り手に対する保護は良い品質のロットが検査で不合格となる確率α(生産者危険という)を一定の小さい値に決めることによって与えている。
買手に対する保護は悪い品質のロットが合格となる確率β(消費者危険)を一定の小さな値にして買い手の保護を保証する。
通常はα=0.05であり 100回のうち5回が良い品質のロットが検査で不合格となる。
又、β=0.10であり100回のうち10回が悪い品質のロットが検査で合格となる。
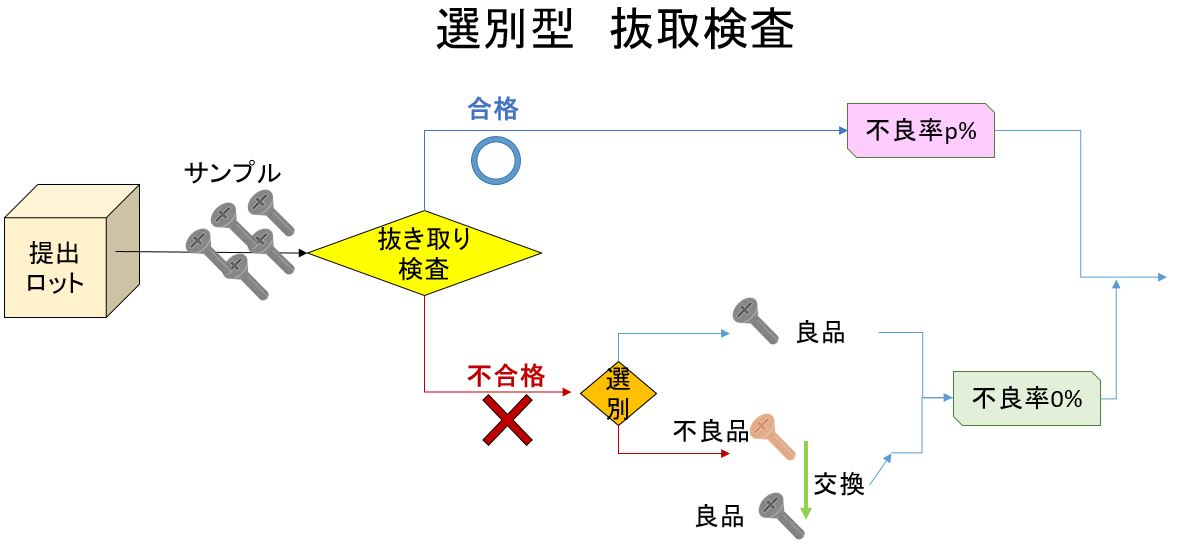
選別型抜取検査
抜き取り検査で合格となったものはそのまま受け入れるが不合格となったものは全数選別するタイプの抜き取り検査 したがって全数検査ができない破壊検査には適用できない。
この型の抜取検査では,全数選別されたロットは不良品が除かれてしまうから,全数選別を受けずに合格したロットの不良率と比べると小さくなる。
検査後の平均の不良率をAOQ:average outgoing quality(平均出検品質)と呼ぶ。
例としてN=2000、n=100 ,c=2の場合のAOQをロットの不良率を変化させて計算し、結果を図で曲線で表したのが下図である。
横軸にロットの不良率p、縦軸にAOQを取って計算結果をプロッタした曲線をAOQ曲線と呼ぶ。
この曲線を見て分かるように,ロットの不良率がゼロから増加するにつれてAOQの値も増えるが,ある不良率(この場合にはp=2%付近)のところでAOQの値が最大となり,それからはロットの不良率が増加するにつれAOQの値は小さくなってだんだんゼロに近づき,ロットの不良率が100%でAOQの値は完全にゼロとなる。
したがって不合格ロットは全数選別するという条件のもとに,ある一定の抜取方式で検査を行うと,検査に提出されてくるロットの不良率がどのような値であっても検査後の平均出検品質AOQはある一定値を越えない、この一定値をAOQL:average outgoing quality limit(平均出検品質限界)という。
このように選別型抜き取り検査ではどんな不良率のロットが提出されても検査を通過した品物の品質は平均してAOQLの値より悪くないという保証を与えることができる。
なお,全数選別を受ける場合と全数選別を受けずに通過する場合との検査量平均を考え,これを工程平均不良率の下において最小にするという条件をも考慮して抜取検査方式を決めるのが普通である。
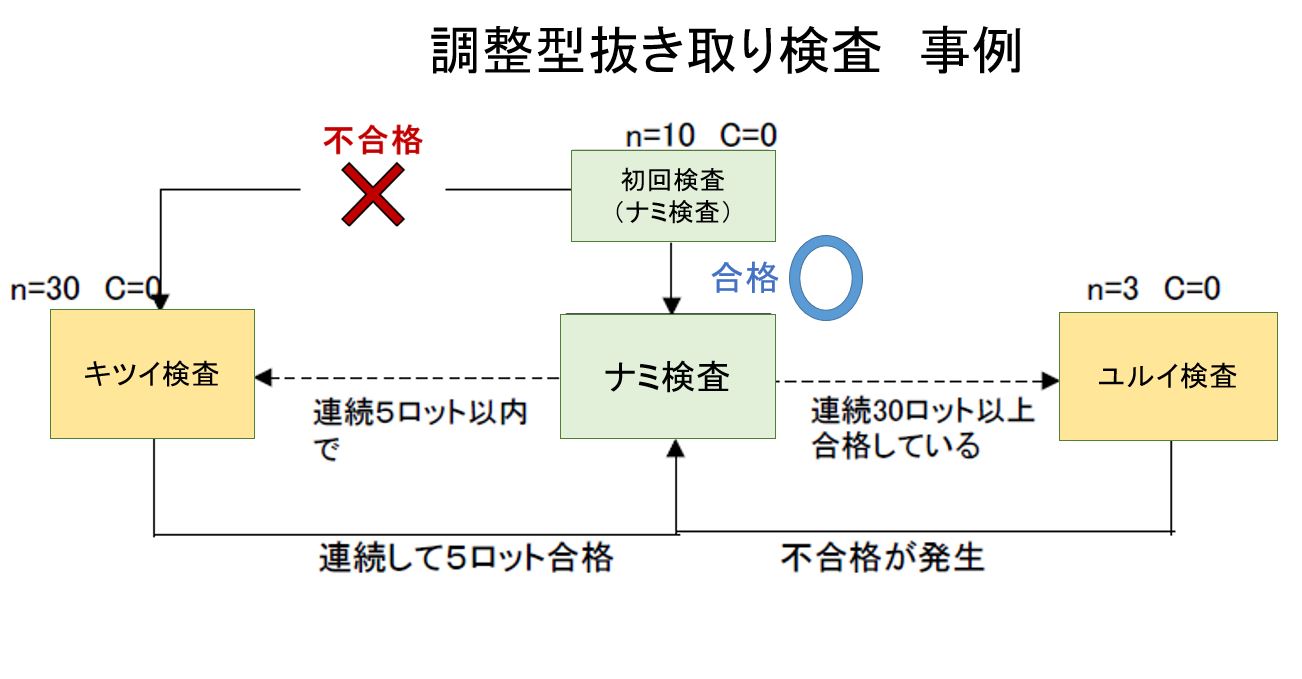
調整型抜取検査
量産製品で同じ供給者によって製品の受け渡しが継続的に行われる場合にはこれまでの検査の結果の情報を 利用することによって合理的な検査を行うことができる。 すなわちこれまでの検査成績がよい供給者について検査を緩和し(ユルイ検査)、成績の悪い供給者については厳しい検査(キツイ検査)を行うのである。
このような調整する抜き取り方式を調整型抜き取り検査という。 多くの購入検査においてこの検査方式が採用されている。 調整型抜き取り検査においてはまず合格品質水準 (AQL: Acceptable Quality Limit)を設定する。
AQLは供給側と受け入れ側で決めた価格に対して受け入れ検査時に承認した不良率である。
高い原材料を使用すれば不良率が低下するが逆に価格が高くなる場合は買手にとって必ずしも 有利とはならない。
多少、不良があっても選別検査等で品質を確保できる場合は廉価な原材料でよい場合もあるのでコストとのバランスを 考慮してAQLを決める。
追加
調整型抜取検査は,検査にロットが継続して提出される場合に,その品質に応じて検査のきびしさを変えるところから,この名称がついている。 このような特徴から,従来は購入検査に使用する規格として長い間、用いられてきた。
この規格は, MIL-STD-105 (アメリカ軍用規格)として制定されたものを母体として, 1974年にISO 2859 として制定され,その後改訂され改善が加えられている。
これに対応するJIS Z 9015が1971年に制定された. 1999年には改正されて, JIS Z 9015-1としてISO 2859-1に一致した規格になっている。
このような改正の中で,この規格は抜取検査の中核を占める規格になり,世界的にも最もよく用いられるものとなり,購入検査に限らず,工程内検査,最終検査にも広く用いられている。
なお,規格の正式名称は調整型という用語は用いず, JIS Z 9015-1(計数値検査に対する抜取検査手順一第1部:ロットごとの検査に対するAQL指標型抜取検査方式)である.
連続生産型抜取検査
連続して生産されている状態のままで適用する検査型であり具体的には最初一個、調べその後 良品が一定個数続いたら一定個数おきに抜き取り検査し不良がでると再び一個ずつ検査に戻る方式である。
抜取検査とOC曲線
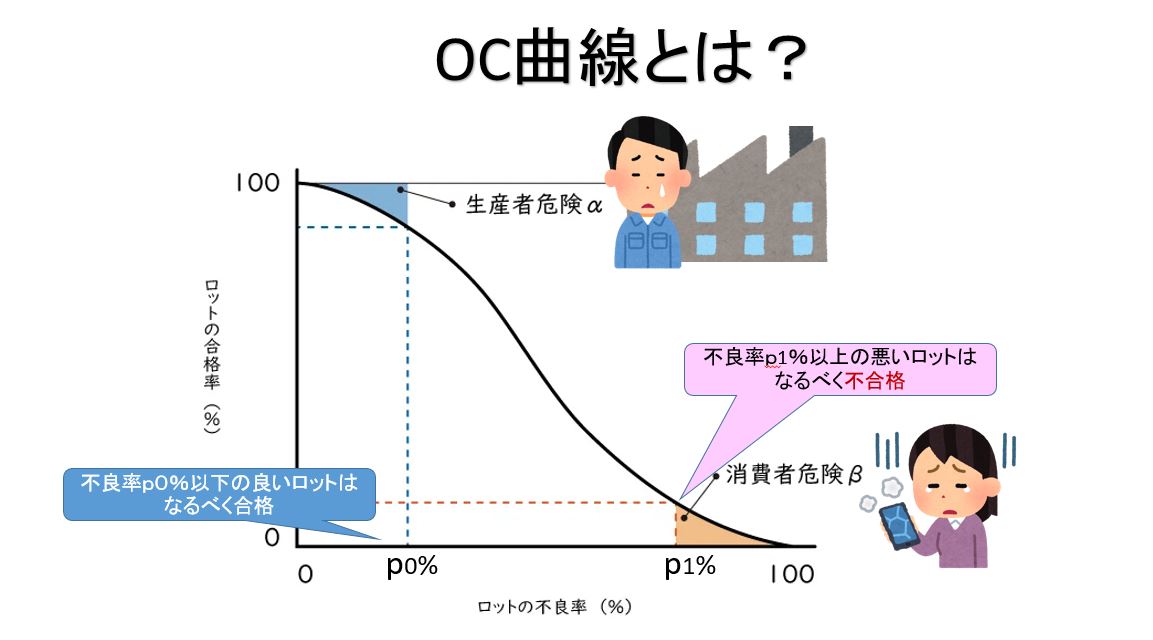
計数抜き取り検査では不良率p0%以下の良いロットはなるべく合格としp1以上の悪いロットはなるべく不合格となるようにしたい。
下図のα(=1-P(p0))は、本当はロットの不良率はp0よりも小さく合格すべきなのに、不合格だと判定される確率になります。αを第1種の誤りといい、これが大きいと生産者が不利になるので生産者危険ともいいます。また、あわてて不合格にしてしまうことから「あわて者の危険」ともいいます。
又、下図のβ(=P(p1))は、p=p1のときに、このロットが合格する確率がβだということです。すなわち、本当はロットの不良率はp1よりも大きいのに、合格にしてしまうことです。
βを第2種の誤りといい、これが大きいと消費者が不利になるので消費者危険ともいいます。また、誤りに気付かないで合格にすることなので「ぼんやり者の危険」ともいいます。
そのためロットから大きさnのサンプルを抜き取りその中の不良品数の数がc個以下ならばロットを 合格、c個を超える場合は不合格とする方式を取る。これを抜き取り検査方式といい(n、c)と略記する。
例として1%以下の不良率は合格とし4%以上の不良率のロットは不合格としたいものとする。 二項分布を使用してサンプルnにて抜き取った場合のX個不良がでる確率は下記の式から求めることができる。
$$P(x)=\frac{n!}{x!(n-X)!}px(1-p)n-x$$
(x=0,1,2,3,4・・・n)
n=10,X=0 の場合は大きさ 10のサンプル中に1個も不良がでない確率は
$$P(0)=(1-p)10$$
となり計算結果は下記のようになる。
大きさ 10のサンプル中に不良品が発生しない確率
| p(%) | P(0) | p(%) | P(0) |
| 0 | 1.000 | 10 | 0.349 |
| 1 | 0.904 | 15 | 0.197 |
| 2 | 0.817 | 20 | 0.107 |
| 3 | 0.737 | 30 | 0.028 |
| 4 | 0.665 | 40 | 0.006 |
| 5 | 0.599 |
表によれば,不良率が1%の場合には, x=0となる確率は0.904である。
すなわち所望の良いロットが合格となる確率は確かに大きいが,誤って不合格としてしまうことも10回に1回はある。次に不良率が4%の悪いロットであっても合格する確率は0.665と大きい。さらに不良率が10%のロットでも平均して100回中35回はサンプル内に不良品が1個も現れず合格としてそのロットを受け入れてしまうことになる。
すなわち,適当にサンプルを抜き取ってみて不良品が少ないから合格にしようという方法では不良率の大きな悪いロットでも誤って合格としてしまったり,良いロットを不合格としてしまう確率が大きくなり得る、これでは出荷時における十分な品質の保証もできないし,購入時にも安心してロットを受け入れることもできない。
あるいは,良いロットをたびたび不合格としていては選別費用がかさんだり,そのロットを用いた生産の計画が狂うてしまうこともある。そこでサンプルのばらつきを考慮した検査方式の動作特性を知ることが,妥当な抜取検査を実施するうえで重要となる。
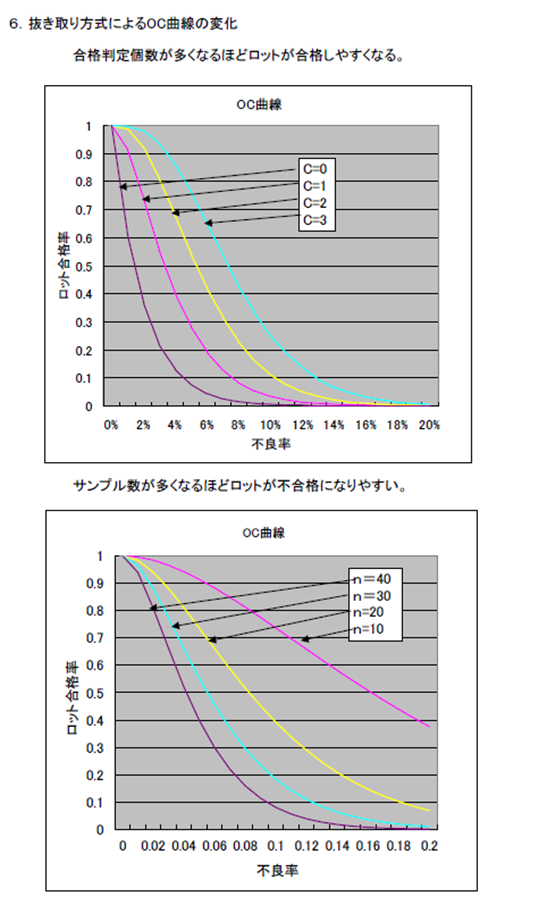
例えば上に述べたような“10個をランダムに抜き取り,その中に不良品が1個もなければロットを合格とする”という抜取方式の特性を表すと下図 2. 2. 1 のようになる。
このように横軸にロットの不良率pを,縦軸に合格の確率((L(p)と書く)をとった図をOC曲線(operating characteristic curve)という。
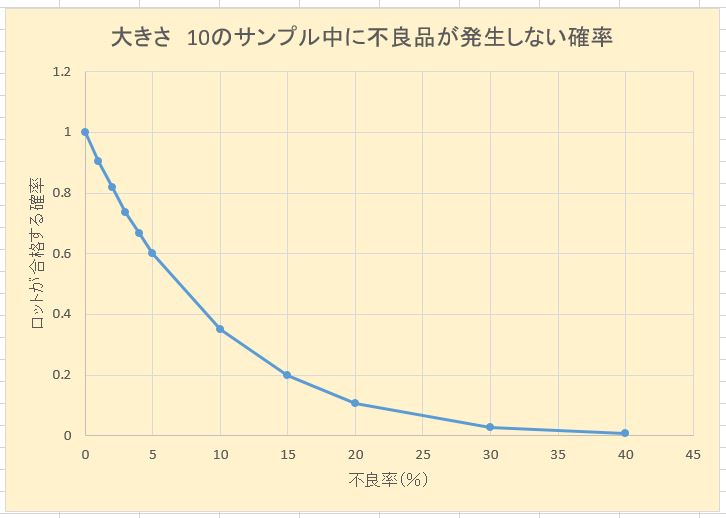
OC曲線は一つの抜取方式が決まれば,これに対して一意的に決まってくるものである。したがって,OC曲線を書いてそれを調べ,その抜取方式では
①どの程度の不良率のロットがどれぐらいの割合で合格になるか?
②ロットをある割合で合格させるためにはロットの不良率をどの程度にしなければならないか?
などということを知っておくことが大切である。
一般的なOC曲線の形状に,生産者危険((Xという記号で表す)と消費者危険 (βという記号で表す)との関係を示したのが下図である。
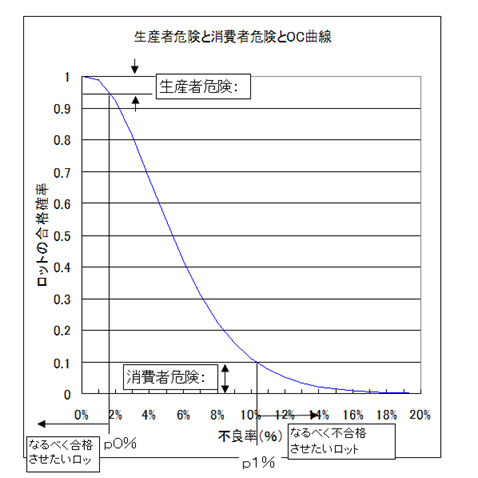
検査曲線と消費者危険、生産者危険
計数抜取検査の定義
抜き取り方式(n、c)が与えられた場合に不良率p%のロットがその抜き取り方式で合格する確率は 次のようにして求めることができる。 大きさnのサンプル中にx個の不良品が出現する確率をP(x)とする。
ロットが合格するといういうことは サンプル中の不良個数がc個以下すなわちx≦cを意味する。そこでロットが合格する確率は サンプル中のに不良品が0,1、(c-1)、c個発生する確率P(0)、P(1)、P(2)、P(3)、P(c)を求め これらをすべて加えたものが「合格の確率L(P)となり次式のようになる。
$$L(p)=P(0)+P(1)+・・・P(c)=\sum_{x=0}^{c} P(x)$$
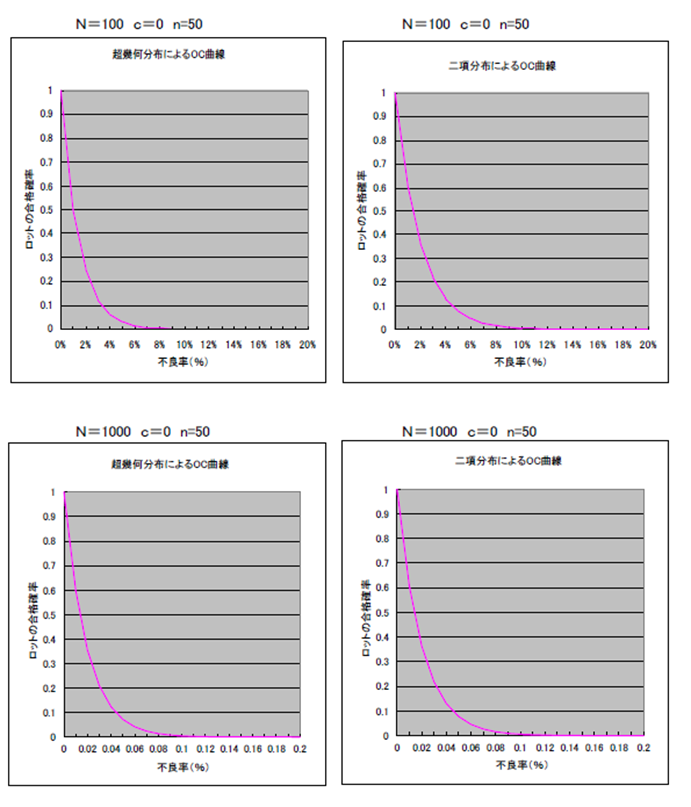
次にP(x)を求める場合、計数抜き取り検査の場合は超幾何分布を用いて下記の式で計算を行う。
$$P(x)=P(x,n|p,N)$$
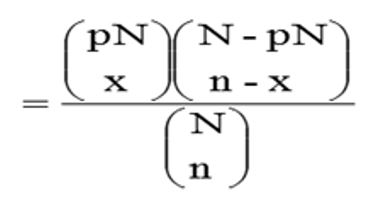 但しNが大きくなると超幾何分布と二項分布は近似するのでN/n>10の場合には計算が容易な二項分布で計算しても実務上問題ない。
但しNが大きくなると超幾何分布と二項分布は近似するのでN/n>10の場合には計算が容易な二項分布で計算しても実務上問題ない。
抜き取り検査とOC曲線1
抜き取り検査とOC曲線2






















コメント
例として上がっているところが間違っています。
「なみ検査の1回抜取方式(主抜取表)を選択して、サンプル文字Gで、AQL=0.25%を選択した場合、下の表の↓の下の抜き取り方式を採用します。
この場合はn=32 Ac=0 Rc=1です。」
とありますが、矢印に従いサンプルサイズも変わりますので、n=50の間違いですね。
表の注記に「矢印の下の最初の抜き取り方式を使用する。」とあり、「抜き取り方式」とは「サンプルサイズ」「Ac」「Re」が該当します。
Take様
連絡ありがとうございます。ご指摘どうりです。即時 修正しました。
抜取検査における「矢印」の解釈について確認させていただきたくご連絡いたしました。
私の理解としては、矢印の意味は 判定基準(Ac/Re)の選択に関わる ものであり、サンプルサイズ(抜取数)自体は変わらないものと考えておりました。
ところが一部の資料を確認すると、矢印の指示に従って サンプルサイズそのものが変化する ような解釈がされているように見受けられます。
そこで質問です。
矢印は 判定基準のみを変更する 指示なのか
あるいは サンプルサイズ(抜取数)も変更対象になるのか
この点について、JISもしくは関連規格の公式な説明や根拠となる文書がありましたら、ご教示いただけますと幸いです。
よろしくお願いいたします。