- 統計学 statistics 【イラスト図解】
統計学 statistics 【イラスト図解】
英語:statistics 中国語:统计学
ある集団や現象の牲院を明らかにするために,標本調査法や行政資料に基づいて作成された数値的情報を統計といい、統計を対象とする科学を統計学あるいは統計科学といい,そこから,数理統計学,統計的推測論,統計的方法などが発達した。
私たちの周りには膨大なデータがあふれていますが、並んだ数字を見ているだけでは意味がありません。 統計学では、それらの膨大なデータを分析し、データの特徴や規則性・不規則性、データ同士の関連性を割り出します。
統計学の分類
統計学は大きく分けて記述統計学、推測統計学とベイズ統計学の3つに分けることができます。
記述統計学 descriptive statistics
記述統計学とは集めたデータから表やグラフを作ったり、平均や傾向を調べることによってデータの特徴を把握するという方法です。
調査を行う際には、多くのデータを集めますが、そのデータを表計算ソフトに入力してみても、その特徴は一目で分かりません。
したがって、データがどういうことを表しているかを知るために、表やグラフを作るという方法が用いられます。
事例を上げます、まずはデーターを集めて表にします。
次に相対度数表を作成します、データーの出現頻度を求めます。
|
10
|
0.10
|
|
|
20
|
0.20
|
|
|
40
|
0.40
|
|
|
20
|
0.20
|
|
|
10
|
0.10
|
|
|
100
|
1 |
相対度数はそれぞれの階級の度数の全体に対する割合です、よってすべてを合計すると1になります。
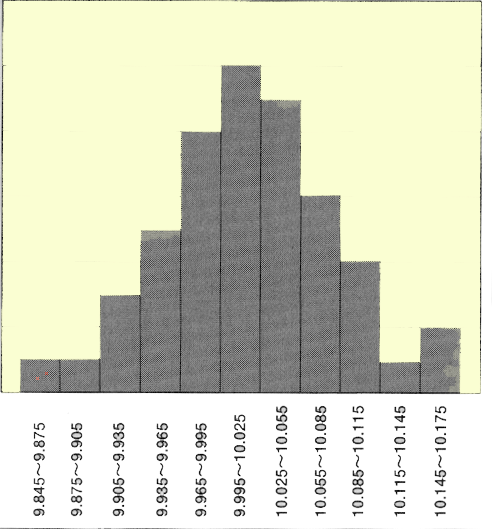
この度数分布表をヒストグラムにすると、下のようになります。
横軸に測定値を、縦軸にデータ数を取ります。区間ごとのデータ数を棒グラフで表わします。これがヒストグラムです。
関連記事:記述統計学
推測統計学 inferential statistics
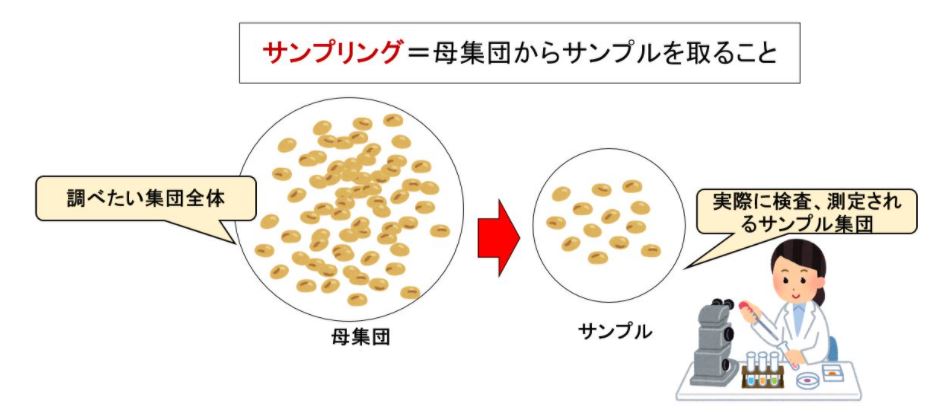
推測統計学とは、母集団から一部のデータ(標本)をサンプリングしてそのデータの特徴から母集団の特性を推測するという方法です。
推測統計学では、推定と検定にさらに分類することができます。
推定とは、平均値等を予測をすることであり、検定とは母集団について立てた仮説が正しいかどうかを統計学的に検証することをいいます。
事例として日本人の平均体重を求めます。
平均を求めるには、全数調査をするのが一番正確な方法となりますが、日本人の平均体重となると、全数調査をするのは困難です。
したがって、標本となるデータを抜き出して、その平均を求め、日本人の平均体重を推測する、というのが妥当な方法となります。
これが推測統計学です。
そして、推定は、抜き出したデータから日本人の平均体重を推測するということであり、検定は、日本人の平均身長は60kgと言われているけれど、抜き出したデータの平均が58kgであった、という時に抜き出したデータが妥当であったかどうかを検証することです。
推定には、「点推定」と「区間推定」という2つの方法があります。
点推定は「1つの値」を抜き出して推定するのに対し、区間推定は「一定の区間の値」を抜き出して推定する方法です。
推測統計学を利用している例としては他に「テレビ番組の視聴率」や「平均年収」「「選挙の出口調査」などがあります。
関連記事:推測統計学
ベイズ統計学 Bayesian statistics
ベイズ統計学とは、ベイズの定理を用いた統計学です。
ベイズの定理とは、18世紀にベイズによって発見され、ラプラスによって確立されたもの。
ベイズの定理の式は以下のようになります。
\begin{eqnarray} P(H|D) = \dfrac {P(H)P(D|H)} {P(D)} \end{eqnarray}
H:仮説 D:データ
事前確率 P(H):事前にデータ D が何もない状態で、仮説 H が正しい確率
尤度 P(D|H):仮説 H が正しいとした時の、データ D の尤もらしさ
周辺尤度 P(D):仮説 H の真偽を問わず、データ D を観察する可能性
事後確率 P(H|D):データ D を踏まえて、仮説 H が正しい確率
ベイズ統計学は標本を必要としない考え方であり、標本を必要とする推測統計学や記述統計学と大きく異なります。
また、推測統計学や記述統計学は母数が不変でデータが変わるという考えるものであるのに対し、ベイズ統計学は母数は変わり、データが不変であるという考えです。
ベイズの定理では「原因」→「結果」ではなく、「結果」→「原因」という「原因の確率」「逆確率」を求めるものであり、迷惑メールの判別やアプリケーションの開発、検索エンジンや機械学習に用いられています。
一般的な統計的推定とベイズ推定の違い
あなたが新型コロナウイルス抗原検査キットで新型コロナが陽性の時、実際に新型コロナに罹患している確率(%)は? 条件は下記の通り。
・日本での新型コロナの羅漢率は4%
・新型コロナの罹患者を新型コロナウイルス抗原検査キットで検査すると80%の確率で陽性になる。
・健康な人を新型コロナウイルス抗原検査キットで検査すると95%の確率で陰性になる。
ベイズの定理では、”原因→結果”ではなく、”結果→原因”という、時間の流れが逆の、「原因の確率」を論じます。
このような事後確率を「逆確率」といいます。(今回の問題では、新型コロナが原因で、新型コロナウイルス抗原検査キットが結果です。)
ベイズの定理の数式に当てはめて計算すると
= {0.80×0.04}/{0.80×0.04+ 0.05×0.96}
= 0.4≒ 40(%)
健康な人が新型コロナウイルス抗原検査キットで陽性反応が出た場合、本当に新型コロナに罹患している確率は約40%です、逆に言えば約60%方は感染してなく誤診です。
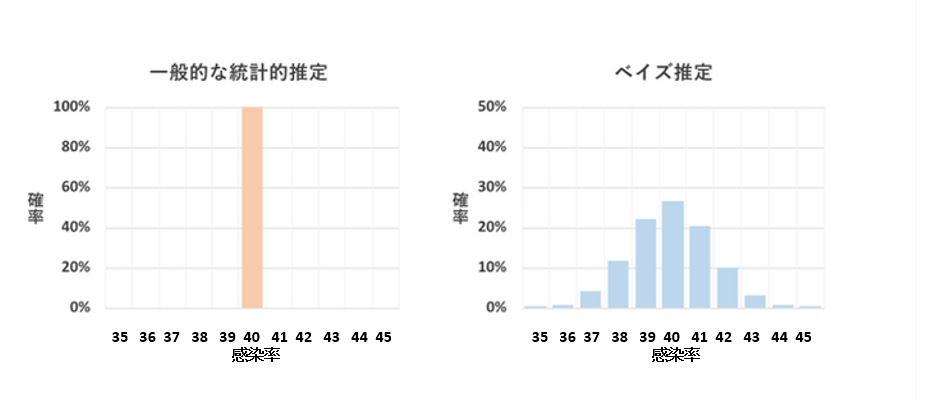
一般的な統計的推定である回帰分析では「感染率は40%」といった一意の値が結果となります。
しかし、「手元にある一部のデータから推測するので、感染率は平均的に40%です。
回帰分析自体は手軽に扱えて便利な分析手法ですがデータ全体が見えていないにも関わらず、「感染率は40%」と一義的に決めつけることができるでしょうか?
この点に対し、ベイズ推定では「感染率は40%の可能性が高いが、39%の可能性も少なからずあり、41の可能性もある」といった考え方をします、ベイズ推定の結果は一意の値ではなく、影響力の確率分布となります。
統計学とデータサイエンス、データリテラシーの違いは?
統計学は、定量的なデータを収集して解釈しようとする数学ベースの分野です。 対照的にデータサイエンスは科学的な方法、プロセス、およびシステムを使用して、分野を横断してさまざまな形式のデータから知識を抽出し、ビジネスにとって意味のある本質を抽出するためのデータの研究です。
一方、データリテラシー(data literacy)とは、データ(data)の読み書き能力、活用する能力の事、広く言えば、データを扱う能力全般を言います。( literacy:読み書き能力)
データリテラシー、データサイエンス どちらも定義が定まっていませんが簡単に説明するとデータサイエンスはデータを収集し処理するための手法、そのための数学的知識、コンピューターソフトウェアの使いかた、ビジネス活用などからなります。
それに対してデータリテラシーは統計処理する以前のデータに対する扱い方に重きを置きます、データについての常識に近いものです。
データリテラシーは、データサイエンスの一部を支えており、統計解析スキル(ビックデータを統計処理し、視覚化する)に該当します。
関連記事:データリテラシーとデータサイエンスの違い
統計学 検定、資格
統計に関する公的資格には統計検定1級、統計検定準1級、統計検定2級、統計検定3級、統計検定4級、統計調査士、専門統計調査士、国際資格の8つである。
関連サイト:統計検定
2021年4月にデータサイエンティスト協会が「データサイエンティスト検定™(DS検定™)」を開始しました。こちらは民間資格になります。
検定は4つのレベルが設けられており、現在は一番簡単なレベルのみの提供となっています。データサイエンティストに必要な知識が幅広く出題されます。
関連サイト:データサイエンティスト検定
統計学の活用分野
基礎統計学 Basic Statistics
基礎統計学とは、データの収集・整理の方法や、基本的なデータ解析方法、統計学の考え方などを対象とした学問です。主に、大学で初めて統計学を学ぶ人を対象にしています。
大学の統計学の授業では、講義を聴くだけでなく、Excelなどの表計算ソフトや統計解析ソフトを使って実践形式で学ぶ場面も多くあります。高校の数学で習う微分・積分の知識が必須。
社会統計学 social statistics
社会統計学とは、社会調査を行うときに利用する統計学のことです。社会調査とは、社会や集団の意識・実態を調査すること。代表的なものとして、国勢調査や世論調査があります。
社会調査では、調査したい対象の母数が多いので全員に調査できない場合に、統計学を活用した「標本調査」でサンプリングし、データを収集・分析します。標本調査の手法はアンケートが一般的ですが、ほかにもSNSなどで公開されている情報を集めたり、現地に出向いてデータを収集したりすることもあります。
心理統計学 psychological statistics
心理学の研究で活用されるのが、心理統計学です。人の心は目で見ることはできず、つかみどころのないもの。心理統計学を活用することで、人の心を数値に置き換えて科学的に分析します。
例えば、企業のブランド力を数値化して把握するために、アンケートを実施して分析するといった活用法があります。
統計的品質管理 statistical quality control
統計的方法を活用して,品質や工程の改善を行うことを主体とする品質管理 SQCと称されることもある。
統計的方法 statistical method
現象をばらつきの伴う事象とみて,統計手法を使いながら,データを集めて分析したり研究する方法.その基本を,統計的考え方(statistical thinking)ということもある,統計手法には,QC七つ道具に含まれる手法から,回帰分析などの多変量解析法,標本調査法,実験計画法などがあり,品質管理における統計的方法を統計的品質管理(SQC)という。
統計学を活かせる職業
統計学が活かせる職業ついての解説です、就職、求人情報の参考にしてみてください。
科学者、研究者、専門家
科学者、研究者、専門家は、企業や大学、研究所などで、まだ発見されていない知識や技術を研究します。どのような分野の研究でも共通するのは、仮説を立てて調査・実験し、その結果を分析すること。
その過程で、統計学を使ってデータを正確に扱うことが求められます。統計学の知識があれば、データから結論を導くまでのエラーを防ぎ、正確な分析が可能です。
リサーチャー、市場調査員
リサーチャーとは市場調査をする人のことです。市場調査とは、新しい商品やサービスを企画するときや販売した後に、お客が求めているものやライバル会社の動きなどを調査することをいいます。調査のために試供品を提供してアンケートを実施したり、X(旧Twitter)やInstagramなどのSNSを分析したりすることもあります。
市場調査では、集計したデータをさまざまな切り口で分析し、全体の傾向や特徴を把握しなければなりません。統計学を身につけていれば、主に調査方法の選定やデータ分析などに活かせます。
エンジニア、技術者
エンジニア、技術者の中でも、特にAIエンジニアは統計学の知識があると強みになります。というのも、AI開発には統計学の知識が求められるからです。エンジニアが扱うプログラミング言語には、統計処理や数値計算を得意とする「Python(パイソン)」や統計解析を目的に作られた言語「R言語」があります。これらの言語を使ったAI開発の分野では、統計学の知識が活かせます。
マーケター、販売担当者
マーケター、販売担当者とは、マーケティング業務を行う人のことで、顧客データや売上データなどを分析し、売上・利益の向上につながる仕組みを作り、実行するのが仕事です。
マーケターの業務は幅広く、ウェブサイトやSNSアカウントの運営、メルマガ配信、ウェビナー(インターネット上で配信されるセミナー)やイベントの企画などがあります。
これらの実施後には、顧客のリアクションや効果に関するデータを収集して分析し、次の戦略に役立てなければなりません。統計学の知識があれば、データ分析に活かせます。
データサイエンティスト・データアナリスト
データサイエンティストやデータアナリストは、データ分析を専門とする職業です。どちらも、企業に蓄積された顧客データなどのビッグデータを活用・分析して、企業経営に役立つ情報を提供します。そのため、分析力はもちろん、ビジネススキル、ITスキルが必要です。
データアナリストは経営者への提案などコンサルタントとしての側面がある仕事が多く、データサイエンティストは高度なデータ分析を行うための仕組みづくりの仕事が多いという違いがあります。
関連記事:データーリテラシーとは?