- 主成分分析(PCA) 【イラスト図解】
主成分分析(PCA) 【イラスト図解】
英語: principal component analysis; PCA 中国語:主成分分析
主成分分析とは
互いに相関のある多数の変量を互いに無相関な少数の総合特性値(主成分と呼ばれる.)にまとめ,データを縮約する多変量解析手法.
主成分の値(主成分スコアと呼ばれる.)を座標とすることによって,多次元空間内のデータを低次元の空間に情報をあまり損なうことなく表示できる.
また,主成分ともとの変量の相関(因子負荷量と呼ぶ.)をプロットすることによって,変量間の構造が把握できる.
この意味で主成分分析は代表的なオーディネーションの手法といえる.
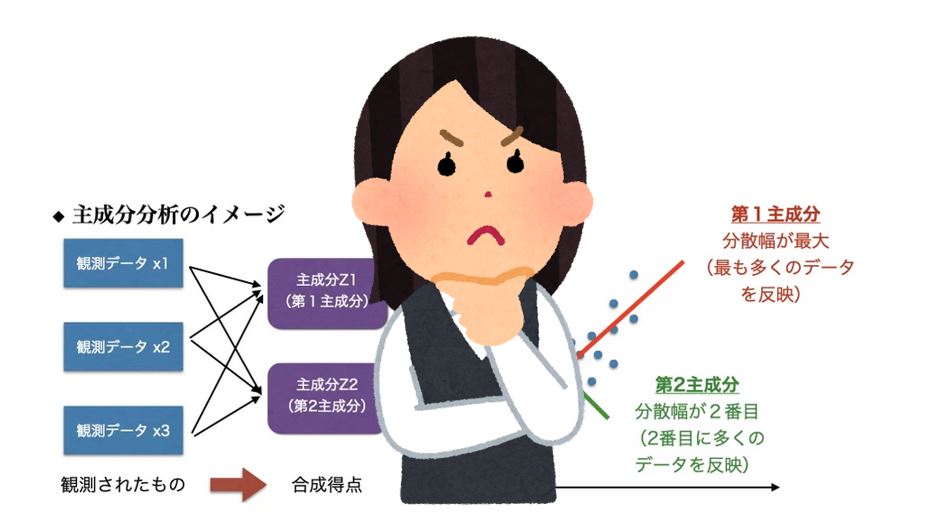
主成分はもとの変数の一次式で定義され,その各係数ベクトルは長さが1,という制約の下で次のように定められる.
第1主成分の係数ベクトルは,主成分の分散が最大となるように,第2主成分については,第1:主成分と無相関という条件の下で分散を最大とするように….
主成分の計算は,数学的には対称行列の標準型を求めることにほかならず,固有値を求めるアルゴリズムによって数値的に求められる.
もとの変数をそのまま用いるか,分散1に基準化しておくか,あるいは分散が適当な値になるように重みを付けるかによって主成分分析の結果は変化する.
どのような方針を採用するかは解析目的に依存し,一概に論じられないが,通常は分散1に基準化し,相関行列から出発することが多い.
主成分がもとの情報をどれだけ保存しているかを示す尺度として寄与率がしばしば用いられる.
これは主成分の分散をもとの変量の分散の和で除したものでありこれが1以上になる主成分を「総合
指標として意味がある」として意味づけることが多い.
寄与率を第1主成分から当該の主成分まで加えたものを累積寄与率という.
引用先:クォリティーマネジメント用語辞典 日本規格協会
わかりすく主成分分析とは
主成分分析の一手法がマトリックスデータ解析法で新QC七つ道具の中で唯一の数値データ解析法である.
何かを予測する先生あり学習ではなく、先生なし学習にあたります。
主成分とはデータの特徴を表す要素のことで、「第一主成分、第二主成分・・・」という形で表現します。
具体例で解説します。
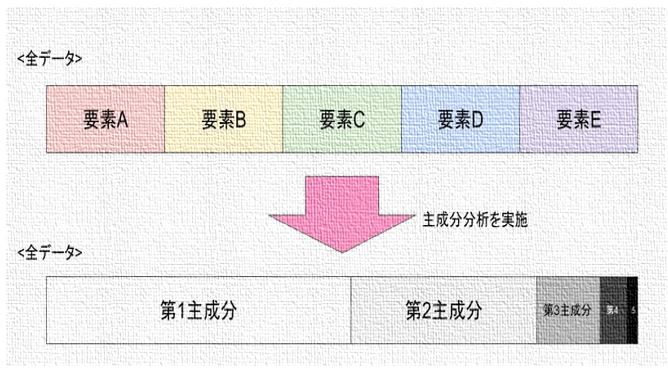
要素A~Eで構成されるデータがあります、5つも要素があると集計が大変なので、主成分分析で各要素をより少ない要素で表すことにしてみました。
分析の結果、全データを以下のように表すことができます。
5つの主成分がありますが第4と第5主成分はデータの構成要素のうち10%未満ですので、第1〜第3主成分で全データのほとんどの要素を表せることが分かりました。
このように主成分分析を実施すると、多くの変数(要素)で表されたデータをより少ない変数(要素)で表すことが可能です。
関連用語:マトリックスデータ解析法
主成分分析の利点
情報を集約しながら変数減少
主成分分析を使えばデータの情報量をなるべく減らさずに変数の数を減らすことが可能です。
主成分分析を使わずにデータの変数を絞りたい場合、いくつかの変数を切り捨てなければなりません。
しかしそれだと重要な変数も切り捨てなければならない場合が出てきます。
主成分分析は、各変数の情報をなるべく多く含むように第1主成分から順に主成分を生成していきます。
そのため通常よりも効率的に変数の数を減らすことができます。
データのグラフ化
第1主成分得点と第2主成分得点を使用することで、多くの変数を持つデータの可視化(グラフ化)ができます、通常は2変数以上含むデータを2次元でグラフ化することはできません。
しかし第1主成分と第2主成分に各変数の情報量を集約してしまえば、グラフ化が可能となります。
変数間の関係性 把握
各主成分の主成分負荷量をみることで、変数間の関係性を知ることが出来ます。
先ほどの例で上げた主成分負荷量をもう一度確認します。
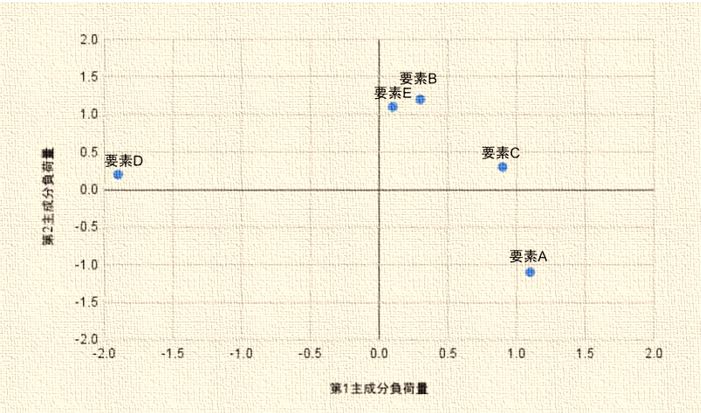
第1主成分の主成分負荷量→{要素A:1.1、要素B:0.3、要素C:0.9、要素D:-1.9、要素E:0.1}
第2主成分の主成分負荷量→{要素A:-1.1、要素B:1.2、要素C:0.3、要素D:0.2、要素E:1.1}
第1、第2主成分をそれぞれx軸、y軸としてグラフ化すると以下のようになります。
要素Bと要素Eは近い位置にあり同じような性質を表す変数であることがわかります。
以上のように主成分負荷量をグラフ化することで、変数間の関係性を考察することも可能です。
主成分分析と因子分析の違い
主成分分析と因子分析は複数の変数を少数の変数に要約するという点で似ていますが異なります。
両者の最大の違いは、新しく作成する変数の中身を事前に仮定しているか否かです。
新しく作る変数のことを主成分分析では”主成分”、因子分析では”因子”と表現します。
“主成分”は先ほどご説明したようにデータの分散が最大になるように設定されるため、すべての変数を使用して主成分負荷量を計算します。
”因子”は先にどの変数を使用するか仮定し、仮定された変数のみを使って主成分負荷量(正確には因子負荷量)を計算します。
要約すると以下の違いになります。
全ての変数を使って新しい変数(主成分)を作る→主成分分析
あらかじめ仮定した変数のみをつかって新しい変数(因子)を作る→因子分析
因子分析のほうがあらかじめ使う変数を仮定している分、作成した因子の解釈が容易です。
しかし仮定が間違っていた場合、寄与率が低くなるリスクがあります。
そのため作成する因子の目処が立っていたり、特定の因子について分析したい時は因子分析を選択することになります。
*主成分分析の詳細は下記の関連記事を参照願います。
関連記事:わかりやすい マトリックス・データ解析法 【イラスト図解】