箱ひげ図 box-whisker plot 【図解】
英語:box-whisker plot 中国語:箱线图
箱ひげ図とは
データの要約(記述)の方法として探索的データ解析において用いられる図的表示法の一つ.
層別後のデータの分布の比較を行ったり,時刻に対する分布の変化を視覚的にとらえたり,外れ値を検出するためなどにきわめて有効な手法である.
箱ひげ図の描き方と例
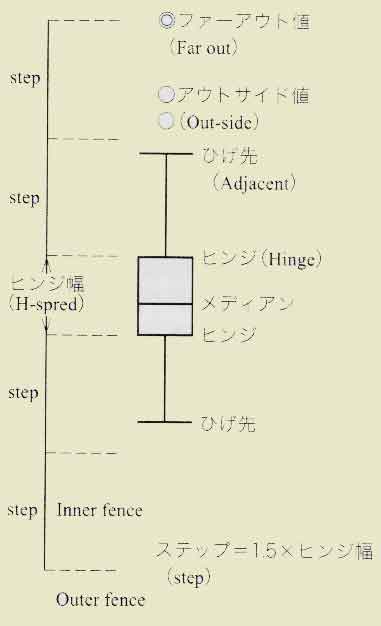
まず四分位値(上・下側ヒンジとメディアン)から「箱」を作る.ヒンジ幅(四分位差)の1.5倍をステップ(step)と呼び,ばらつきの目安とする.それぞれのヒンジから2ステップ以上離れた外れ値をファーアウト(far out)値と呼び,○で表す.
1ステップから2ステップ離れたものをアウトサイド(out-side)値と呼び,0で表す.
これらにはサンプルナンバーなどの識別子をつけておくとよい.ヒンジから1ステップ以内にあり,かつ最も離れた値をひげ先端(adjacent)と呼び「ひげ」をそこまでのばす.
なお,上記で英語を示した言葉についてはまだ定訳がない.
引用先:クォリティーマネジメント用語辞典 日本規格協会
箱ひげ図の歴史
箱ひげ図は、アメリカの統計学者 ジョン・W・テューキー(John Wilder Tukey) によって1970年代に考案されました。
● 背景と意義
テューキーは、「探索的データ解析(EDA: Exploratory Data Analysis)」 という考え方を提唱しました。これは、複雑な計算よりもまずデータを視覚的に理解することを重視した手法です。
箱ひげ図はEDAの代表的なツールであり、
-
データの要約(中央値・四分位数など)
-
比較(群間のばらつきや偏り)
-
異常値の発見
といった目的において、直感的かつ簡潔な手段として広まりました。
【EDAの目的】
EDAの目的は、以下のような**「データの構造・特徴・パターン」を発見すること**です:
| 主な目的 | 説明 |
|---|---|
| データの概要把握 | 全体の傾向(平均・中央値・ばらつきなど)を把握する |
| 外れ値の検出 | 通常の範囲から逸脱した異常なデータを見つける |
| パターンや関係性の発見 | 変数間の相関やグループ内の差を視覚的に確認する |
| 仮説の生成 | さらに詳細な分析や統計モデルを作る前の「問い」を導き出す |
| 分布の確認 | 正規分布かどうか、偏り(歪度)、尖度などをチェックする |
【EDAの特徴と利点】
| 特徴 | 内容 |
|---|---|
| 直感的・視覚的 | 数値だけでなくグラフを活用して理解を深める |
| 仮説に縛られない | 先入観なしに「まずは見てみる」という柔軟なアプローチ |
| 前処理・分析の前提作り | 欠損値、異常値、変数の分布を知ることで、その後の統計解析や機械学習の質が向上 |
【EDAと統計的推測の違い】
| 比較項目 | Exploratory Data Analysis(EDA) | Confirmatory Data Analysis(CDA) |
|---|---|---|
| 主な目的 | データの特徴やパターンの探索 | 仮説の検証(統計的検定) |
| アプローチ | 仮説なしでデータを見る | 事前の仮説に基づく検定や推定 |
| 柔軟性 | 高い(自由な視点で観察) | 低い(形式的な手順に従う) |
箱ひげ図で何がわかる?
「箱ひげ図(Boxplot)」は、データの分布を「箱」と「ひげ」で表したグラフで、データがどのあたりの値に集中しているかをひと目でわかります。
なぜ「箱」と「ひげ」?
-
箱(box):第1四分位数(Q1)から第3四分位数(Q3)までの範囲を表す四角
-
ひげ(whisker):箱の外に伸びる線で、通常の範囲のデータの最小値・最大値を示す
-
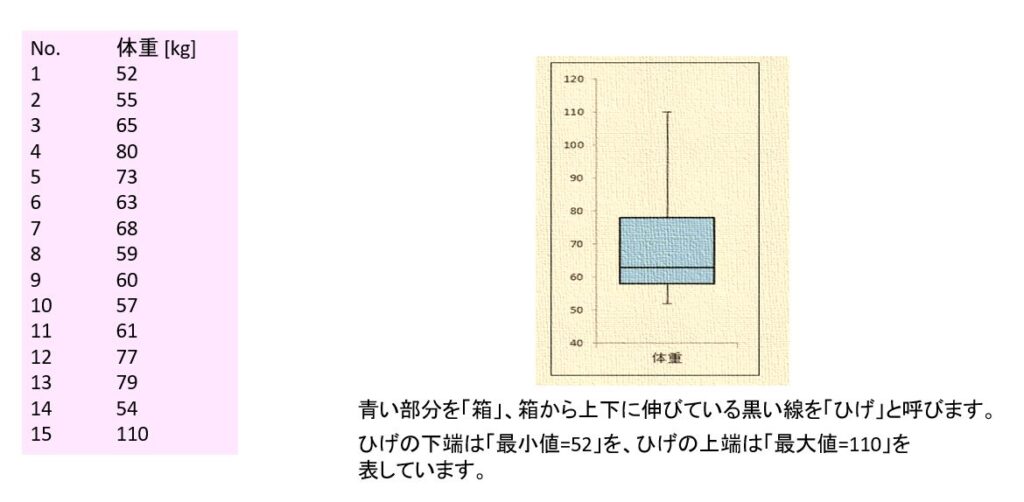
日本語では見た目がひげのようなので「ひげ」と呼ばれています。
箱ひげ図 全体の何%?
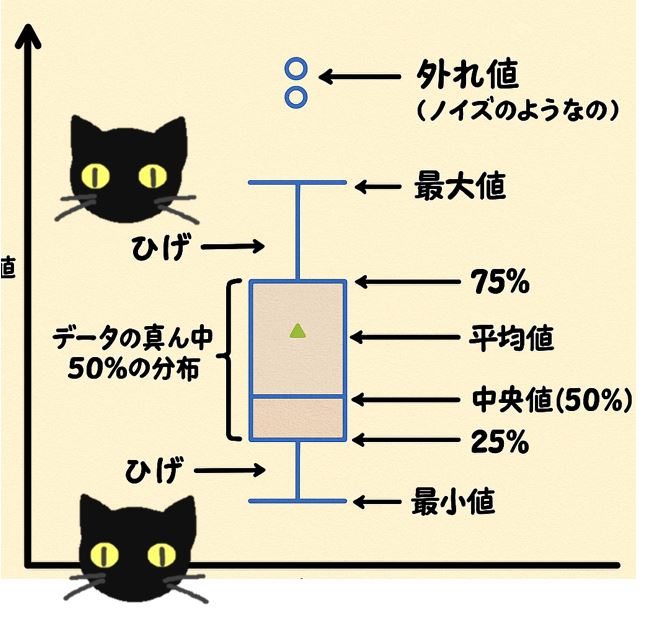
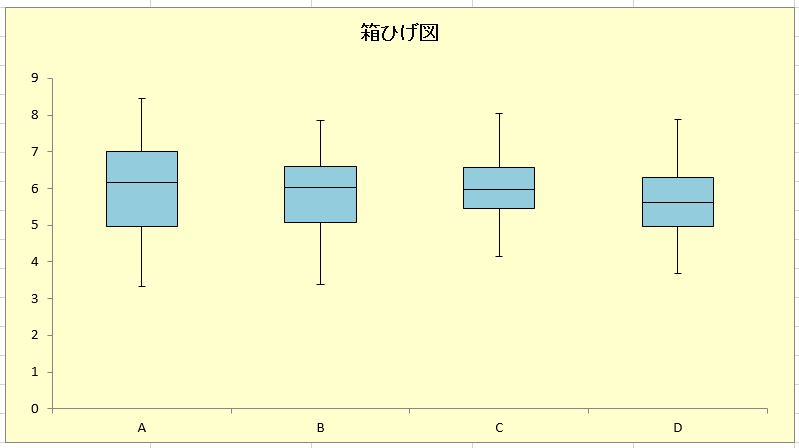
下図のような箱ひげ図を用いて、箱ひげ図の見方について解説。
箱ひげ図は長方形の「箱」と「ひげ」と呼ばれる直線で構成。
箱ひげ図は、データを大きさ順に並べた時の分布を表示。
値の軸が上向きなので、ひげの下側の末端が最小値、ひげの上側の末端が最大値を表示。
最小値と最大値の間は、4つの区間に区切られていて、それぞれの区間が全体の25%のデータを収容。
それぞれの区間の切れ目は、
箱の下底:25%目のデータ
箱の中の横線:中央値(50%目のデータ)
箱の上底:75%目
のデータを表示。
そのため、長方形(箱)の範囲にデータの真ん中50%が含んでいます、箱ひげ図は平均値を表現すること可能です、上図では緑の三角形で示されている点が平均値を表示しています。
箱ひげ図(ボックスプロット)の書き方の基本
初心者向けに箱ひげ図(ボックスプロット)の書き方の基本をやさしく解説します。手書きでもExcelやAIでも応用できます。
箱ひげ図とは?
データの分布・ばらつき・外れ値を一目で表すグラフです。
統計的には「五数要約(最小値・第一四分位数・中央値・第三四分位数・最大値)」をもとに作られます。
書き方の基本ステップ(手書きでもOK)
例としてアイス工場の製品重量データから箱ひげ図を作成する。
① データを小さい順に並べる
45, 48, 50, 52, 52, 53, 54, 56, 58, 60
② 五数要約を求める
- 最小値(min):45
- 第一四分位数(Q1):48
- 中央値(Q2):52.5(真ん中)
- 第三四分位数(Q3):56
- 最大値(max):60
③ 数直線を引く
横に0から100などのスケール線を引きます(値に合わせて調整)
④ 箱(ボックス)を描く
- Q1(48)からQ3(56)の間に長方形の箱を描く
- 箱の中に中央値(52.5)の線を引く
⑤ ひげ(線)を描く
- 箱の左端(Q1)から最小値(45)へ線を伸ばす
- 箱の右端(Q3)から最大値(60)へ線を伸ばす
⑥ 外れ値がある場合は●で表示
例:極端に小さい or 大きい値があれば箱の外に点で表示します
箱ひげ図 完成
chatGPTで自動作成した箱ひげ図。
ワンポイント解説
| 用語 | 意味 |
|---|---|
| Q1(25%) | 下位25%の境目 |
| Q2(50%) | 中央値、データの中心 |
| Q3(75%) | 上位25%の境目 |
| IQR | Q3 − Q1、箱の幅 |
| 外れ値 | 通常、Q1−1.5×IQRより下 or Q3+1.5×IQRより上 |
初心者がよくやる間違い
- 中央線を「平均値」と勘違いする → 正しくは中央値
- ひげの先を「データの端」ではなく「Q1/Q3」と思ってしまう
箱ひげ図を簡単に作るには?
箱ひげ図を簡単に作るには下記の方法があります。
- Python(matplotlib):
plt.boxplot(data)で簡単作成 - ChatGPTやAIツール:データを渡すと自動生成も可能!
- Excel:データを選択 → 挿入 → 統計グラフ → 「箱ひげ図」
エクセルでの箱ひげ図自動作成については下記を参考願いします。
エクセル 箱ひげ図自動作成
1. Excel ファイルをダウンロードします。
ファイルのダウンロード →エクセル 箱ひげ図 自動作成
使用方法:
・罫線で囲まれたセルに変数名または数値を入力。
・数値はすべて正の値である事。
・ひげの数値がない場合は空欄とする。
・外れ値には非対応。
・変数の数を増やす場合、一番右以外の列を選択後、コピーしてそのまま同じ位置に挿入の事。
・変数の数を減らす場合、いずれかの列を選択後、削除の事。
箱ひげ図の読み取り方の事例
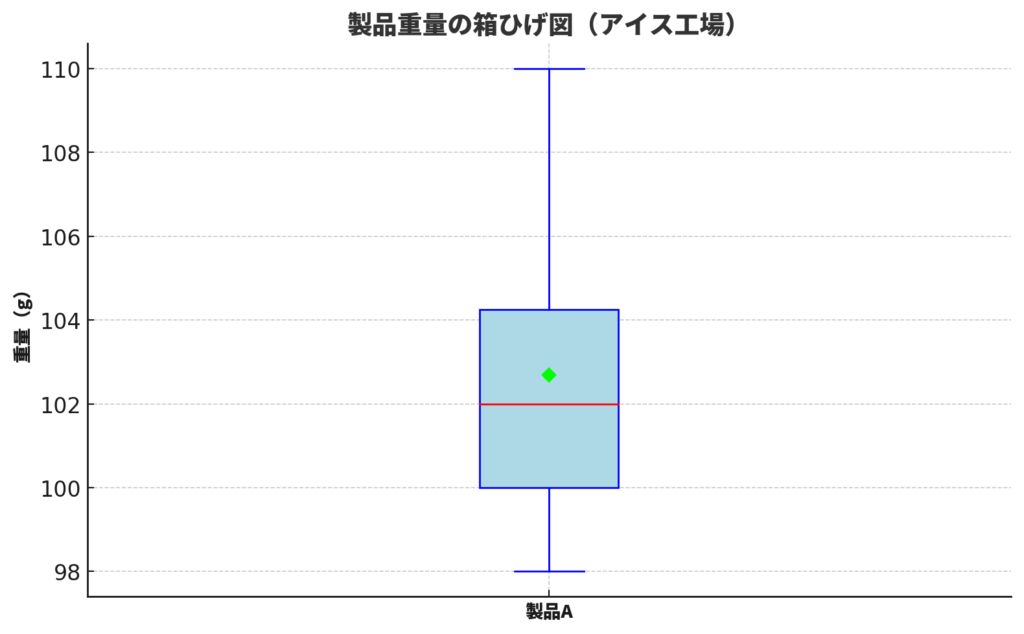
以下に、アイス工場の製品重量データをもとにした箱ひげ図の読み取り事例を示します。初心者にもわかりやすいように、ポイントを丁寧に解説します。
事例データ:アイス工場の製品重量(g)
実測データ(例)
98, 99, 100, 100, 100, 101, 101, 102, 102, 103,
104, 104, 105, 106, 108, 110
このデータを箱ひげ図にすると、以下のようになります。
箱ひげ図の読み取りポイント(アイス工場編)
| 項目 | 説明 | 読み取り結果(製品A) |
|---|---|---|
| 中央値(赤線) | データのちょうど真ん中(50%点) | 約102g:ほぼ目標値(100g)付近 |
| 箱(Q1~Q3) | 中央の50%のデータ範囲 | 100g~104g:品質のばらつきが狭い |
| ひげ(最小~最大) | 製品の最小~最大重量 | 98g~110g:想定範囲内に収まっている |
| 平均値(緑の◆) | 全体の平均重量 | 中央値よりやや右(約103g):少し右に偏っている可能性あり |
| 外れ値 | 極端に外れた値 | なし:生産は安定している |
製造現場での解釈
🔹 安定性あり:箱の幅(IQR)が狭い → 個体差が小さい
🔹 微妙な偏り:平均値が中央値より右 → やや「重め」に偏っている可能性
🔹 良品率が高い:ひげの範囲も許容内、外れ値なし → 出荷OK!
改善のヒント
- 平均が少し重い → 原材料コストに影響 → 充填機を微調整で節約
- 中央値がブレる場合 → 計量器の点検 or 作業員の熟練度チェック
- 外れ値が出たら → 機械トラブル or 異物混入を疑って原因分析!
ヒストグラムと箱ひげ図はどう使い分けます?
複数のデータを比較する必要がある場合は箱ひげ図を用いることが多いです。 逆に単一データにおける「ばらつき具合」を詳細に掴みたい場合はヒストグラムを使います。
もちろん目的に応じて箱ひげ図とヒストグラムを使い分けることは可能ですが、データの特徴を深く掴むためには両方併せて使うことをおすすめします。
箱ひげ図を使う利点・欠点
箱ひげ図を使う利点
箱ひげ図を使うことの利点は以下の3つです。
- 複数のデータを簡単に比較できる
- データの特徴をある程度理解できる
- 外れ値を見つけやすい
1つずつ解説していきます。
【利点1】複数のデータを簡単に比較できる
箱ひげ図を用いることで複数のデータを簡単に比較できます。
1回見るだけで、中央値や最小値、最大値、四分位数を把握できるため、異なるデータと比較することで、データの特徴を比較することに適しているのが箱ひげ図です。
それぞれの商品の購買の年齢層を分析する場合、箱ひげ図で比較することで、どの商品がどの年代によく買われているのかを把握できます。
【利点2】データの特徴をある程度理解できる
箱ひげ図はデータの特徴を理解することに適しています。
分析したいデータを箱ひげ図でグラフにすることで、データの25%,50%,75%の点や最大値・最小値、外れ値が把握可能です。
四分位範囲が狭いなら、中央付近の値は似たような数字が集まっているのではないかと推測が立てられます。
データを分析するとなったら、まず箱ひげ図でデータの特徴をつかむことをおすすめします。
【利点3】外れ値を見つけやすい
箱ひげ図は外れ値を見つけやすいです。
外れ値のところで説明しましたが、箱ひげ図では外れ値がひげの外の点として表されます。
外れ値があると分析結果に大きく影響するため、外れ値があるかどうかを把握しなくてはなりません。
まず、外れ値があるかないかを箱ひげ図を使って確認し、その外れ値が意味のあるデータかどうかを判断するようにしましょう。
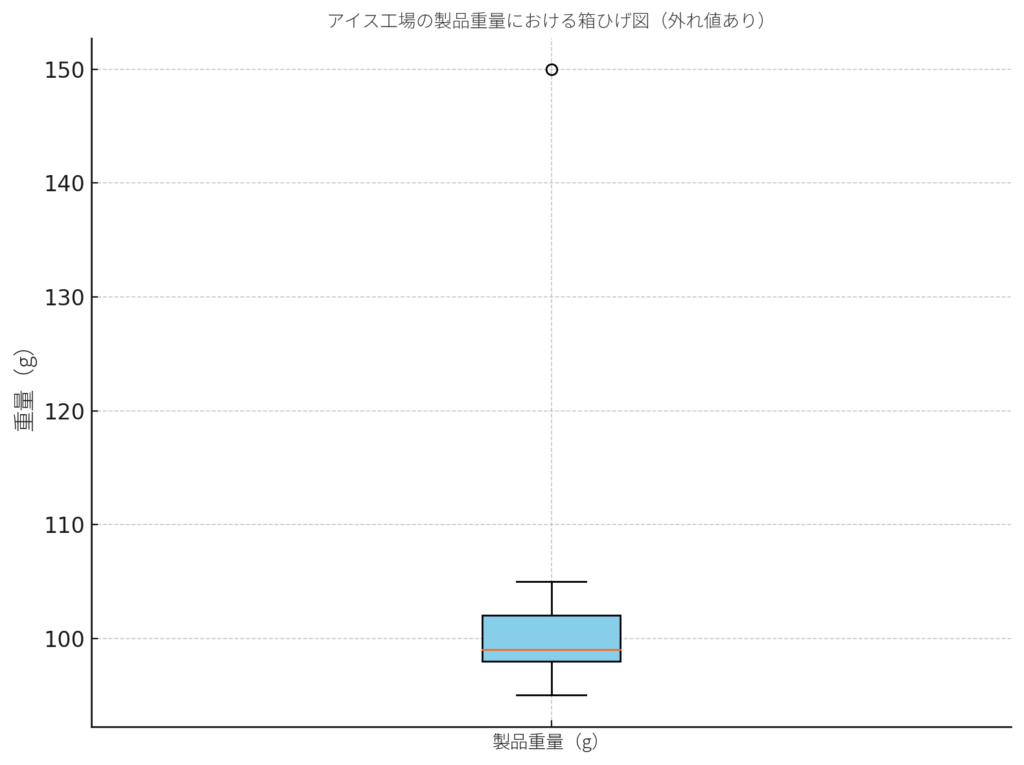
下記がアイス工場での外れ値の事例です。
通常の製品重量は 95~105g 程度ですが1つだけ150g のデータがあり、これは他と大きく乖離しています。
150gのアイスは、計量ミスや機械の異常が考えられます。
箱ひげ図を使うことの3つの欠点
デメリットは以下の3つです。
【欠点1】詳細なデータの分布を把握できない
箱ひげ図はデータの概要を把握するのに適していますが、詳細な分布は把握できません。
箱ひげ図によって四分位数を把握できますが、四分位数間でどのようなデータの増加が起こっているのかを把握できないのです。
データの概要は箱ひげ図を使って把握し、詳細なデータの分布は別のグラフを使う。
【欠点2】データの数によって見え方が変わる
データの数の違いによって、箱ひげ図の見え方は大きく変わります。
データの数が少ないと、1つ1つの数値が大きな意味を持ち、データが1つ追加されるだけで箱ひげ図が大きく変わってしまいます。
また、データの数が少ないとデータの幅が狭くなるため、少しでも極端な値を取れば外れ値とみなされることもあります。
データの数を大きくしたほうが箱ひげ図は安定するため、データは多く用意する。
【欠点3】データの比較に注意が必要
箱ひげ図で複数のデータを並べて比較する時には注意が必要です。
それぞれの箱ひげ図でデータの範囲が極端に異なると適切に分析できない可能性があります。
例えば、身長の分布の箱ひげ図と体重の分布の箱ひげ図を比較する。
身長は数値が100を超える分布なのに、体重が50台の分布になるため、体重のほうが低い値の分布だと決めつけてしまいます。
2つの違いは単位です。
必ず単位をそろえること、単位がそろっていても極端に値に分布が違う場合は注意します。
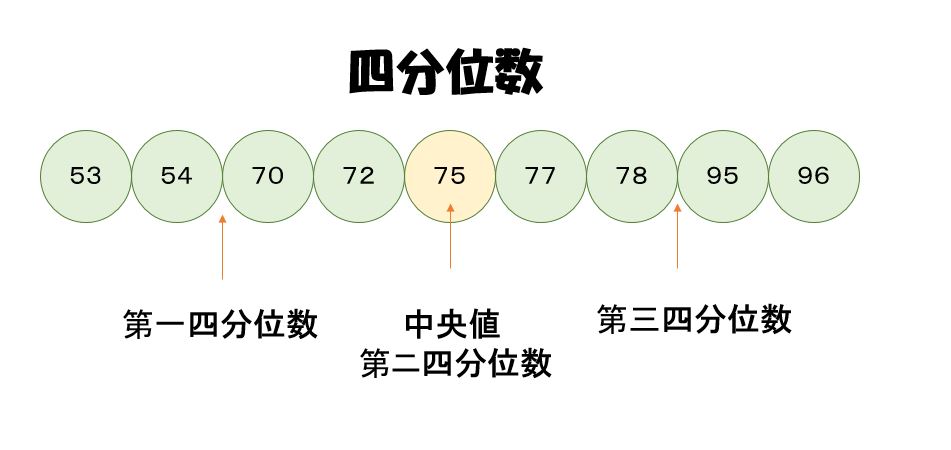
四分位数とは? :データの区切り
四分位数は、データを小さい順に並べたときにデータを4等分する数値。
四分位数は箱の両端の線と中央値から構成される数になります。
それぞれを第1四分位数、第2四分位数、第3四分位数と言い、以下のような役割を持ちます。
- 第1四分位数:データの25%の所を示す役割
- 第2四分位数:データの50%の所(中央値)を示す役割
- 第3四分位数:データの75%の所を示す役割
箱ひげ図の見方、活用事例
箱ひげ図は初心者でも箱ひげ図を活用することで、「感覚ではなくデータで判断」できるようになります、品質管理・教育現場・業務改善など、あらゆる分野での「現状把握と改善提案」に役立つ便利なツールです!。
下記の箱ひげ図を活用した事例を記載します。
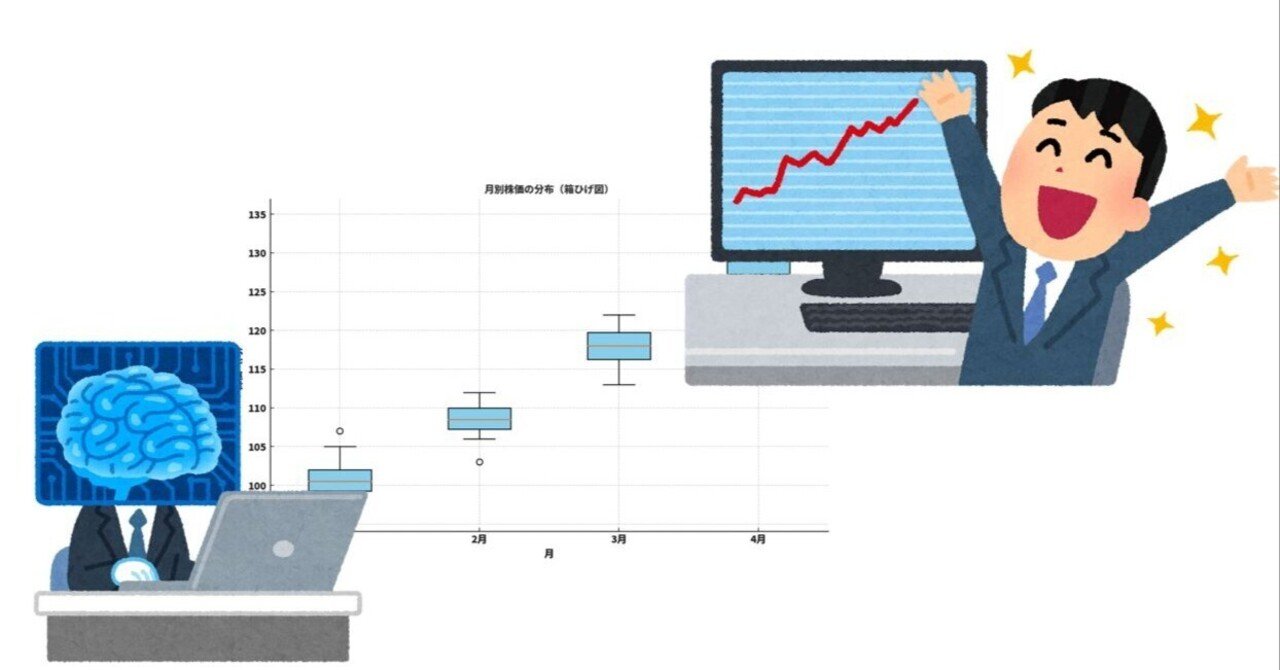
■ 活用事例①:株価の複数期間での比較
箱ひげ図は、平均だけでは見落とされがちな「データのばらつき」や「外れ値」を可視化し、株価のリスクやトレンドの兆候を直感的に把握できるツールです。特に「複数期間での比較」や「複数銘柄の特性分析」に強みがあります。
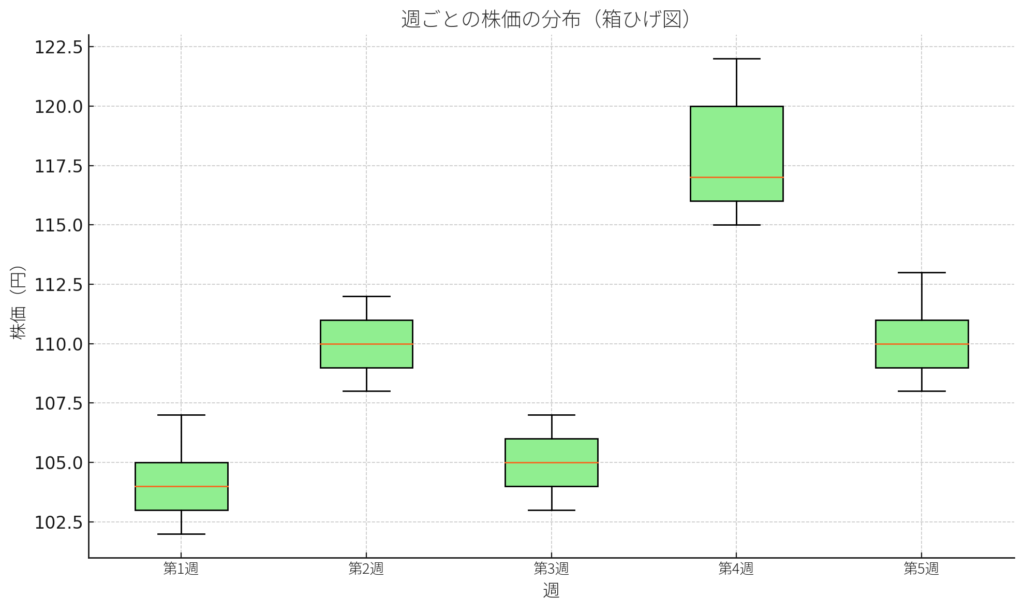
下記は週ごとの株価の分布(箱ひげ図)を示した図です。各週(月〜金)の株価のばらつきを箱ひげ図で可視化しています。
図の読み取りポイント
| 週 | 特徴 |
|---|---|
| 第1週 | 中央値が103〜104円で安定。ばらつきも小さい。 |
| 第2週 | 全体的に株価が高く、110円前後で安定。 |
| 第3週 | 徐々に株価が下落傾向。分布が下方向に偏っている。 |
| 第4週 | 株価が急騰し、外れ値はないが全体的に高い。 |
| 第5週 | ボラティリティ(ばらつき)が大きく、読みにくい展開。 |
株価予想への応用方法
| 活用方法 | 内容 |
|---|---|
| 株価のボラティリティ評価 | ひげの長さで価格変動の大きさを視覚的に確認できる |
| 安定銘柄と変動銘柄の分類 | 箱が小さい=安定株、箱が大きい=変動株という目安が作れる |
| 外れ値の検出(急騰・急落) | 突発的な値動き(イベント発生など)のサインとして利用可能 |
| 投資戦略の構築 | 安定株には長期投資、変動株には短期トレード戦略を選定するための判断材料 |
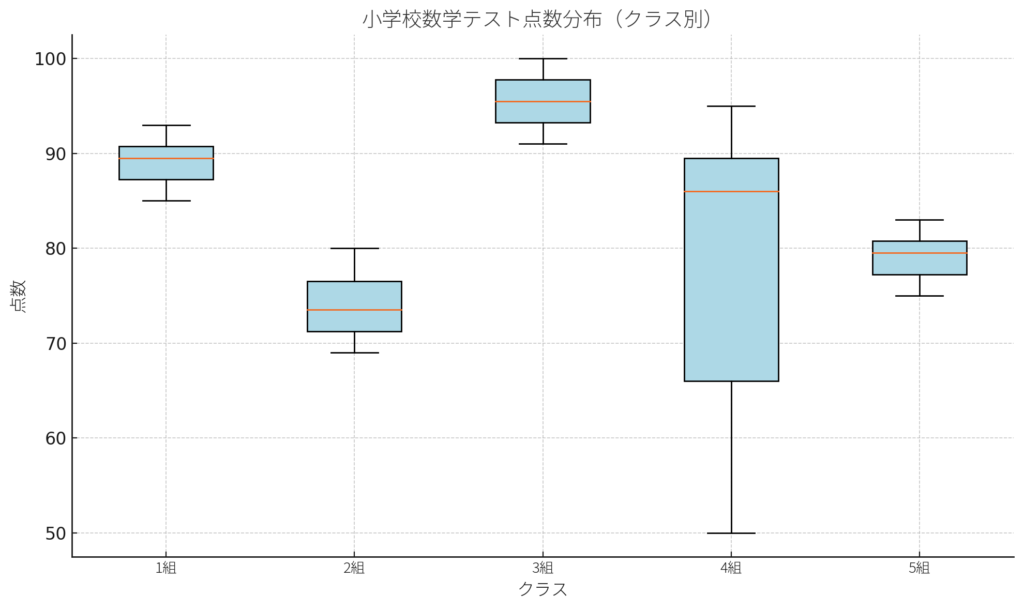
■ 活用事例②:小学校のテストの点数分布
背景:ある小学校の先生が、同じ数学テストを複数のクラスに実施した。
目的:各クラスの理解度や点数の偏りを視覚的に把握したい。
➤ 活用方法:
各クラスの点数を箱ひげ図で比較。
➤ 読み取りポイント:
-
中央値が高いクラス → 成績が全体的に良い。
-
箱が大きいクラス → 成績に差があり、個別支援が必要。
-
外れ値が多いクラス → 特に高得点や低得点の子がいる。
➤ 改善アクション:
中央値が低いクラスには補習授業を実施。外れ値があるクラスには個別指導を検討。
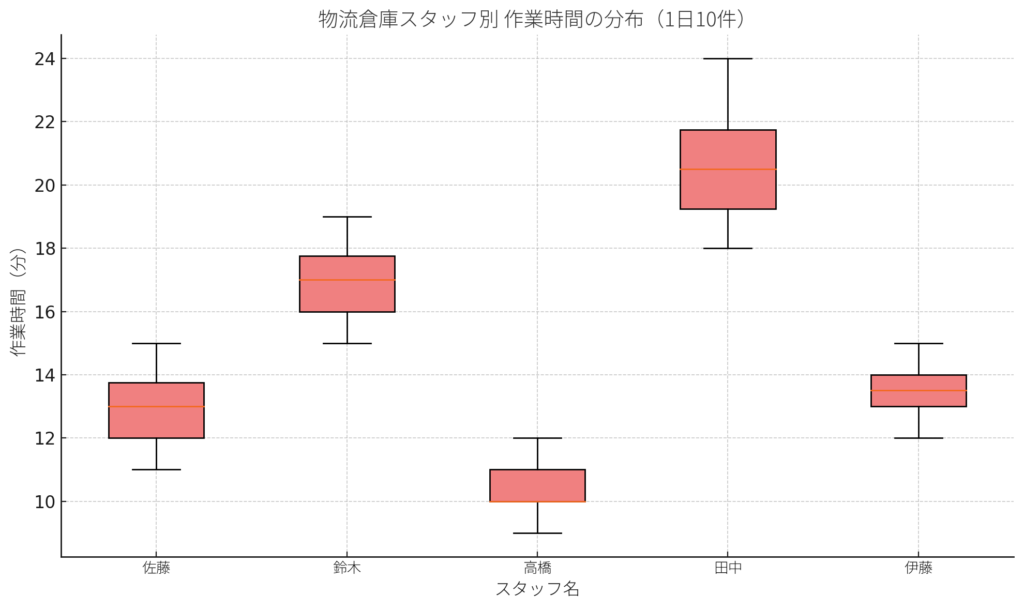
■ 活用事例③:物流倉庫の作業時間の見える化
背景:物流倉庫のスタッフのピッキング作業にかかる時間を分析。
目的:誰が早いかではなく、「ばらつき」や「標準化できるか」を見たい。
➤ 活用方法:
スタッフごとに1日10件の作業時間を測定し、箱ひげ図にまとめる。
➤ 読み取りポイント:
-
ばらつきが小さい人は標準作業に近く、指導役に適任。
-
外れ値が頻繁な人は不慣れ or 作業手順にミスの可能性。
-
全体的に箱が大きい → 作業手順のばらつきが多く、マニュアル改善が必要。
➤ 改善アクション:
優秀な作業者の動きを参考に、ピッキングマニュアルを改訂 → 全体の作業時間が短縮。
箱ひげ図の教育・医療・農業・スポーツ・ビジネス等での活用
箱ひげ図は 「平均値では見えない“バラつきと偏り”を一瞬で見せる」事ができるの教育・医療・農業・スポーツ・ビジネス・社会調査・IT分野まで幅広く活用ができる!
教育(学力分析・クラス比較)
事例
- 学力テストのクラス別比較
- 教科別の得点分布の差
- 入試の志願者スコアの比較
ポイント
- 平均点だけでは見えない“偏差の大きさ”が分かる
- 優秀層・下位層・外れ値(突出した生徒)が可視化
→ 学力の層別・指導計画の作成に直結。
② 医療(治療効果比較・健康データ分析)
事例
- A薬とB薬の効果比較(血圧、血糖値の分布)
- 病院別の待ち時間分布
- 診療科別の検査数値のばらつき
ポイント
- 医学研究でもよく使われる基本グラフ
- 平均値だけでは隠れる“個体差”を可視化
- 外れ値=異常値の早期発見にも有効
③ 農業(作物サイズ・収穫量の比較)
事例
- 農家ごと・畑ごとの収穫重量のばらつき
- イチゴ・リンゴなど果実の直径・重量の比較
- 施肥方法A/B/Cによる品質差
ポイント
- 規格選別(秀品・良品・規格外)の精度向上
- 気温・水量・肥料条件などの層別分析に最適
④ 食品業界(製品品質・味の評価)
事例
- 官能検査の評価分布(甘味・酸味・食感)
- 店舗別の提供量のばらつき(ラーメンの麺量など)
- 製造日による風味の分布比較
ポイント
- 主観評価(官能)を“分布で見える化”できる
- テイスターの癖(外れ値)の把握にも役立つ
⑤ スポーツ(選手比較・パフォーマンス分析)
事例
- 走力・打率・スイング速度の分布比較
- チームごとのフィットネス測定値
- 陸上選手のラップタイム比較(コース別)
ポイント
- 個々の選手の安定性がわかる
- チーム内の“バラつき”が一発で可視化
- 戦略立案・選手育成にも有効
⑥ 金融(株価・リスク分析)
事例
- 銘柄別の1日の価格変動幅分布
- 投資ファンドごとのリスク比較
- UI(ユーザ投資層別)の損益のばらつき
ポイント
- 平均リターンより“リスク幅”が重要な投資では超有効
- 外れ値=暴落・急騰の影響が見える
⑦ ビジネス(売上・接客・サービス品質)
事例
- 店舗別の売上分布
- 1ヶ月の顧客満足度スコアの比較
- 配達時間のばらつき比較
ポイント
- 「平均値は同じなのに、ばらつきが全然違う」を見える化
- サービス品質改善の判断材料に
⑧ 不動産(家賃・土地価格の比較)
事例
- 地域別の家賃相場の箱ひげ図
- 新築/中古の価格分布
- 駅徒歩距離別の価格比較
ポイント
- 価格の上限・下限・外れ物件を一目で把握
- 投資や住居選びの判断材料になる
⑨ 飲食店(レビュー分析・商品品質評価)
事例
- 店舗別の食べログ評価の分布
- メニューごとの評価比較
- Uber Eatsの配送時間のばらつき
ポイント
- “安定して高評価”か
- “評価のバラつきが激しい店”か
が直感でわかる
⑩ IT/アプリ(ユーザーデータ分析)
事例
- アプリの起動時間の分布
- サーバー応答時間の比較(A/Bテスト)
- アプリの利用時間の層別分析(年代・端末別)
ポイント
- システムの“応答時間の安定性”を評価できる
- 改善前後の比較にも最強
⑪ 社会調査(所得・労働時間・幸福度のばらつき)
事例
- 都道府県別の家計収入分布
- 労働時間のばらつき
- 男女・年齢層ごとの所得差
ポイント
- 社会格差や層別の違いが可視化
- 政策立案・行政資料にも使われる
⑫ 教育・心理学(テスト・アンケート評価)
事例
- ストレススコアの分布
- アンケート評価のばらつき
- 心理学実験のグループ差
ポイント
- 外れ値の分析で個別支援がしやすい
- グループの安定性が見える
箱ひげ図作成時の注意点
箱ひげ図を作成するときの注意点を、初心者にもわかりやすく解説します。以下のポイントを押さえることで、誤解のない正確な分析が可能になります。
箱ひげ図作成時の注意点(初心者向け)
① データの数が少なすぎないか?
- 注意点:データが5~10個程度しかないと、四分位数や外れ値の判断が難しくなります。
- 対策:最低でも20個以上のデータがあると、信頼性のある箱ひげ図になります。
② 外れ値の扱いをどうするか?
- 注意点:箱ひげ図では、「Q1-1.5×IQR」未満 または 「Q3+1.5×IQR」超の値を外れ値として●で表示します。
- 対策:外れ値を自動的に除外しない。なぜその値が出たのかを確認し、現場や背景と照らし合わせて判断することが大切です。
③ 単位・スケールを統一しているか?
- 注意点:比較するグループで単位(例:gとkg)が違っていると、誤解を生みます。
- 対策:全てのデータの単位や尺度を統一し、必要があれば軸に単位を明記しましょう。
④ 項目ラベルや凡例が分かりやすいか?
- 注意点:ラベルや凡例が不十分だと、「何の箱ひげ図なのか」読み手に伝わりません。
- 対策:
- 横軸には対象グループの名前(例:ラインA・ラインB)
- タイトルや補足に比較内容や目的を記載(例:「アイス重量の分布比較」)
⑤ 軸のスケールが適切か?
- 注意点:縦軸(Y軸)のスケールが極端だと、ばらつきが強調・過小評価されます。
- 対策:比較グループ間で同じスケールを使用し、誤解を避ける。
⑥ 外れ値の記号が見やすくなっているか?
- 注意点:外れ値が●や×などで表現されていない、または小さすぎると見落とされます。
- 対策:外れ値は目立つ色や形で明示し、「外れ値あり」の凡例を入れるとベスト。
⑦ 中央値と平均値を混同しない
- 注意点:箱ひげ図は中央値(真ん中の値)を示します。平均値ではありません。
- 対策:レポートや説明資料では「中央値です」と明記し、必要なら平均値と併記する。
⑧ データの分布が偏っていないかを意識する
- 注意点:箱ひげ図では、箱の位置やひげの長さが左右非対称な場合があります。
- 対策:偏り(例えば「中央値が下寄り」など)にも注目して、正規分布ではない可能性も考慮する。
このように、箱ひげ図を正しく・見やすく・伝わるように作成することが、データの意味を正確に伝えるための第一歩です。
*AI chatGPTを使用すればデーターを与えれば直ちに箱ひげ図が作成されて解釈及び改善提案も回答させます、但し 最終的に判断するのは「人」であり、正しいプロンプト文を指示するためには『箱ひげ図の作成、分析の基礎』を学ばなければいけません。
下記が参考になる記事です。

まとめ
箱ひげ図を活用すると現場の「見えないバラつき」がひと目で見える化できます。
アイス工場のような定量管理が命の現場では、箱ひげ図はとても強力なツールです。
又、『箱ひげ図での株式投資での成功事例』をnoteに投稿しました、ご参考 願いします。