3分で分かる! データーリテラシー資格 概要解説
「データーリテラシー資格」という特定の名称の資格は、一般的には認知されていません。しかし、データリテラシー、つまりデータを理解し、活用する能力を証明するための資格はいくつか存在します。
データリテラシーに関連する主な資格
- データサイエンティスト検定™ リテラシーレベル (DS検定®★):一般社団法人データサイエンティスト協会が主催する、データサイエンスに必要な基礎知識やスキルを証明する資格です。見習いレベルの実務能力や、数理・データサイエンス・AI教育のリテラシーレベルの実力を測ります。
- 統計検定:一般財団法人統計質保証推進協会が実施する、統計に関する知識や活用力を評価する検定です。データサイエンスの基礎となる統計学の知識を体系的に習得できます。データサイエンス基礎(DS基礎)、データサイエンス発展(DS発展)、データサイエンスエキスパート(DSエキスパート)などの種類があります。
- G検定(ジェネラリスト検定):一般社団法人日本ディープラーニング協会(JDLA)が実施する、AI・ディープラーニングに関する基礎知識を問う検定です。データ分析においてもAI技術の活用が進んでいるため、関連性の高い資格と言えます。
- Python 3 エンジニア認定データ分析試験:Pythonのデータ分析ライブラリを用いた分析スキルを証明する資格です。Pythonはデータ分析で広く用いられるプログラミング言語であり、実践的なスキルを証明できます。
- データサイエンス数学ストラテジスト:データサイエンスに必要な数学の知識を評価する資格です。中級・上級があります。
- CBAS シチズン・データサイエンティスト級:データに基づいた意思決定や問題解決を行うための基礎的な知識を評価する資格です。
データリテラシー資格を取得するメリット
- スキルの証明: データに関する知識や分析能力を客観的に証明できます。
- 就職・転職の有利性: データ活用能力が重視される現代において、就職や転職活動で有利になる可能性があります。
- キャリアアップ: データ分析スキルを向上させることで、より高度な業務に挑戦できる機会が増えます。
- 業務効率の向上: データを正しく理解し活用することで、より効率的で効果的な業務遂行が可能になります。
- 論理的思考力の向上: データに基づいた判断を行う訓練を通じて、論理的な思考力が養われます。
- データに基づいた意思決定: 客観的なデータに基づいて意思決定を行うことができるようになります。
ご自身の目的やスキルレベルに合わせて、適切な資格の取得を検討することをおすすめします。
データーリテラシーとは?
統計データーを扱う能力(収集、分析、検証等)であるデータリテラシーは物事の本質を明らかにしたり、目的を達成するための解決策を効率的に知ることができます。
一方、その能力を悪用すれば社会、人を騙し、社会生活を混乱させて人を不安に陥らせます。
よって、統計データーに騙されない為にはデータリテラシーを学ぶのが最も効果的な対策法です。
データリテラシーは英語でData literacyです。
「リテラシー」という言葉に関しては、例えばデジタル大辞泉によれば以下のような意味だとされています。
1)読み書き能力。また、与えられた材料から必要な情報を引き出し、活用する能力。応用力。
2)コンピューターについての知識および利用能力。→コンピューターリテラシー
更に詳しい英和辞典「ランダムハウス英和辞典」{小学館}を引くと第2義として「教養があること,教養」とある。
昔は読み書きができることがすなわち教養があることであったが現代では文章を読み書きできるだけでは教養があることにはならない、コンピューターを使えなければ日常生活に支障をきたす。
データリテラシーも同様にもコンピュータでデーターの作成、評価するだけでは教養があることにはならない、すべてのものごとを自己判断しなければならない。
高度情報通信社会の時代にはデータを客観的に正しく扱うスキルがなければだれも教養のある人とは見なしてくれず、詐欺に遭遇し大きな負債を負うことにもなりかねない。
広義のデータリテラシーはデータの集めかた、集めたデータの処理の仕方、データの表示や蓄積のしかた全般を含みます。つまり、データを作成し、提示する側の能力も含んだ意味となります。
狭義のデータリテラシーの意味は「データをどのように読んだらいいのか」「データにごまかされないためには」といった観点から作成を含まないデーター活用能力を育成する事です。
データリテラシーを悪用すれば情報を操作でき、人を騙すことができます、データーで騙されない為にはデータリテラシーを学ぶことが必須です。
以下に「データリテラシー」という言葉の 英語・中国語・スペイン語での表現を一覧表にまとめました。
| 言語 | 表記 | 読み・補足 |
|---|
| 🇯🇵 日本語 | データリテラシー | 情報を正しく読み解き活用する力 |
| 🇺🇸 英語 | Data Literacy | リテラシー = 読み書き能力、情報理解能力 |
| 🇨🇳 中国語(簡体) | 数据素养(Shùjù sùyǎng) | 「素养」は教養・リテラシーの意 |
| 🇨🇳 中国語(繁体) | 數據素養(Shùjù sùyǎng) | 台湾・香港圏での表記 |
| 🇪🇸 スペイン語 | Alfabetización de datos | 「Alfabetización」は識字力の意 |
データサイエンスとは
データリテラシーとデータサイエンスは混同しやすく、どちらも定義が決まっていません。
データサイエンスとは、数学や統計学、機械学習、プログラミングなどの理論を活用して、ビックデータの分析をし、将来の予測、商品の売り上げ予測等の有益な情報を導き出す学問のことを言います。
そして、データサイエンスを実行する者を「データサイエンティス」と呼んでおり、求められる能力は
①ビジネス力(ビックデータを活用しビジネスに活かす)
②ITスキル(ビックデータが保存されデーターベースを管理し、高速化する)
③統計解析スキル(ビックデータを統計処理し、視覚化する)です。
データリテラシーとデータサイエンスの違い
データリテラシー、データサイエンス どちらも定義が定まっていませんが簡単に説明するとデータサイエンスはデータを収集し処理するための手法、そのための数学的知識、コンピューターソフトウェアの使いかた、ビジネス活用などからなります。
それに対してデータリテラシーは統計処理する以前のデータに対する扱い方に重きを置きをおきます、例えばデーターのサンプリング、調査方法等です。
データリテラシーは、データサイエンスの一部を支えており、統計解析スキル(ビックデータを統計処理し、視覚化する)に該当します。
データリテラシーのメリット
データリテラシーを学ぶことによりデータを読む能力、分析する能力、活用する能力、論理的に用いる能力が養われます。
データを読む能力
データを読む能力は、そのデータから何が得られるのかを理解できる読解能力です。
データは、数字の羅列や表、円グラフや棒グラフなどさまざまな形式で示されます。これらデータから、今必要なデータを取捨選択してあなたの業務や判断を裏付けるデータを読む能力はそのデータの集まりに何が示されているのかを俯瞰的にとらえ、必要なデータを判断するものです。
データを分析する能力
データを分析する能力とはデータを数値やグラフなどを用いて分析し本質を引き出す洞察力、インサイト(Insight)の事です。
例えば、Webサイトへのアクセス解析でどのページにどの程度のアクセスがあったかを分析する方法を知ったりどのような記事を掲載すればアクセス数が伸びるのかを検証する方法を学んだりすることが挙げられます。
もちろん、Webサイトに限らず、製品別の売上や、営業方法(顧客へのアプローチ)をデータ化して分析するなど、データ分析にはさまざまな分野があります。
必要なデータを集めて分析する能力は、データリテラシーに含まれるのです。
データを活用する能力
データを活用する能力とは、データから得た情報に基づいて生産的な行動を取る能力です。
例えば、営業活動において、どのようなアプローチをすれば売上が伸びるのかという分析結果を得られた場合、そのデータを基に自身の営業方法を変えることもデータを活用した行動だといえます。
あるいは、年間を通してどのような時期にどのような商品の売上が伸びるのかを把握して、時期に合わせて仕入れの数を調整したり、キャンペーンを打ったりするなどの施策も、データを活用する能力なのです。
データを論理的に用いる能力
データを論理的に用いる能力とは、「それが正しい」ことを論理的に伝えられる能力です。
なぜそのような行動をとったのか、なぜそれが必要なのかについての理由を、データを用いて論理的に説明することで説得力がでます。
例えば、「なぜその行動をとったのか」という質問に「経験則から」と答えても説得力は弱いのですが、「このデータに基づくとこのような予測が立てられる」というソースデータがあれば、説得力は何倍にも増します。
このように、データを用いて理由を伝えられる能力も、データリテラシーだといえるのです。
データーリテラシー基礎
データーリテラシーの基本は「データーの変化を検知する」「データーを比較する」「データーを分析する」「データーを予測する」の四つです。時系列でデータの変化をみたり、他のデータと比べたり、データ対象を分けて考えたりしながら、その中にどのような特徴や法則があるのかをみていきます。
変化とはあるモノが一つのある状態・位置から、他の状態・位置に変わることであり、具体的な使い方の事例は”温度が低くなると水は液体から個体に変化する。”
比較とはあるモノと別のモノの状態・位置の異なっている部分やその差異の程度などを見定めること、具体的な使い方の事例は”人と動物を比較するとその違いは言葉である。”
分析とは物事を分解して(細かな要素に分けて)、その性質、構造などを明らかにすること、具体的な使い方の事例は”不良原因を分析する。”
推測とはある既知の事柄をもとにして未知の事について見当をつけること、具体的な使い方事例は”分析結果を基に○○を推測する”
データーリテラシーの目的
多くの場合,我々は不確実性をもつデータ(測定誤差、サンプルリング誤差等)に基づいて計算し、平均値、標準偏差等の数値情報を得て母集団に関するモデリングを行う。
そして、時系列毎の推移および他の母集団との比較をしてGap(差)を検証し、分析してその差が発生するメカニズムを究明するのがデーターリテラシーの目的である。
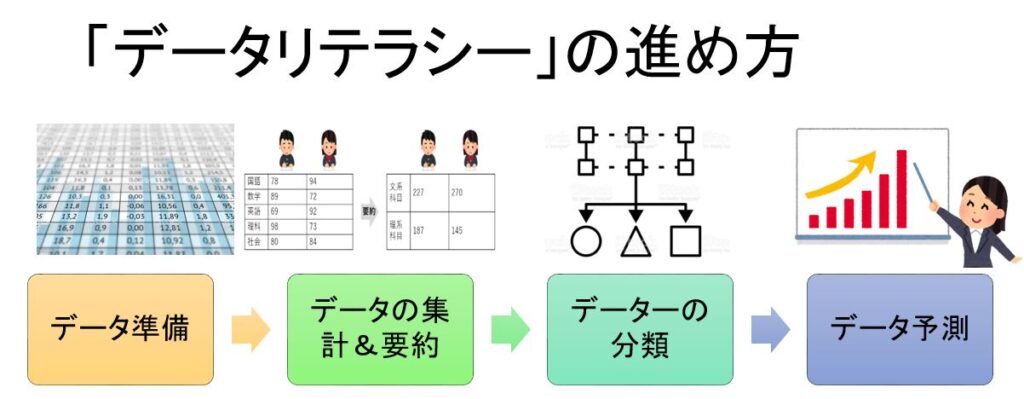
「データリテラシー」の進め方のステップは第一に有効なデータを集め、データベースをつくる。第二に集まったデータをもとにデータの集約&要約。第三にデーターの分類、第四に分析をもとに予想や予測を行うことです。
データ準備:データーベースの作成
データーサイエンスでデーター分析を行い場合、初めに必要なデーターを集め、データーの特徴、性質を知り、適切な分析ができるようにデーターベースを整形します。
自分が分析に使いたいデーターどうような過程を経て作成されたかを知ることが大切です、素性がわからいデーターを利用すると間違った結果を出します。
データーの作成別 分類
作成方法別にデータを大きく分類すると調査データーと非調査データに二つのタイプに分けることができます。
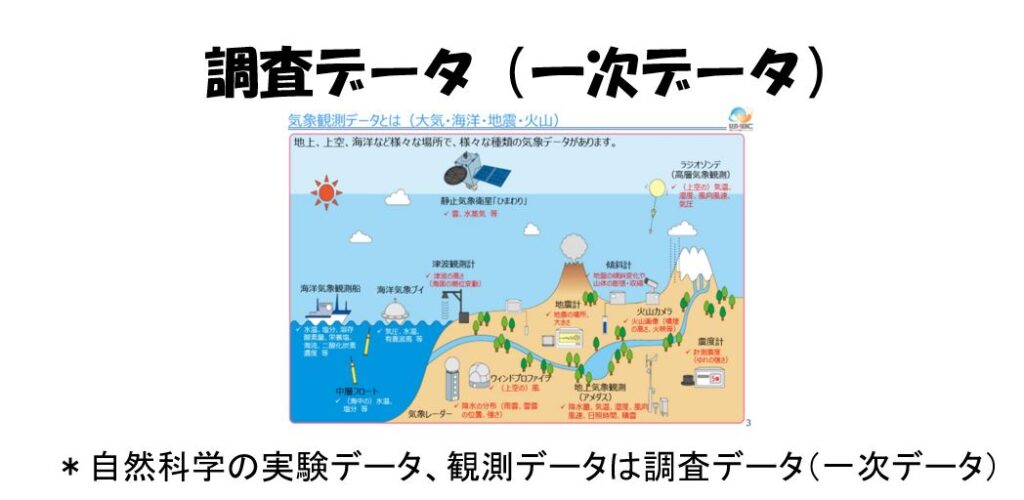
調査データ(一次データ)
調査データ(一次データ)とはデータを分析したい人が自分自身で調査を行って作成するタイプのデータです。
自然科学の実験データ、観測データは調査データ(一次データ)です。
非調査データ(ニ次データ)
非調査データ(ニ次データ)とは直接、自分自身が調査や実験、あるいは観測を通じてデータを作成するのでなく、第三者である公的機関や研究機関が作成したデータです。
各機関が調査を通じてデータを作成する場合もありますが、ネットのアクセスやコンビニでの買い物、役所への登録など、別の目的で行った結果を情報源として編成されたデータも多く含まれます。
非調査データ(ニ次データ)には下記のようなものがあります。
POSデータ
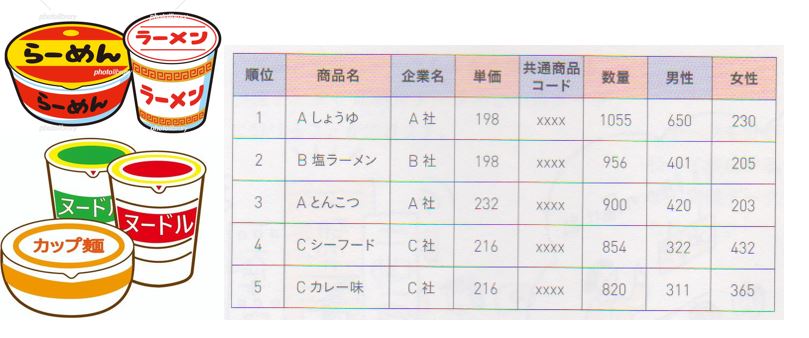
・コンビニで買い物をした場合→POSデータ POSシステムは、コンビニを始め多くの小売販売店で導入されています。
POS(Point of Sales)とは「販売時点」という意味で顧客がレジで買い物の精算をした時点で、購入された商品の価格や数量を集計してデータが作られます。
下図は全国展開するコンビニチェーンのある1日のカップめんの購入情報を集計した結果が示されています、購入の際に顧客がコンビニで使用可能なポイントカードを利用すると顧客の性別や年齢層なども購入履歴にリンクされ、販売店にとって有益な情報が提供されます。
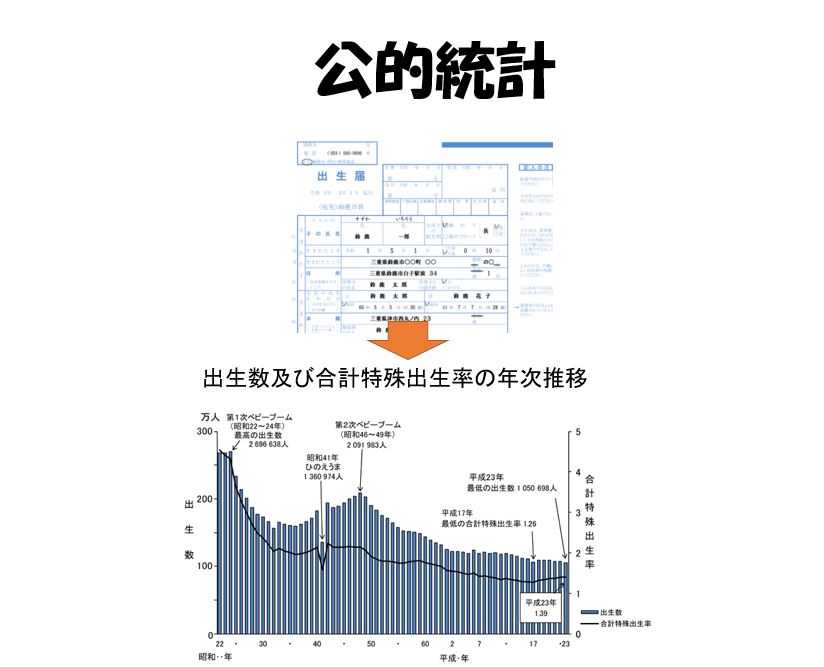
公的統計(業務統計)データ
データを作成するのは民間企業や個人だけではありません。政府や自治体もさまざまなデータを作成しています。むしろ政府や自治体のほうが主要なデータ作成の主体であるとも言えます。
政府が作成するデータを「公的統計」と言いますがよく知られている国勢調査のような「調査統計」だけでなく、さまざまな行政上の届出や申請を通じて得られた情報を集計してデータを作成する場合もあります、このような公的統計を「業務統計」と言います。
下図は、「出生届」のサンプルです。出生届は子どもが生まれた場合、市役所に届けを出すための書類ですが、そこに記載された情報は厚生労働省で集約され、1年間の出生数などの情報が「人口動態統計」という名称のデータとして公表されています。
データーの情報量別 分類
データーの情報量別に大きく分類するとビックデーターと非ビックデータに二つのタイプに分けることができます。
ビッグデータ
ビッグデータという名前から、「大規模なデータがビッグデータだ」というイメージがありますが、それだけではビッグデータとは言えません。
より正確に言うならば、ビッグデータはICT(情報通信技術)を通じて、絶えず作成・収集・蓄積が可能な「多種・多量なデータ」ということになります。
ですので、通販サイトの書籍データやPOSシステムの事例は、このようなビッグデータの条件に合致しています。
例えば通販サイトで商品を購入しようとすると、検索した商品のページに、関連商品などの情報が表示されることがあります。
これは通販サイトの購入を通じて、常時得られる顧客の購入データの分析によって予測されたものです。
このようにWeb上で常時デ¬夕が更新されているタイプのデータはビッグデータに含まれます。
非ビッグデータ
ビックデータに対し調査データ、実験データ、業務統計などは非ビックデータです。
非ビックデータの特徴はその多くが母集団(調査対象全体)と標本(サンプル)という関係に基づいてデータが得られているため、実際に得られるデータについてランダムネスができる利点があります。
データーランダムネスとは、データ(標本)が知りたいすべての対象(母集団)からランダ厶に抽出きれているということです。
これによって、標本に対して可能な限り母集団の特徴や構造を忠実に反映させることができるようになります。
例えば 下図はあるSF小説「○○」の売れ行きをすべての書店・通販サイトから調べる方法を示しています。
具体的な目的は、ある1週間のSF小説「○○」の購入率を調べることです。この場合の購入率とは、1週間に購入されたすべてのSF小説関係書籍の冊数に占める「○○」の購入冊数の比率です。
しかし、SF小説関係の書籍を扱う書店や通販サイトすべて(母集団)を調べ、購入比率を算出できれば、それにこしたことはありませんが、これらの書店は非常に多く存在するため、すべて調べることは不可能です。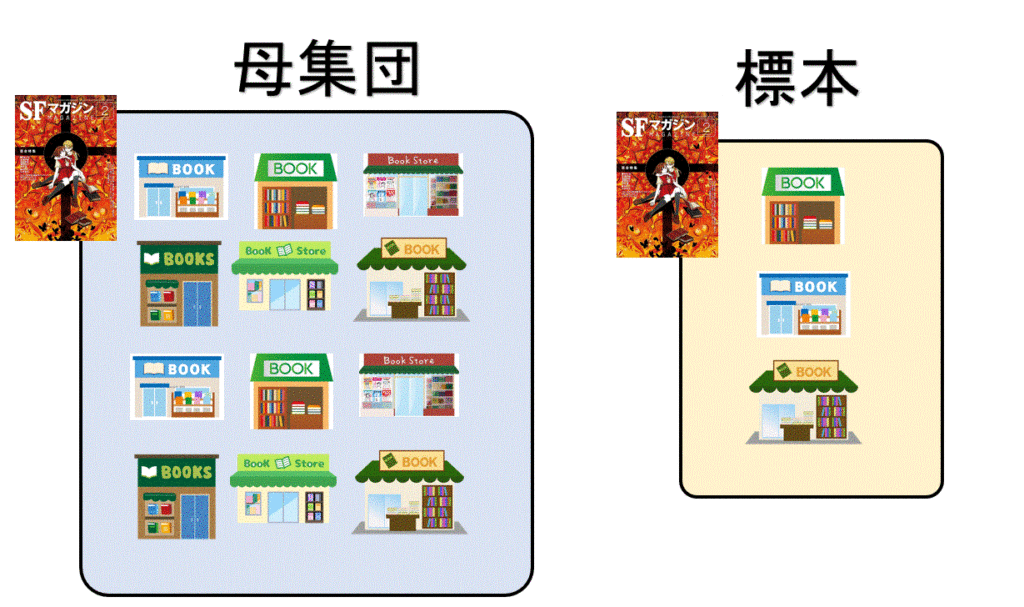
ランダムサンプリング(無作為抽出)
そこでランダムサンプリング(無作為抽出)という技術を使います。ランダムサンプリングとはある集団の中からランダム(無作為)にサンプル(標本)を抽出する手法です。
適当な数の書店・通販サイトを標本としてランダムに抽出し、1週間のSF小説関係書籍と「○○」の販売冊数を調べ、購入率を計算します。
調査対象がランダムに抽出されているので調査の結果得られる販売額や販売冊数のデータについても、ランダムであること、つまり、ランダムネスの仮定が成立します。
その結果、標本(データ)から計算された販売率は、母集団全体を調べたときにわかる真の販売率とほぼ同じ数値し(推定値)になると期待できます。
ビッグデータの問題点
ビッグデータは、絶えずデータが作成・収集・蓄積されるので、時間の変化に伴って売れ行きの変化を把握できるという利点があります。
しかし、問題がないわけではありません、とくに問題なのは、調査データの場合とは逆に、ビッグデータにはバイアス(偏り)があり、データのランダムネスを仮定することが難しいことです。
SF小説「○○」の売れ行きの事例で述べたビッグデータの場合、ある特定の通販サイトを通じて同書の購入情報を収集しているので、そこから算出された購入率は1つの通販サイトの実績を示すものでしかありません。
従って、全体の売れ行きを示す推定値として見なすことが難しく、確率の尺度で推定値の確からしさを評価することもできません。つまり、母集団を代表する購入率にはなりません。
データクレンジング(data cleansing)
ビッグデータを活用するに当たり、目的に合ったデータの抽出を行う必要があります。
ビッグデータには非常に多くの情報が含まれているため目的に合わないデータも存在しておりあらかじめ目的に合ったデータの抽出を行うこと(データクレンジング)でより高い精度の分析が可能になります。
しかし恣意的な意図が含まれるとデータが捏造される恐れが発生します。
データの標準化
ビッグデータを有効活用するには、社内全体でデータ整備を行う必要があります。部署ごとに異なるデータを扱っていると、企業全体でのデータ活用が進めにくくなります。社内全体で、同じデータを共有し、一元的な管理を行うことで、マーケティング対策が立てやすくなります。
データーの尺度別 分類
TV、新聞、インターネットが報道する情報には数値データー及びグラフで経済、社会、世界の様々な情報を日々、発信している。
データ(統計資料)&グラフは物事の推論の基礎となったり,判断のもとになるもので次のようないくつかの共通の性質がある。
1)ある調査や実験・観察の結果を表す情報の表現(数値や分類項目など),またはそれらから作成されたものである。
2)得られたデータ(統計資料)&グラフには測定誤差、サンプルリング誤差等の不確実性がともなう。
3)データ(統計資料)&グラフの背後には恣意的な操作、主観的な意思が入り、客観的なデーターは存在しない。
数値で表されるデータは、大きく4種類に分類することができます。
名義尺度、順序尺度、間隔尺度、比率尺度の4つです。
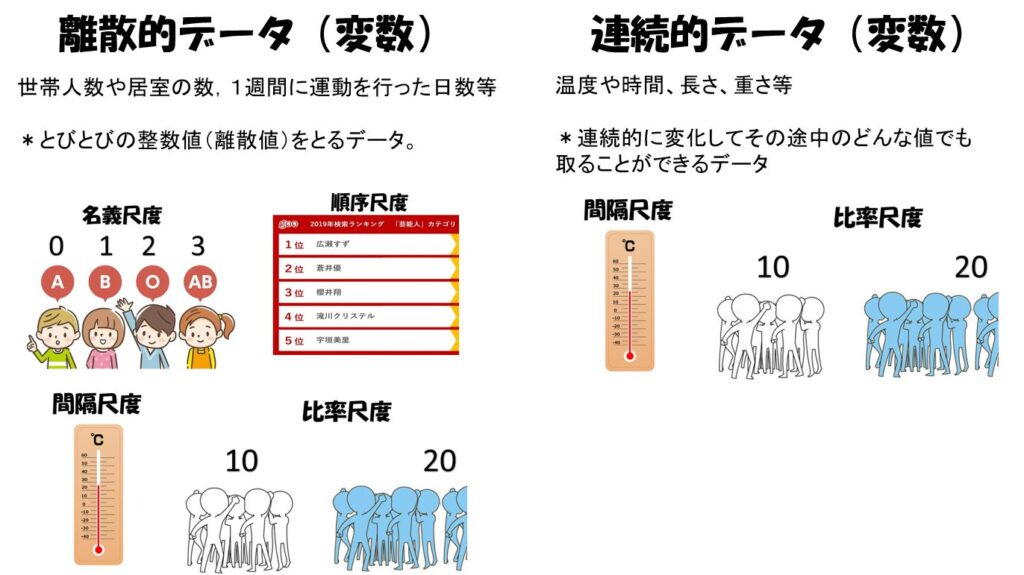
名義尺度の定義
値が等しいか等しくないかだけに意味がある数値を、名義尺度(nominal scale)と呼びます、つまり、対象を区別するためにだけ異なる値を付けている場合です。値の順序とか大小関係は意味がありません。
具体的には下記のようなアンケートの質問があります。
「あなたが一番好きな科目は何ですか? 1.国語 2.算数 3.理科 4.社会」
科目に付けられた1,2,3, 4,値の順序には特に意味がありませんから、これらの値は名義尺度になります。
又、血液型でA型・B型・O型・AB型をそれぞれ0・1・2・3と数値に対応させたものも名義尺度です。 これらの変数の平均値を求めてもまったく意味がありません。
順序尺度の定義
小さい順とか大きい順とか、値に大小関係の順序がついている数値を、順序尺度(ordinal scale)と呼びます。売り上げの順位や成績の5段階評価など、順序関係を持ちますが、値同士の差に意味はありません。
ランキング(ranking)における順位は順序尺度です。
例えばヒットチャートのランキング、テニスやゴルフの選手のランキング、幸福度の国別ランキング、世界の大学ランキング等です。
順位尺度で注意したいことは隣り合う値の間隔(差)は一定ではありません、よって順位尺度の平均値は厳密には正しくありません。
間隔尺度の定義
順序尺度では隣り合う値の間隔が一定ではありませんでした。これが一定である尺度を、間隔尺度(interval scale)と呼びます。値が等間隔で並んでいる尺度です、西暦、摂氏温度が該当します。
摂氏温度は1気圧で水の凝固点を0℃、沸点を100℃としてその間を100等分したものであり各値の間隔だけが意味を持っているので間隔尺度で測定された変数です。
間隔尺度では、比率(~倍)や割合(~%)を考えることがでぎません。
30℃は20°Cの1.5倍熱いとは言えません。
比率尺度の定義
間隔尺度では意味がなかった比率や割合が意味をもつ数値を、比率尺度(ratio scale)と呼びます。
時間、長さ、重さ(質量)などの基本的な物理量はすべて比率尺度です、30分は5分の6倍だなどと言えます。
又、金額、利率、人数・個数など、いわゆる普通のアナログ量は比率尺度です、年利0.4%なら、年利0.2%に比べて2倍の利子がつきます。
比率尺度は、0(ゼロ)が絶対的な原点として存在することが特徴です。0からどれだけ離れているかで、比率・倍率や割合を比べられるからです。
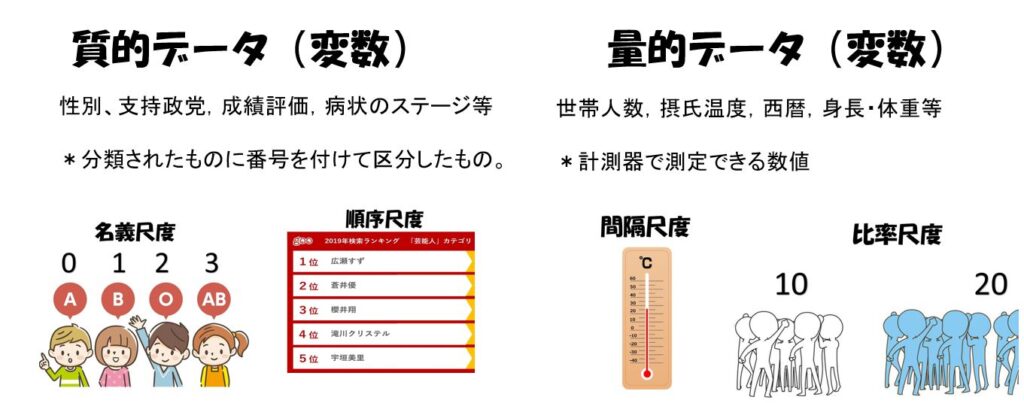
質的データと量的データ
名義尺度と順序尺度を質的データ(qualitative data)、間隔尺度と比率尺度を量的データ(quantitative data)と呼ぶことがあります。
質的データ⇒名義尺度または順序尺度
量的データ⇒間隔尺度または比例尺度(比尺度)
質的データは,性別や支持政党,住居の建築時期や学校の成績評価,病状のステージなどのように,いくつかに分類されたもの(それぞれをカテゴリという)の中から1つのカテゴリを取るようなデーターである。
量的データは,世帯人数,摂氏温度,西暦,身長・体重や距離などのように数値で与えられるような変数である。
離散的データと連続データ
上記の分類とは別に,量データーには離散データと連続データという分類もある。離散データ(discrete data)は,たとえば世帯人数や居室の数,1週間に運動を行った日数などのように,とびとびの整数値(離散値)をとるデータである。
これに対し連続的に変化して、その途中のどんな値でも取ることができるデータを連続データ(continuous data)と呼びます、例えば温度や時間、長さ、重さは連続データです。
名義尺度と順序尺度の数値は、離散的です。
間隔尺度と比率尺度には、離散的データと連続データがあります。
円で表した金額は、円未満の端下はありませんから、離散的データです、しかし、大きな金額になると、近似的に連続データと見なしてもよいようになります、これは人数や個数についても言えます。
以上で学んだ4つの尺度をまとめると下記の表になります。
| 質的か
量的か |
離散的か
連続か |
可能な演算 | ||||
| 等・不等 | 大小比較 | 差、平均 | 比率 | |||
| 名義尺度 | 質的 | 離散的 | 〇 | × | × | × |
| 順序尺度 | 質的 | 離散的 | 〇 | 〇 | × | × |
| 間隔尺度 | 質的 | 両方 | 〇 | 〇 | 〇 | × |
| 比率尺度 | 質的 | 両方 | 〇 | 〇 | 〇 | 〇 |
連続データ(変数)の誤差
誤差とは連続値をとる間隔尺度と比率尺度の数値には誤差がつきものです、通常、示された数値は、正確にそのとおりではなく、真の値はその近くにあります。
示された値と真の値との差を誤差(error)と呼びます。
誤差には、測定誤差、計算誤差、丸め誤差があります。
測定誤差
測定誤差(measurement error)というのは、物理量を測るときに生じる誤差です、ものさしで長さを測るとき、0.1mm単位で正確に測ることは無理です。
ストップウォッチで時間を測るとき、0.1秒単位まで正確に測るには訓練が必要です。又、体重計はふつう0.1kgの単位まで表示されますが、0.1㎏まで正確かどうかは疑問です。
長さも時間も体重も、連続的な値です、陸上短距離や水泳の公式迴技会では、記録が0.01秒の単位まで表示されます、ストップウォッチで測ったら10.1秒であったけれども、記録表示は10.07秒であったとします。
10.07杪が真の値だと仮定すると(本当はこれにも誤差があるはずです)、ストププウォッ
チで測った値は0.03秒の誤差を持っていまず。
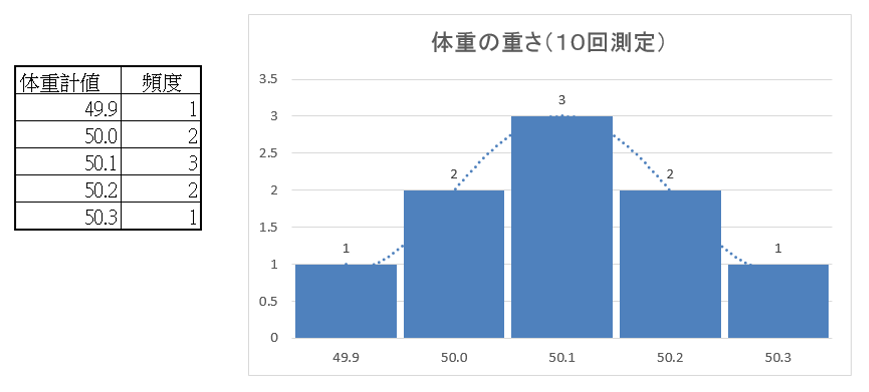
例を挙げると測定精度+0.1kgの体重計で体重を10回測定した時、測定結果が下記の表のようになり真の体重が50.1kgなのか50.2kgなのかわかりません。
真の値と測定値には必ず測定誤差があります、言い換えると“誤差をふくまない測定はありえません。真の値は理論的な数値であり頭で考えることはできますが数値として特定することはできません。
計算誤差
計算誤差(error in calculation)というのは、誤差のある数値を使って計算をした結果にともなう誤差です、そのなかで注意すべきなのは、桁落ちと丸め誤差です。
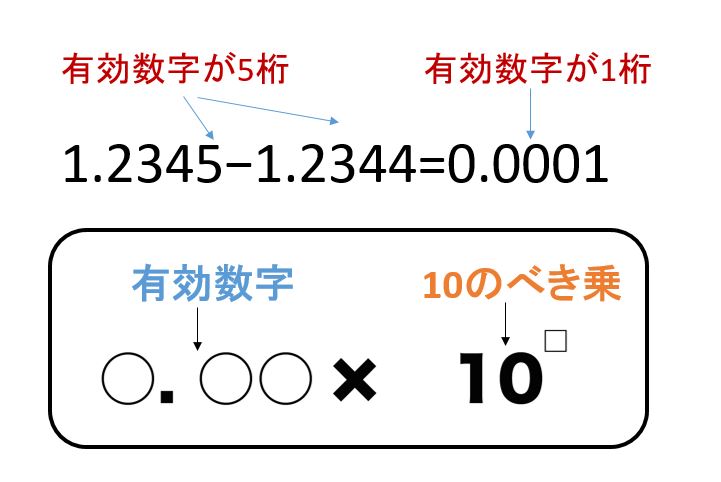
有効数字、有効桁数
1.26億人は、アラビア数字だけで書けば126,000,000となります。しかし、6つの0は位取りを表しているだけで、0という値を表してはいません。
値として意味があるのは、最初の3桁1, 2, 6だけです。これらを有効数字(significant figures)と言います。
また、有効数字の3桁を有効桁数と言います、6が有効数字や有効桁数に含まれると言っても6(600万)のところまで正確だという意味ではありません。次の桁を四捨五入して6としたのですから5である可能性もあります。
しかし、それでも6を有効数字、有効桁数に含めます。
測った長さが誤差も含めて16.3±0.2cmという場合には有効数字、有効桁数はさらに微妙です、1と6は正確ですが3は1~5のどれでもあり得えます。
しかし、有効数字は1と6だけであるとすると、四捨五入して16cmになる範囲がすべて入ってしまいます。
そこで、この場合、3も有効数字、有効桁数に含めることが多いようです。つまり、3の近辺だよということを表している有効数字です。
桁落ち
最近の日本の総人口(外国人を含む)を有効桁数5桁で見てみます。
2021年4月1日の概算値は1億2541万人です、 2020年4月1日の総人口は1億2593万人でしたから、1年で52万人減りました。
1 億2593万人も1億2541万人も有効桁数5桁ですが、差の52万人は有効桁数が2桁しかありません。
近い値のあいだで差をとると、有効桁数が減ってしまう現象を桁落ち(cancellation of significant digits)と言います、手計算や電卓で計算していると気がつきますが、コンピューターで計算しているときには気づきにくいので、注意が必要です。
桁落ちの例
「1.2345−1.2344」
を計算したいが、答えは 0.0001 になってしまい、有効数字が5桁から1桁に減少する。
この 0.0001 を、強引に有効数字5桁のように表すと、1.0000×10−4 となりますが、小数点以下の4つの 0 は意味が無い 0 です。
丸め誤差
丸め誤差(rounding error)の例を挙げます、円周率πは3.14159…ですが、159…を四捨五入してしばしば3.14と近似されます、 3.14は-0.00159…という誤差をもつわけです。
このように、ある桁より下を四捨五入したり、切り上げ、切り捨てしたりして、桁数の少ない値で表示したときに生じる誤差を丸め誤差と言います。
人数とか個数のように離散的な値でも、大きくなると連続値に近いとみなすことができ、誤差が入ってきます、日本の人口は1.26億人とですがこれはぴったり126,000,000人というわけではないです。 1.26の次の桁を四捨五入して1.26億人と表示したのです。
丸め誤差の例
「0.1212121212を 0.12 とみなして計算する」
のように、桁数が多い小数を、途中で四捨五入したり、切り捨て・切り上げする場合。
誤差のある数値の表示
表示する数値にどれくらいの誤差が含まれているかを示すには、○○±△△という書きかたが用いられます。たとえば、上にあげた日本の人口の表示では26±0.005億人と書けます、あるいは、1億2600万±50万人と書いてもOKです。
これを見た人は1億2550万人から1億2650万人の間にあると理解します。測った長さが6.3cmでも0.2cmくらいの誤差はありそうだと思ったら、16.3±0.2cmと表示します。
2020年のアメリカ大統領選挙のように接戦の場合には、予想得票率をA候補49%±1.5%、B候補51%±1.5%のように誤差も表示すべきです。
誤差の表示のない場合に比べて、A候補が勝つ可能性もあることが明確になります、2つの数値が、区別する意味がないほど近いときには、「誤差の範囲内だ」と表現します。
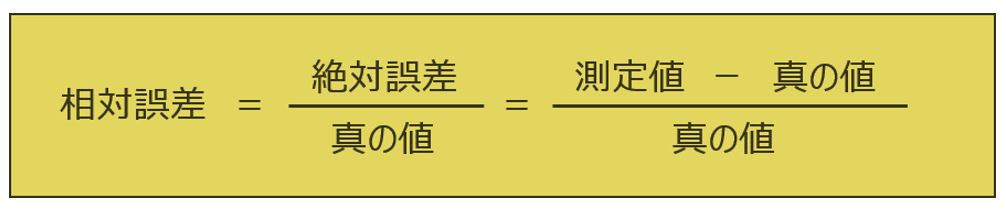
相対誤差(relative error)で表すこともあります、1mの誤差でも、それが真の値100m対するものか、10,000mに対するものかで正確さが違うからです(誤差/真の値)を相対誤差と言います。
(測定値ー理論値)÷理論値なので、例えば
(11−10)÷10=0.1
です。相対誤差は割合(比率)を表すものなので、単位をつけません。
北極から赤道までの経線に沿った長さは10,001 、966mです(国立天文台編:『理科年表2021』。 1mという長さは、1795年にフランスが、北極から赤道までの経線に沿った長さの1 / 10,000,000として決めました。
ほぼ0.02%の相対誤差であったわけです。
しかし、真の値がわからないことが多いので、そのときには(誤差/測定値など)で近似します、相対誤差にたいして、これまで述べてきた誤差は絶対誤差(absolute error)と呼ばれます。
基本的な数値の把握
日本、世界に関する基本的な数値は覚えておくと良いです、有効数字は1桁か2桁でOKです。
目の子算とは?
目の子勘定とは、一般的には、数量などを筆算など用いず、目で確かめながら計算することである。 建築業界では、目でざっと見ただけで寸法や数量を判断することを意味する。 「目の子」「目の子算」とも言われる。
事例1:1年はおよそ何秒ですか?
[解答]1分は60秒で、1時間は60分ですから、1時間は3,600秒になり、概算して4,000秒。
一日は24時間なので計算しやすくして25時間にして4000秒×25時間=10万秒。
一年は365日あるので10万秒×365ですから3,650万秒となります。
最終的に今まで多めに計算しているので3,500万秒が目の子算の解答です。
正確な数字は3,153.6万秒。
オーダーとは
オーダー(order)は 「数値の大きさの程度」という意味で、物理学や工学などの分野で、数値の大きさを大まかに表すために使います、簡単に言えば「単位」という意味です。
「10のオーダー」は「10の単位」つまり2桁「10~99程度」という意味になります。
10万秒と100万秒では「1桁オーダーが違う」と言います。
10万秒と1,000万秒では、オーダーが2桁違います、「目の子算では、真の値の1/3から3倍のあいだに収まればOKとする」のは、違いが土1/2オーダーの範囲に収まればいいという意味です。 1オーダー 以上、つまり桁が1つ以上違ってはいけません。
オーダーが違うと質が違う
経験則として、「オーダーが1つ違う(=大きさが1桁違う)と、量の違いが質の違いに変わる」と考えています。
例えばある仕事を1時間で仕上げてしまう人と10時間かかる人では単に能力の程度の差とは言えない影響が出ます、つまり簡単に言うと10時間かけてやる人は丁寧な仕事ができ、1時間しか時間がない人は雑な仕事になってしまいます、これが1日で終わるか、10日かかるかとなると、さらに大きな違いになります。
データの集約&要約
集めたデータを整形しデータシートを作成してもそれは単に数値の集まりなので、それだけで、何か新しいことや役に立ちそうなことがわかるわけではありません。データに「意味ある情報」を語らせることが必要です。
集計したデータの特徴を把握する方法としてグラフ化、平均値、標準偏差値等を求めて要約化があります。
データーを集計し、可視化する
「データに語らせる」方法として最初に行うべきことは、ともかく変数ごとにデータを集計して分布の特徴を見ることです。「分布の特徴を見る」ことが目的なので、グラフで可視化することも有効です。
そこで、量的データと質的データの場合に分けて、データの集計とグラフの役割を説明します。
量的データの場合
量的データ、とくに小数点を含む連続変数のデータの場合、そのまま集計しても、まず分布の特徴はわかりません。
下図は、このスーパーに買い物に来た顧客の、ある1日の買い物額を示したデータです。この図から、当日、買い物客が100人いたことはわかりますが、買い物額が1円単位の数値であるため、データを見ただけでは、買い物額分布の特徴がまったくつかめません。買い物客の購入品目の組み合わせは千差万別、買い物額も千差万別だからです。
・度数分布表を作成
先ほど述べたように、量的データ(特に連続変数のデータ)の場合、データをそのまま集計しても分布の特徴は把握できませんので度数分布表を作成します。
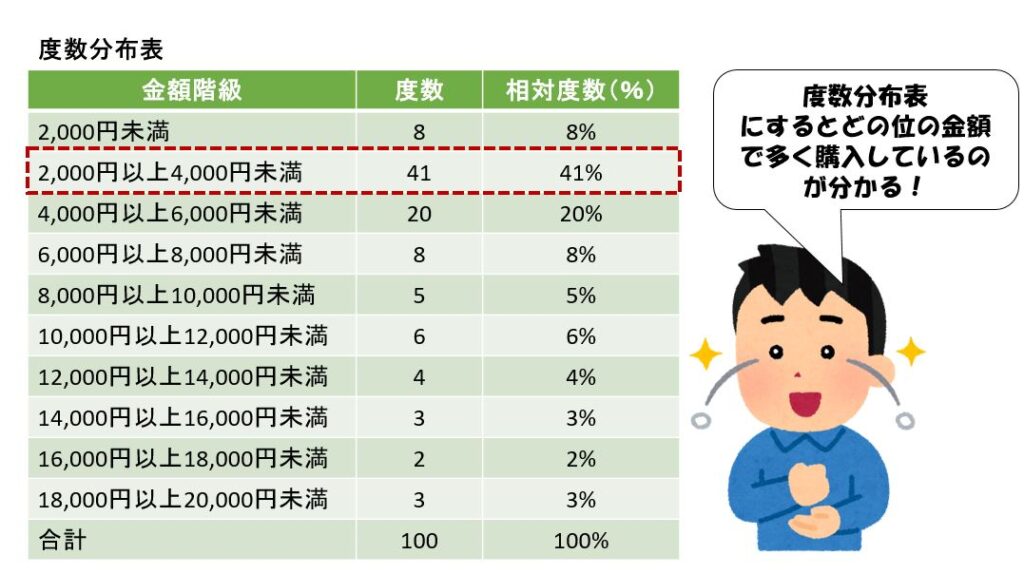
度数分布表とは、データを一定の区間(階級)にまとめて集計した表です。下図はこのスーパーに来た顧客の買い物額を一定の区間にまとめ、それに基づいて集計した度数分布表です。
なお、各金額の区間を階級と呼び、その階級の範囲内の金額で買い物をした顧客の人数を度数と呼びます。
量的データである金額を一定の範囲で区切り、該当する数を集計することによって買い物額分布が明らかとなり、さまざまな特徴を読み取ることができるようになります。
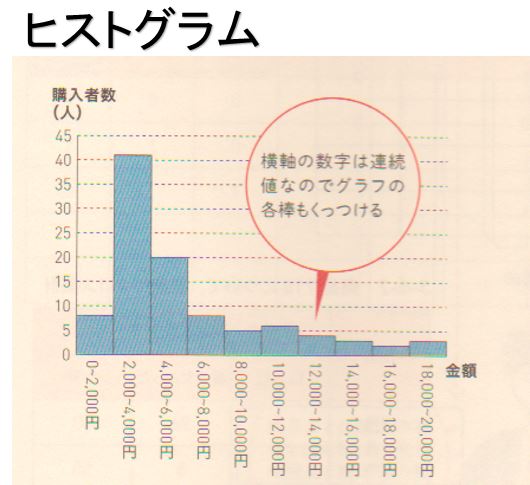
そして度数分布表を棒グラフにして可視化したものがヒストグラムです。
度数分布表及びヒストグラムの詳細は下記を参照してください。
質的データの場合
単純集計
量的データとは異なり、質的データは、尺度が名義的なものなので、直接データを集計(単純集計)することによって、各変数のデータ分布と特徴を把握できます。
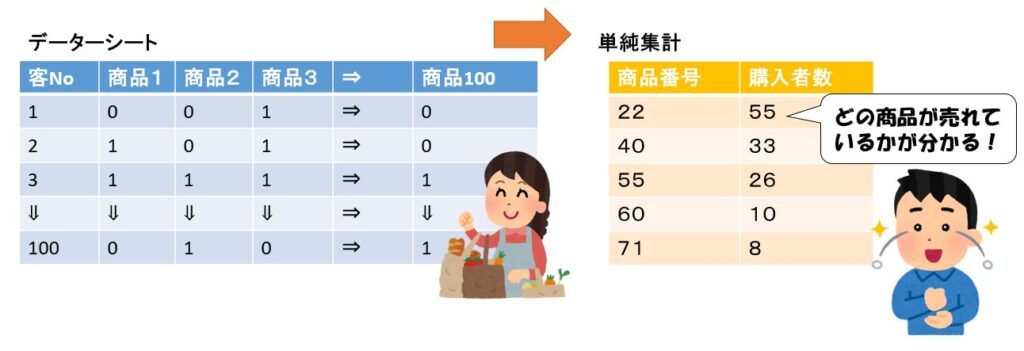
左下図はスーパーで顧客が購入した商品(購入した=1、購入しなかった=0)に限定して整形したデータシートと、最も多くの顧客が買ったベスト5品目を集計した結果です。
商品の数は無数にありますが、このようにデータを直接集計すると、すべての商品の購入者数を集計でき、右下図のように上位の商品の集計結果を示すこともできます。
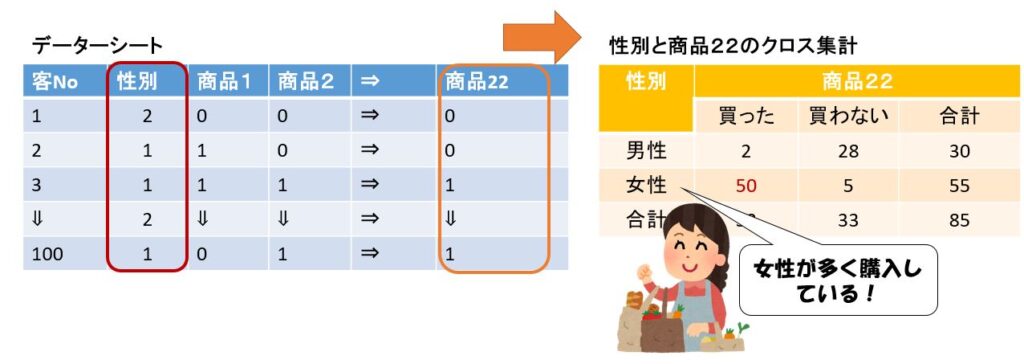
クロス集計
また、このデータシートは、それぞれの商品に関するカテゴリー変数から編成されてい
ますが、たとえば「性別」のようなカテゴリー変数も含まれていれば、この変数を組み合わ
せて、性別と商品購入の2つの変数を集計しデータ分布の特徴をつかむことも可能です。
このような2変数の集計をクロス集計と呼びます。
下図は商品の購入数に性別の変数を追加したデーターシートです、これを基にクロス集計を作成します。
データの表し方
間隔尺度や比率尺度のデータを示すときに、どのような表し方をしたら良いのか?
データの表し方には次のような選択肢があります。また、これらをいくつか組み合わせて表示する方法もあります。
(1)データ値そのもの
(2)ある基準値と比較した差(相対値)
(3)ある基準値と比較した比率
(4)(3)の相対値(相対比率)
(5)何かの単位あたりの値
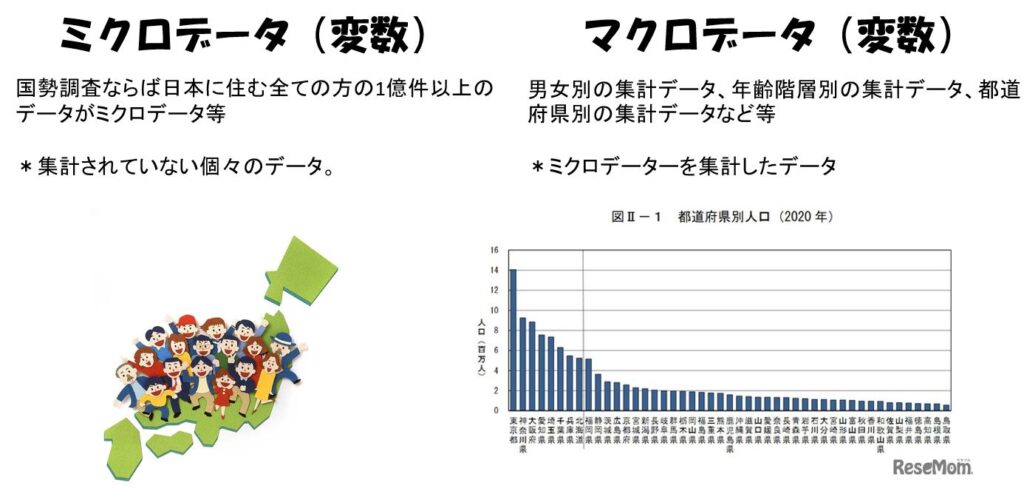
ミクロデータ(値そのもの)とは
ミクロデータとは集計されていない個々のデータという意味です。国勢調査ならば日本に住む全ての方の1億件以上のデータがミクロデータになります。
具体的な例で説明すると社会生活基本調査という調査は5年に一度、国民の生活時間を調査している統計です。
この場合、マクロデータは、男女別の集計データ、年齢階層別の集計データ、都道府県別の集計データなどで、これは統計局が公表しています。
都道府県別のマクロデータでは、47県、47個のデータということになりますが、実際には、社会生活基本調査では、全国で10歳以上の国民20万人の生活時間が調べられています。統計ミクロデータとしては、この20万人の国民のそれぞれのデータということになります。
個々のデータであるミクロデータからは量があり過ぎて有益な情報を得ることが難しいがこれを分析し、マクロデータとして抽出することにより貴重な情報を得ることが可能となる。
相対値とは
絶対値に意味がなく、相対値だけ意味があるデータもあります、地球温暖化で言われる地球全体の平均気温というのは、絶対値に意味がなく、産業革命前と比べて1.5℃上昇のような相対的な値だけが意味があります。
下図のように同じ2つのデータであっても比較する視点をどちらに合わせるかが変われば、値はプラスにもなりますしマイナスにもなります。
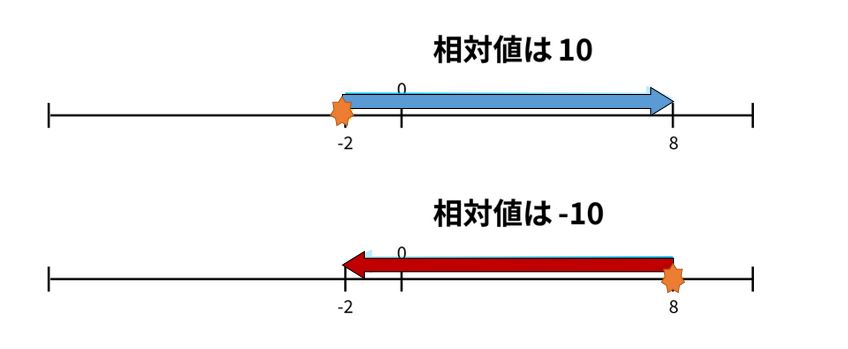 データの時間的変化を見るのに、ある時点の値を基準100として、それに対する相対的な比率で表したグラフはよく見かけます。
データの時間的変化を見るのに、ある時点の値を基準100として、それに対する相対的な比率で表したグラフはよく見かけます。
比率とは
比率については、「30%減った」と「30%に減った」とは間違いやすいので書く側・話す側も、読む側・聞く側も注意すべきです。
「30%減った」ですと、「基準値の70%になった」という意味です。
「30%に減った」ですと、文字どおり「基準値の30%になった」という意味です、テレビ等で「−30%」という表示をみかけますが注意が必要です。
比率で表されている値について、前回と比較する場合を考えます。
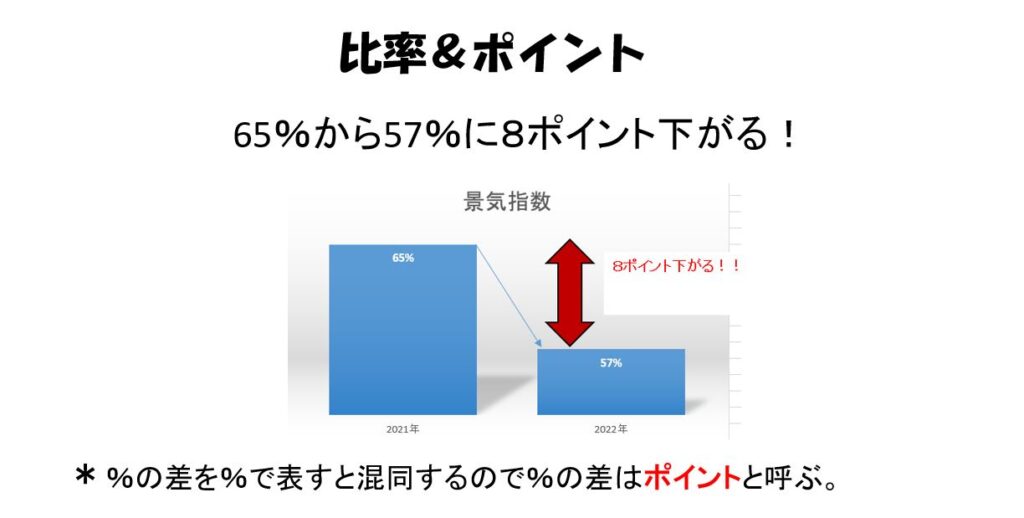
「景気が良いと答えた会社の割合は前回の65%から57%に8ポイント下がりました」という言いかたをします。
8%下がったと言うと、65%の8%、すなわち5.2%下がったと誤解されるおそれがあるからです、つまり、%の差を%で表すと混するので、%の差はポイントと呼んでいるのです。
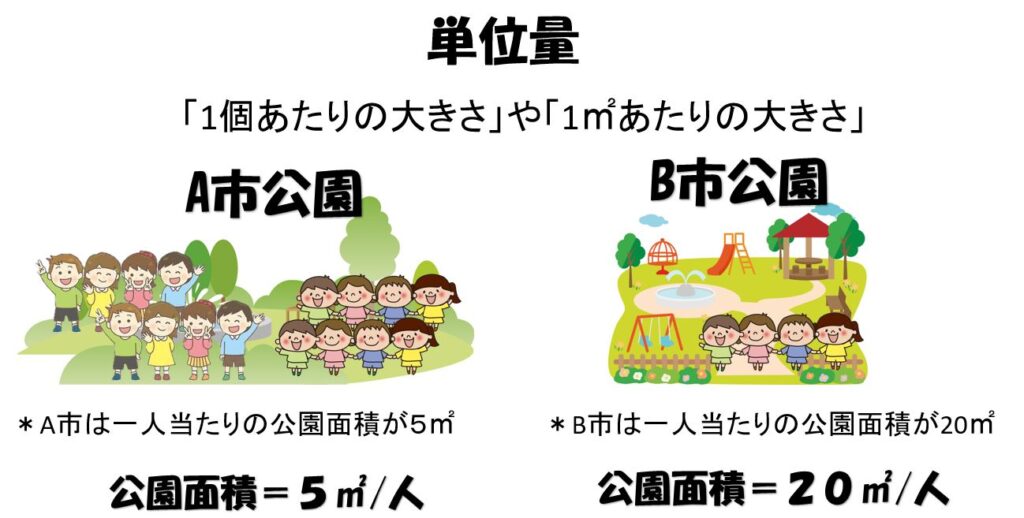
単位量(単位あたりの大きさ)とは
単位量(たんいりょう)とは、「1個あたりの大きさ」や「1㎡あたりの大きさ」を意味します。
例えば、ペットボトル500mlの水の質量が500gでした。水の1ml当たり(単位当たり)の水の質量は「500g÷500ml=1g/ml」のように計算できます。
例としてA,B市の公園面積を人口当たりの単位面積で比較する場合
A市は公園面積が50万㎡、人口が5万人
B市は公園面積が20万㎡、人口が1万人の場合
A市は一人当たりの公園面積が5㎡、B市は20㎡となり、B市の方が一人当たりの公園の面積が広くなります。
単純にA市は公園面積が50万㎡、B市は公園面積が20万㎡ だからA市の公園面積が広いとは言えません。
量的データの集約、要約
データを要約することによって母集団について有益な情報が得られるようになります。
例えば平均値、標準偏差、度数分布図等です。
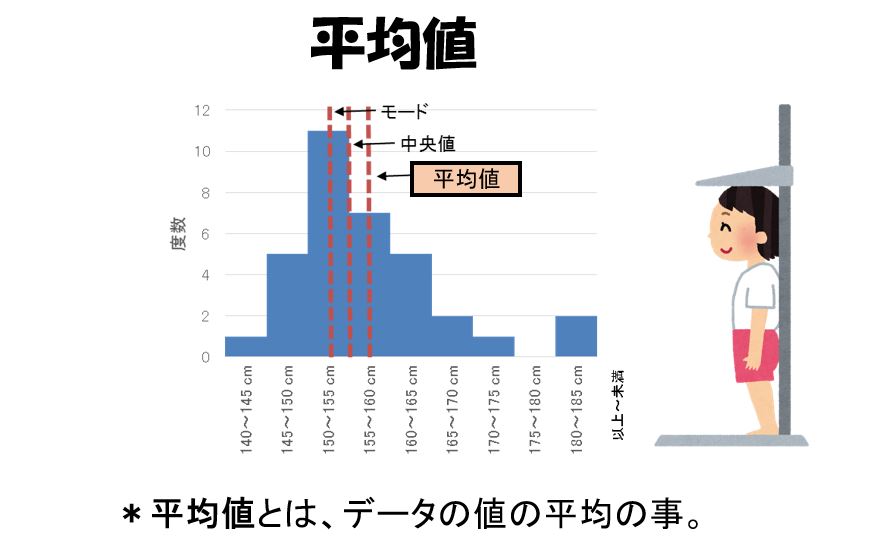
平均値とは
いくつかの数値がおおよそどのくらいの大きさであるかを1つの値で知りたい、示したい場合があります。
この目的のために、最もよく使われるのが平均(meanまたはaverange)です。平均値とも呼ばれます。
平均値の種類には相加平均、相乗平均(幾何平均)、調和平均があります。
相加平均は、最も代表的な平均です、一般的に平均値と呼んでいるのが相加平均です。
相乗平均は、成長率や上昇率(下落率)など、変化率の平均を求めるときに使用します。たとえば、ある地域の地価のデータから、対前年比の変化率を求め、過去5年間の年平均変化率を見たいような場合は、相加平均ではなく相乗平均を用いて算出します。
調和平均は、データの逆数の平均で、平均時速などを求めるときに使われます。
相加平均値(arithmetical mean)
与えられたいくつかの数値の合計を求め、それを数値の個数で割った値が平均です。
平均値(平均ともいう)は,広く用いられる位置の代表値である。変数xがx1,x2,x3…xnという値をとるとき,その平均値を
$$\bar{x}$$で表し,エックスバーと読む。
変数xの平均値は次の式で定義される。
$$\bar{x}={{観測値の合計} \over 観測値の個数}={{x1+x2+x3…+xn} \over n}=1/n {\displaystyle\sum_{i=1}^{n} xi} $$
ある会社の社員5人の月収が
265 280 292 294 311 (千円)
なら,このn = 5 人の月収の合計は1,442 (千円),平均値は288.4 (千円)となる。
これは,5人が収入を均等に分け合うときのひとりあたりの金額となる。このように,平均値は比較的意味をとらえやすく,計算も容易であることから,分布の中心の位置の代表値として用いれることが多い。
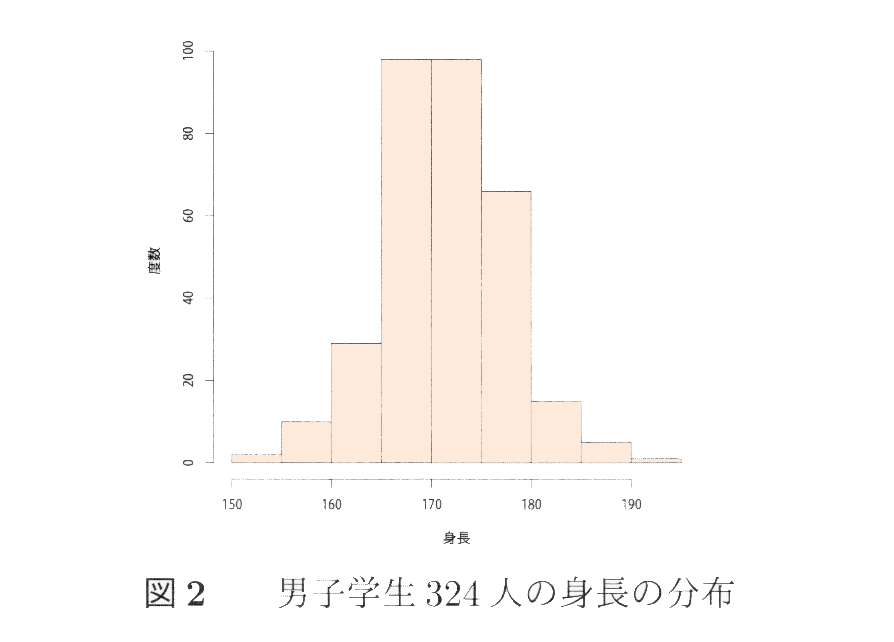
一般の場合には,身長などひとりあたりに分けるいう解釈ができない変数もある。しかし,図2に示す男子学生の身長データの分布のように山が1つでほぼ左右対称の場合には,平均値は最も度数が大きい分布の中心に近い。この意味で平均値は分布の中心的な位置の尺度とされる。
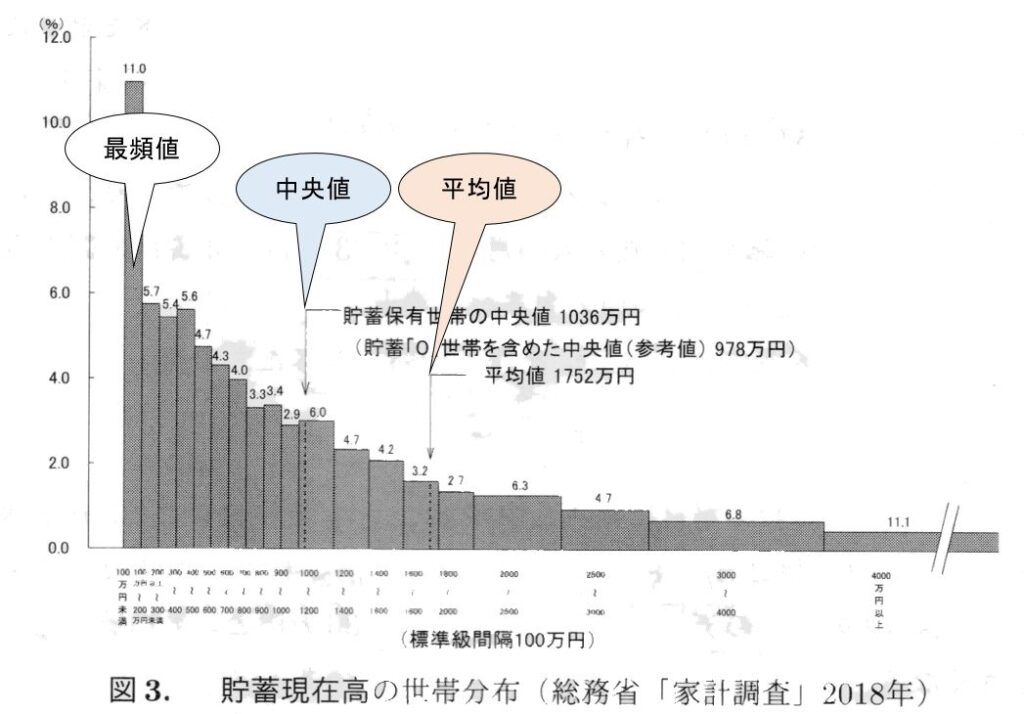
しかし,左右対称でない分布では,平均値を分布の中心的な位置と解釈しにくい場合もある。たとえば,図3に示した貯蓄現在高の分布は左右対称ではなく,右のすそが長い。
図3に示す貯蓄の分布は右のすそが長い。この図では平均値の1752万円の近くに多くの世帯があるとは言えないし,全世帯で貯蓄を再分配するわけでもないが,国全体としての平均的な豊かさを表す水準としては意味がある。
また,平均値は,外れ値の影響を強く受けることにも注意が必要である。
先程の社員5人に,月収が2600(千円)である管理職1人を加えた6つの観測値は
265 280 292 294 311 2600 (千円)
の平均値を計算すると673.7(千円)と大きく変化する。この例では,6人のうちに平均値に近い月収がある人はいない。
以上のように,右のすそが長い分布や外れ値が存在する分布の場合には平均値の解釈には注意が必要である。
又、偏差から簡単に平均値を求める方法もあります。
偏差から平均値を求める方法
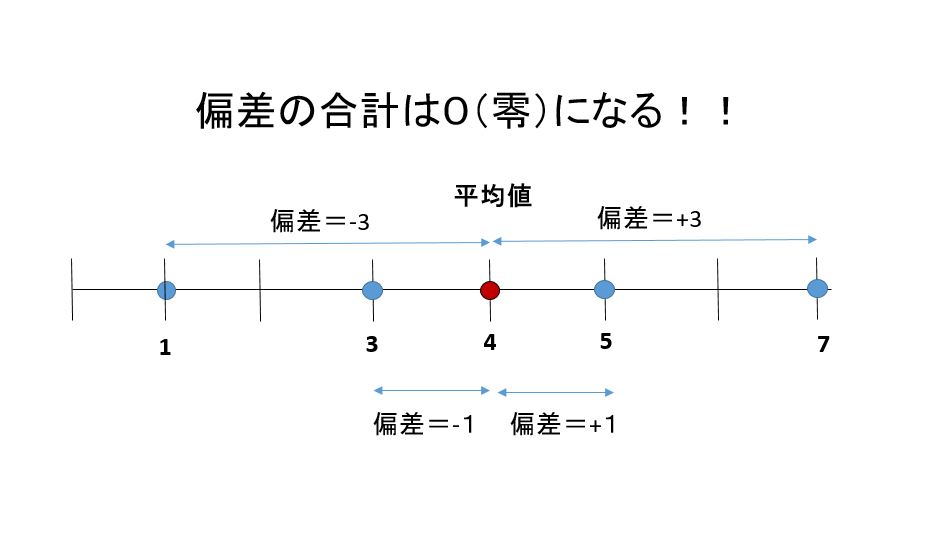
偏差(deviation)とは各データー値と平均値の差の事。
そして偏差の合計は0(零)になります、これを利用すると簡単に平均値が算出できます。
1,3,5,7の平均値は下記の図から4ですと算出できます。
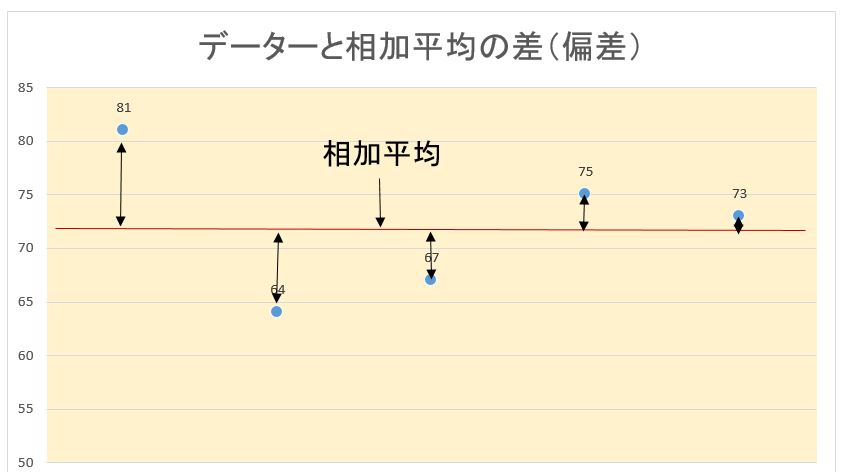
数値81, 64, 67, 75, 73の集まりのように、ある程度大きくてわりにかたまっているときには、次のようにして平均を計算することもできます。
数値をざっと見て、70前後に散らばっているなと思ったら、仮の平均を70とします。仮の偏差を求めると、11,-6, -3, 5, 3です。
これらの偏差の合計を求めます。3と-3は打ち消しますから、合計は11+5-6 = 10です。
10を数値の個数5で割って、2.0となります、2.0を仮の平均70に足すと、本当の平均72.0が求められます。
平均の欠点
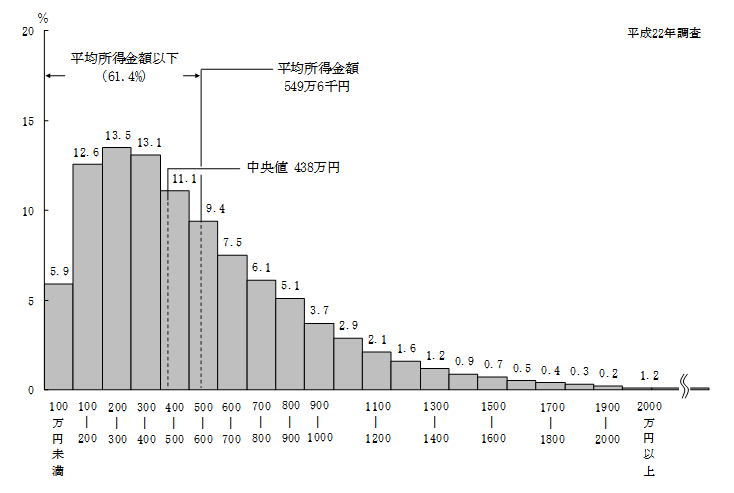
平成22年の世帯所得の平均値は549.6万円です、実は、所得のような高額所得者が少数ではあるデータに関しては、平均は実感より高めに出ます。
所得金額をいくつかの区間に分けて表示したものを下図に示しました、各区間の柱の高さは、所得がその区間にある世帯の割合です図の右裾のように、所得が1,000万円以上ある世帯が、しだいに少なくなってはいきますが、ある程度存在します。
平均はこれらの高額所得世帯に引っぱられて高めに出るわけです。
区間に分けて、各区間に入った数値の個数を柱の高さで示します。そういう図を度数分布またはヒストグラム(histogram)と言います、略して分布です。
上図は、数値の個数ではなく、全体の個数にたいする割合で示されていますから、正確には相対度数分布です。
相乗平均、幾何平均(geometric mean)
相乗平均とは,a>0,b>0のとき√ab,つまり,掛け合わせたときの平均です。経済学などに使われます。
a>0,b>0という条件がつくのは,ルートの中は正になるという約束があるためです。
相加平均と相乗平均の2種類の「平均」の大きさを比べると,常に,(相加平均)≧(相乗平均)となります。
a≠b のとき,(相加平均)>(相乗平均)・・・・・・①
a=bのとき,(相加平均)=(相乗平均)・・・・・・②
①と②を合わせて,(相加平均)≧(相乗平均)となります。
例えば,a = 3,b = 12 のとき,
相加平均は,(3+12)/2 = 7.5 相乗平均は,√(3×12)=√(6^2 ) = 6
したがって,7.5 > 6 となるので,①の(相加平均)>(相乗平均)が成り立ちます。
又、a = 4,b = 4 のとき,
相加平均は,(4 + 4)/2 = 4 相乗平均は,√(4×4) = 4
したがって,4 = 4 となるので,②の(相加平均)=(相乗平均)が成り立ちます。
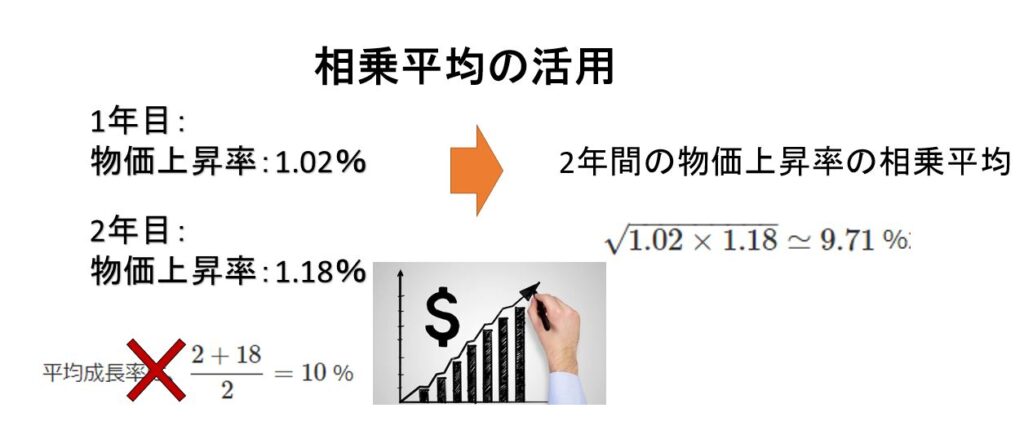
日常生活で「平均」と言うとたいてい相加平均です。しかし、相乗平均の方がふさわしい場面もあります。
例えば100 円だった物の価値が、1年目は 2 %上がった。2年目は 18 %上がった。この物の価値は年間平均何%上がったか?
この物の現在の価値は、100×1.02×1.18=120.36 円になります。
平均成長率は、(2%+18%)/2=10 %と言いたくなります。しかし、もし、100 円のものが2年とも 10 %で成長した場合。現在の価値は、100×1.1×1.1=121 円です。120.36 円とは微妙にずれています。これでは平均とは言えません。
正しくは、2年間の成長率の相乗平均:√1.02×1.18≃9.71 %が平均成長率になります,
実際、2年とも 9.71%で成長した場合、100×1.0971×1.0971≃120.36 円になります。
調和平均( harmonic mean)
調和平均は逆数の算術平均の逆数として定義され、例として、3つの数 1, 2, 4 がある場合の調和平均は次のようになる。
$$\frac{3}{\frac{1}{1}+\frac{1}{2}+\frac{1}{4}}=\frac{1}{\frac{1}{3}×(\frac{1}{1}+\frac{1}{2}+\frac{1}{4})}=\frac{12}{7}$$
で表します。
具体的事例としては
10kmの道を行きは平均時速 10km,帰りは平均時速5 kmで往復した時の平均時速は何kmといえるでしょうか?
[解答]単純に (10+5)÷2=7.5(km/h)とするのではなく,行き 10÷10=1(時間),10÷5=2(時間) となりますから,往復で3時間かかったことになります。よって,20÷3=6.7(km/h) となります。これを一つの式で書くと
$$平均時速=\frac{20}{\frac{10}{10}+\frac{10}{5}}=\frac{20}{1+2}=6.7(km/h) $$
これを上記の調和平均の式で求めると同様な答えになります。
$$\frac{2}{\frac{1}{10}+\frac{1}{5}}=\frac{1}{\frac{1}{2}×(\frac{1}{10}+\frac{1}{5})}=\frac{20}{3}=6.7(km/h)$$
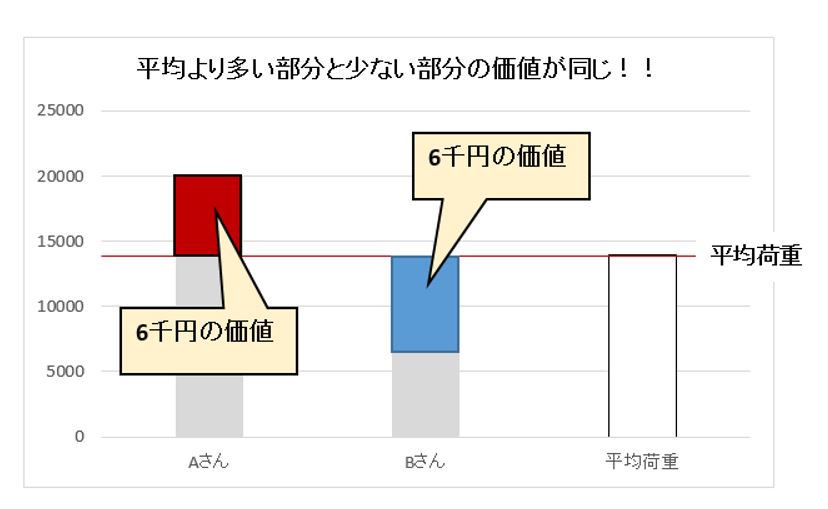
単純平均と加重平均
単純平均とは何個かの数をそのまま全部加えたものを、その個数で割って得た数。算術平均、相加平均とも呼びます。
一方、加重平均とは、データの「重み」を考慮して値の平均値を求める算出方法です。
価値が異なる場合はその価値を数値化して、掛け算してから平均を求めます。これを「重み」といいます。
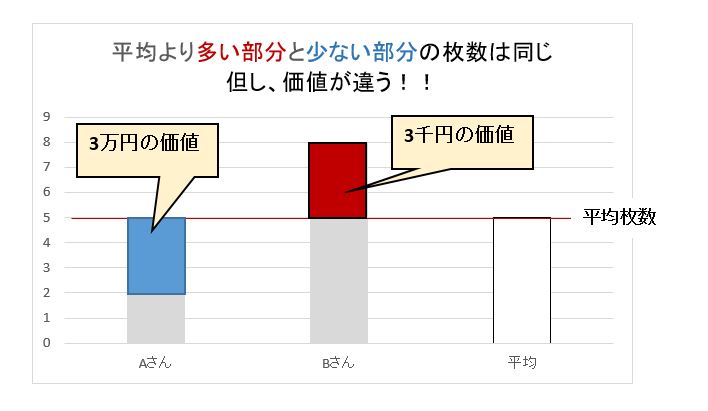
例えばAさんが一万円札で2枚、Bさんが千円札で8枚 所持したとします、2人の「枚数の平均」を求めると5枚です。
しかし「平均5枚」という答えは何の意味もありません。千円札と万札では1枚の価値が違います。種類が異なるもの同士で不足を補うことはできないので、単純に平均を求めてはいけません。
価値(種類)が違う場合はその価値(種類)を数値化して、掛け算してから平均を求めます。これを「重み」といいます。
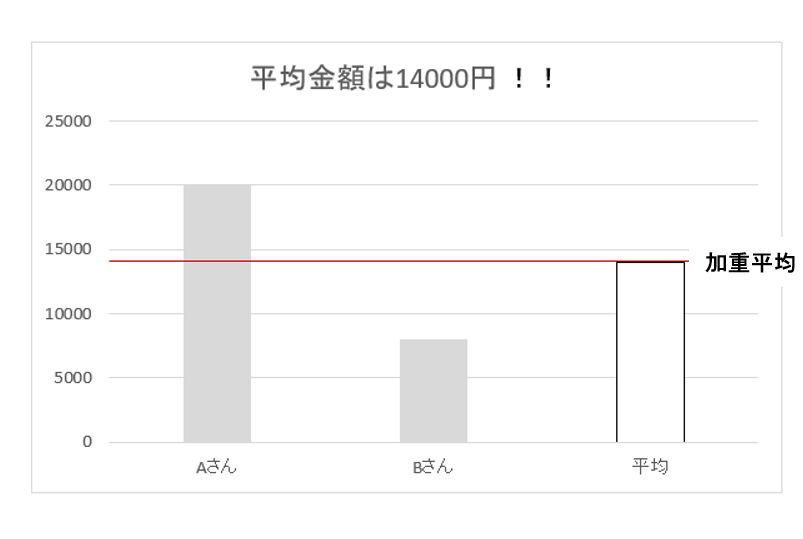
上記の例は下記のように計算します。
(10,000円×2枚+1,000円×8枚)/2=平均14、000円
人数や偏りなどの比率を考えない、単純な平均を「単純平均」または算術平均または相加平均といい、比率を考えた平均を「加重平均」といいます。
良く、間違いを起こしやすいのは平均値の平均を計算する時に重みの違う平均値を単純に足したり、さらにその平均を出すような計算です。
絶対に平均とを足して、更にその平均値を出してはダメです。
例としてある高校のクラスで英語の成績が男子は平均 70点(男子数:17人)、女子が平均 76点(女子数:13人)であった。
この時に価値、種類が違うグループの平均値を計算する時に単純に平均値を足して割っただけでは(70点+76点÷2)正しい計算結果がえられない、平均点数 73点ではない。
男子の成績の合計は70× 17=1190、女子の成績の合計は76 × 13 = 988です。成績の全合計は1190 + 988 =21780これを人数17 + 13 = 30で割って、全体の平均は2178 / 30 = 72.6です。
男子のほうが人数が多いので、全体の平均は( 70 + 76 ) / 2 = 73よりも小さくなるわけです。
このように人数が違うときは、人数を重みとして掛けて平均を求めなければなりません。これが加重平均(weighted average)です。
中央値とは
図4の中に書いてあるように平均所得金額549.6万円よりも少ない所得の世帯は、50%ではなく、61.4%あります。
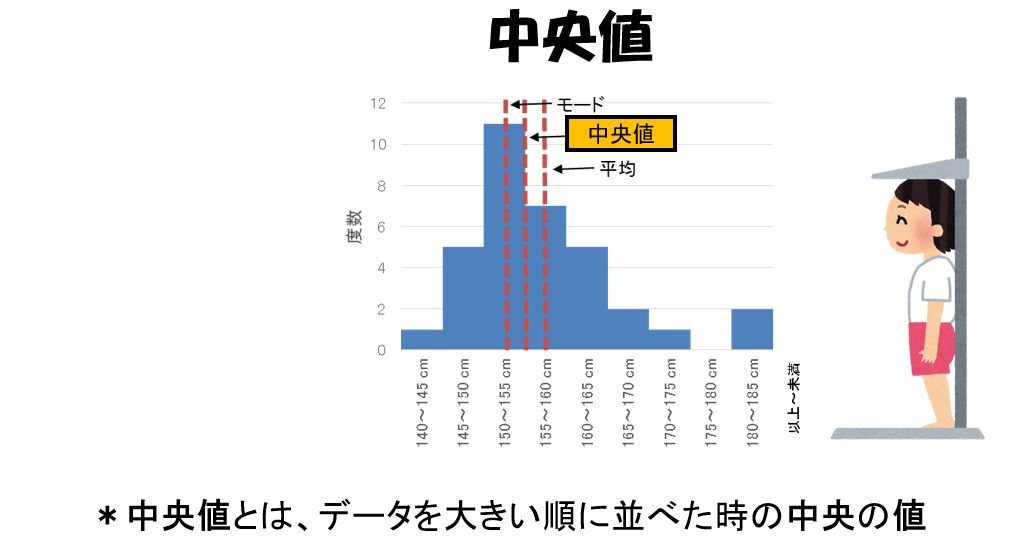
このような分布にたいして、全体の値の大きさを表す1つの値として平均よりも適切なのは、中央値です。中央値(median)は、各世帯の所得を大きい順に並べたときに、中央にくる値です。
中央値は、この場合438万円と記されています、中央値であれば、所得がそれより多い世帯も、それより少ない世帯も50%ずつですから、実感に近くなります。
ただし、中央値を求めるには、与えられた数値を大きい順に並べ替えしなければなりません。これは、平均を求める足し算と割り算よりもかなり手間がかかります、中央値よりも平均のほうがずっとよく使われるのは、そういう事情もあります。
中央値(median)は中位数、メジアン、メディアンとも呼ばれ、記号としはM、mが用いられる。
社員5人の月収については,真ん中は3番目の292(千円)であり,これが中央値である。管理職を加えた6人の月収なら,3番目と4番目の間を取って, (292+294)/2=293を中央値とする。
一般に,n個の観測値x1,‥‥,xnを小さい順に並べたものを
$$x1\text{≦}x2 \text{≦}…\text{≦}xn$$
とするときnが奇数の場合には真ん中のx((n+1)/2)を中央値としてnが偶数の場合にはn/2番目とn/2 + 1番目の平均値(x(n/2)十x(n/2+1)/2を中央値とする。
図4のデータでは,中央値は1036万円と,平均値よりかなり小さくなる。これは右のすそが長い分布の特徴である。
中央値は,ほとんど外れ値に影響されない。月収のn=5個の観測値に外れ値を加えたときの変化をみても,n=5のときは292(千円),外れ値を含めたときは293(千円)と,小さな変化しかない。このように,外れ値の有無にほとんど影響されないという点で,平均値とは大きく異なる性質をもっている。
最頻値とは
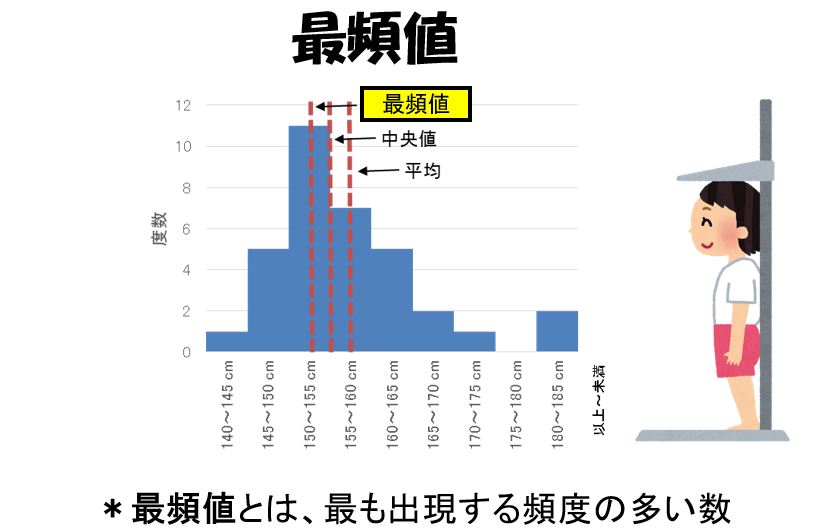
数値の分布を代表させるもう一つの値は、最頻値です、最頻値(mode)は値の大きさを図4のように幅が等しい区間に分けたとき、そこに入る数値の個数が最も多い区間の真ん中の値です。
図4の分布では、100~200、200~300、300~400万円の区間がほぼ等しい割合で最大になっています、その3つの区間の真ん中の250万円を最頻値とするのが適切です、つまり所得が50万円前後である世帯が最も多いことを示しています。
図3の貯蓄の分布のようにnが大きく,ヒストグラムがなめらかな場合には,最頻値はヒストグラムが最も高くなる値となる。
nがそれほど大きくない連続変数の場合には,複数の同じ値を取ることは少ないため,適当な級間隔を用いて作成した度数分布によって,ヒストグラムの高さが最も高い階級の代表値を最頻値とすることが多い。
しかし,nにくらべて級間隔が狭く,ヒストグラムの凹凸が激しいときには,最も度数の大きな階級が複数出現することがある。階級の幅を極端に小さくした場合には,ほとんどの階級で度数は0または1となってしまう。
階級の幅をある程度広く設定するなど,最頻値の解釈には注意が必要である。
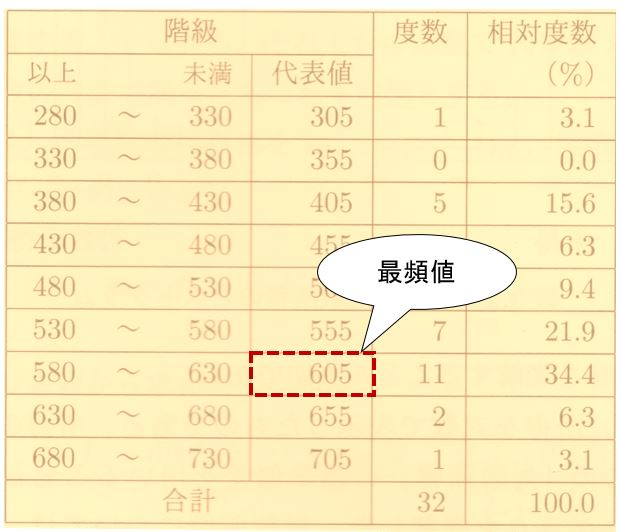
具体的な最頻値の求め方の事例として下記の度数分布表は,学校給食32日分のエネルギー量の階級を変えたものである。
この度数分布表で最も度数の大きい階級は580~630(kcal)であり,この階級の代表値605(kcal)が最頻値となる。
平均値、中央値、最頻値の違い
以上で3つの代表値について説明がデーターの分布が左右対称に近いひと山の分布であれば,平均値,中央値,最頻値はそれほど違わない。
これに対して右のすそが長い分布では,中央値は平均値より小さくなり、最頻値は中央値よりさらに小さくなる傾向がある。
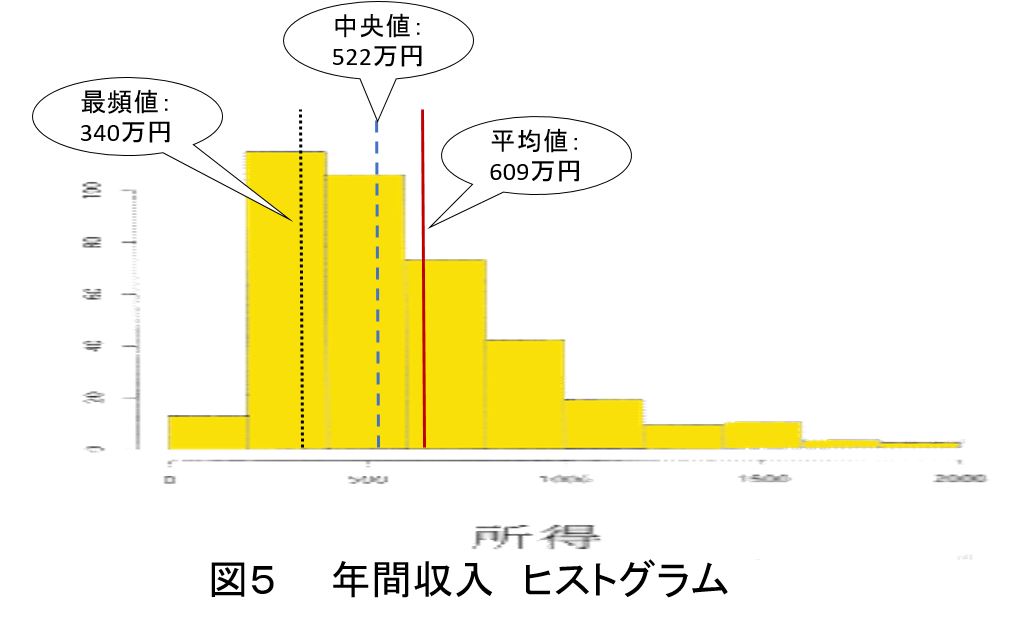
図5の左は年間収入のヒストグラム(対象世帯の擬似データ(n = 392)から作成したモノで右のすそが長いことから,平均値は609万円,中央値は522万円,最頻値は340万円となっている。対称でない分布については,3つの位置の代表値には違いがあり,これらの意味を理解することが大切である。
更にきわめて右のすそが長い分布である図3の貯蓄については平均値は1752万円であるのに対して,中央値は1036万円と,かなり異なった数値となる。最頻値はさらに小さく,ヒストグラムが最も高い100万円未満の階級の代表値は50万円となる。なお,この例では階級幅が一定でないため,標準級間隔100万円と記されているとおり,縦軸の単位は,ヒストグラムの面積が各階級の度数に比例するように記されている。
図では,平均貯蓄額より貯蓄額が少ない世帯の割合は67.6%となり,これらの世帯では「公表される貯蓄額は高すぎる」と感じる可能性がある,これに対して,中央値であれば,多くの世帯の実感に近いとされる。このような極端な例については,最頻値の意味を正確に理解して使う必要がある。
外れ値とデータクレンジング
データの集計などのとき、少数の数値がほかの数値から遠く離れていることがあります。それらの数値は何らかの事情で大きすぎる、あるいは小さすぎる値を取ったと考えら,そういう数値を外れ値 (outlier)と言います。
外れ値によって平均の算出が影響されるので、多くの場合、外れ値を除いて平均を求めるのが妥当です(分散や標準偏差、相関係数の計算でも、外れ値は除外します)。
平均は外れ値の影響を受けやすいのにたいし、中央値や最頻値は外れ値の影響をあまり受けません。
外れ値のうち、測定ミス・記入ミス等原因が分かっているものを「異常値」とよぶ場合があります。例えば、男性を「0」、女性を「1」で入力するアンケート調査に対して「2」が入力されていた場合、「2」が異常値となります。
但し、極端に小さい、大きい値であるからといってそれが異常値であるとは限りません、何か意味があって極端な値が出ている可能性もあり発生原因をよく考察する必要があります。
他のデータからみて極端に大きな値、または極端に小さな値が外れ値です。これは下記の方法で判断します。
・スミルノフ・グラブス検定をつかう方法
・四分位範囲(IQR)を利用した方法
があります。
たとえば、体重測定をした記録のなかに、455㎏と記録があったときにはどうでしょうか。おそらく体重データ入力する際に入力ミスしてしまったことが考えられますよね。“45.5”を“455”と入力しまったということです。
このように原因が特定できるもの、明らかに異常値だろうといえるものは、除外してしまって問題ありません。
データクレンジング(data cleansing)
データクレンジングとは、データベースなどに保存されているデータの中から、重複や誤記、表記の揺れなどを探し出し、削除や修正、正規化などを行ってデータの品質を高めること。
別名でデータクリーニング (data cleaning)とも呼ぶ。
データクレンジングを行うメリットはデータ分析の精度を高め、業務の生産性を上げひいては顧客からの信頼度を向上させます。
バラツキを要約、分散と標準偏差を求める
データ全体の変動を把握する計算方法で最もよく使われるのが分散とその平方根である標準偏差です。これらの方法は、個々のデータ間の違い(変動)を計ることから始めます。
分散σ²の求め方
例えば
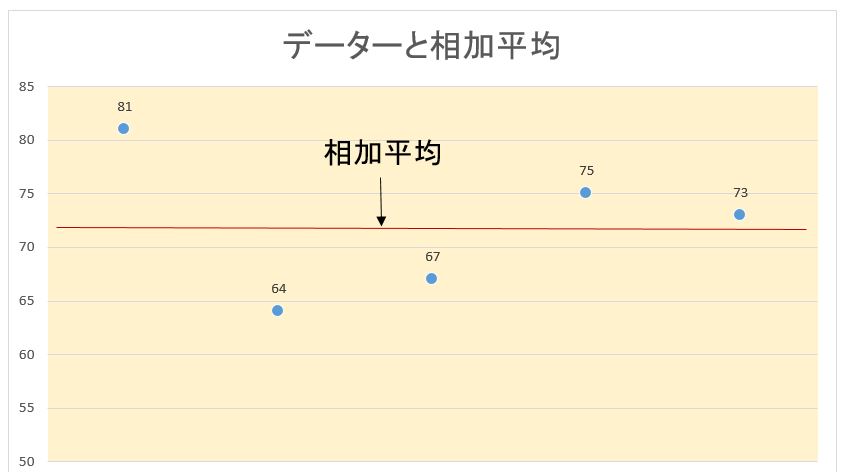
(a) グループ 81, 64, 67, 75, 73
と,集まり
(b)グループ 70, 76, 73, 67, 74
を考えます、どちらも平均が72ですが,平均のまわりのばらつきは(b)のほうが小さいことが見てとれます。
平均のまわりの数値のばらつきを測るために用いられる尺度が分散(variance)です、分散は
偏差=数値一平均
の2乗をすべての数値にたいして加えて,それを数値の個数で割った値です。
分散では「個々のデータと相加平均の差」の2乗を尺度としていることがわかります。2乗せずに「個々のデータと相加平均の差」を合計すると、0になってしまうからです。
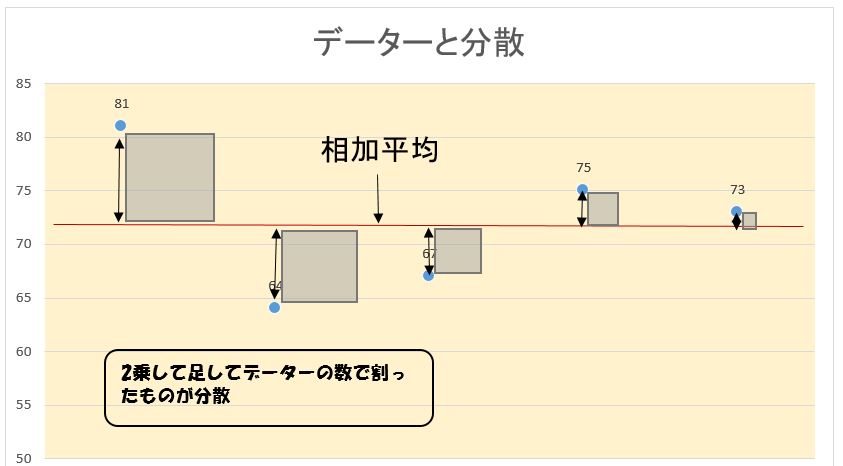
具体的に分散を求める計算過程を(a) グループ 81, 64, 67, 75, 73で説明します。
上記の分散の計算過程をグラフで表現すると下記のようになります。
分散は、ギリシャ文字、σ(シグマ)の2乗、すなわちσ²で表すのが慣習です。
そこで、平均をμとすると、分散は次の式で表されます。
$$σ2={(X1-μ)² + ( X2 -μ)²+‥‥+(Xn-μ)²}/n 式(1)$$
ある値を与えて、各数値とその値との差の2乗の和を考えま呪平均は、この差の2乗の和を最小にする値で丸そのときの最小値を数値の個数で割った値が分散です。
つまり、平均はある値のまわりの2乗で測ったばらつきを最小にする値になっています、これは、平均の意味として納得がいきます。
次の式が成りたちます。
$$分散=(数値の2乗の和)/個数一平均の2乗$$
つまり、
$$σ²=(X1²+X2²+‥+Xn²)/n - μ² 式(2)$$
標準偏差σの求め方
分散は,元の数値や平均と比べて,2乗の次元を持ちます、元の数値がm単位で測った長さだとすると,分散はm²の次元になります。
元の数値や平均と同じ軸の上で比較できるように分散σ2の平方根びを考えます、これを標準偏差(standard deviation)と呼びます。
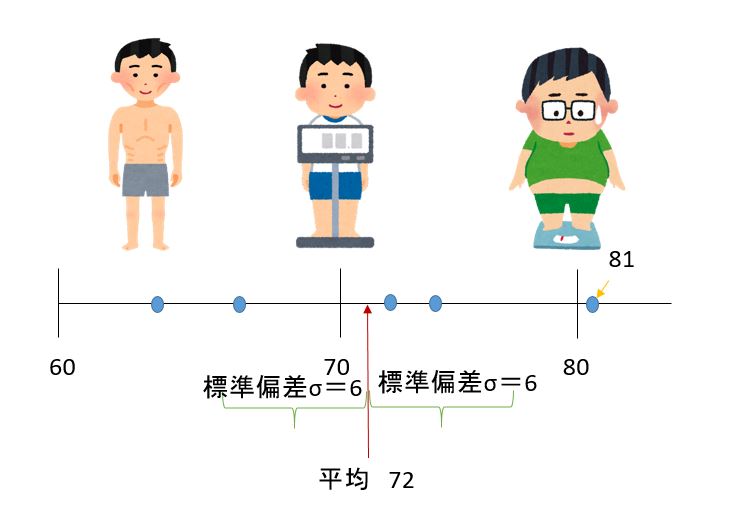
前に使った(a) 81, 64, 67, 75, 73の分散は36でしたから,標準偏差は6です。
(b) 70, 76, 73, 67, 74の分散は10でしたから,標準偏差は3.16です。
標準偏差がわかると,ある数値が平均から標準偏差の何倍離れているかを知ることができますたとえば, (a) 81, 64, 67, 75, 73の中の81は,偏差9(81-72)ですからすから,平均72から標準偏差6の1.5倍離れている事がわかります(下図)。
偏差値とは
偏差値は、受験生やその親にはなじみ深い数値です。
しかし、それが何を意味するのかとか、どのように計算されるのかについてはあまりよく知られていないようです。ここでは、それについて説明します。
例えば子どもが70点の答案を見せたとします、評価は?
まず、平均点が何点だったかが問題になります、試験が易しくて、みな良い点を取ったのかもしれませんし、その逆かもしれません。平均点が60点だったら喜べますが、平均点が80点だったらイマイチです。
平均点が60点だった仮定します。
次に知りたいのは、平均のまわりでどのくらいの広がりで得点がばらついているかです、つまり、標準偏差です。
標準偏差が15点だったら、70点は上から1/4くらいのところですが、標準偏差が5点だったら70点はたぶんクラスで1位です。
このように、試験の得点がわかっても、平均点や標準偏差がわからないとその得点が全体のなかでどのあたりにあるかはわかりません。そこで、平均点と標準偏差を知っているという前提で、それらに依存しないように、得点が全体のなかでどのくらいの位置にあるかを表示する値が偏差値です。
得点から偏差値を求めるには次のようにします。
まず、平均の影響を除くために、得点から平均を引きます、その差を標準偏差で割ります、これで、平均と標準偏差の影響をなくすことができましたが、わかりやすく使いやすいようにするために、少し加工します。
標準偏差で割った代わりに10倍します、その後、平均を引いた代わりに50を足します。
式で書くと次のようになります。
$$偏差値=(得点-平均)/標準偏差×10+50$$
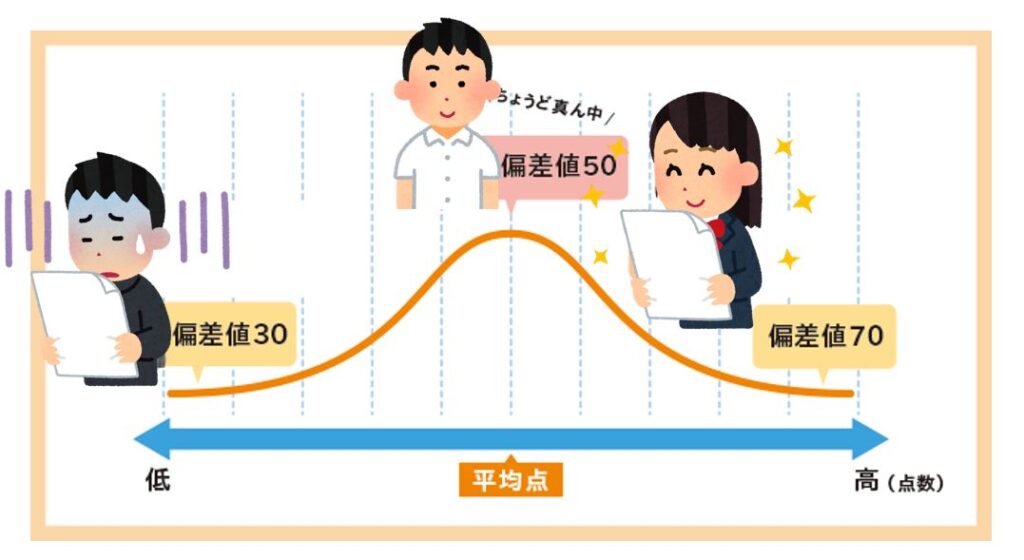
これで、元の得点分布の平均や標準偏差の値にかかわらず、偏差値は平均50、標準偏差10の分布になります。
つまり、平均を引いて後で50を足すことは平均を50に揃える操作、標準偏差で割って10を掛けることは、標準偏差を10に揃える操作です。
平均を50、標準偏差を10にすると、偏差値はだいたい20から80くらいの範囲の値になります100点満点の試験の得点よりやや狭い範囲ですが日常的になじみやすい値です。
得点が70点、平均が60点、標準偏差が15点という場合の偏差値を計算します。
$$偏差値=(70 - 60)/15×10+50≒57$$
変動係数の求め方
散らばりの程度を考える際に平均値の大きさを考慮しないと誤った解釈をする恐れがある。
たとえば,ある企業の従業者の年収を考えた際に
管理職の年収の平均値は2千万円,標準偏差は200万円
アルバイト・フリーターの年収の平均値は100万円,標準偏差は30万円
でした、このとき管理職の年収の標準偏差のほうがはるかに大きいが,解釈として「管理職の年収の散らばりはアルバイトより大きい」と考えるのは適切とはいえません。
このようなときは,標準偏差σを平均値µで割った
$$変動係数 CV =\frac{σ}{µ}$$
と呼ばれる変動係数を用います。(単位は無名数となり%で表すことが多い)。
この例では管理者の変動係数は200÷2000 = 0.1,すなわち10%。アルバイト・フリーターの変動係数は30÷100=0.3,すなわち約30%であり,平均値に対するばらつきの程度はアルバイト・フリーターの方が大きくなります。
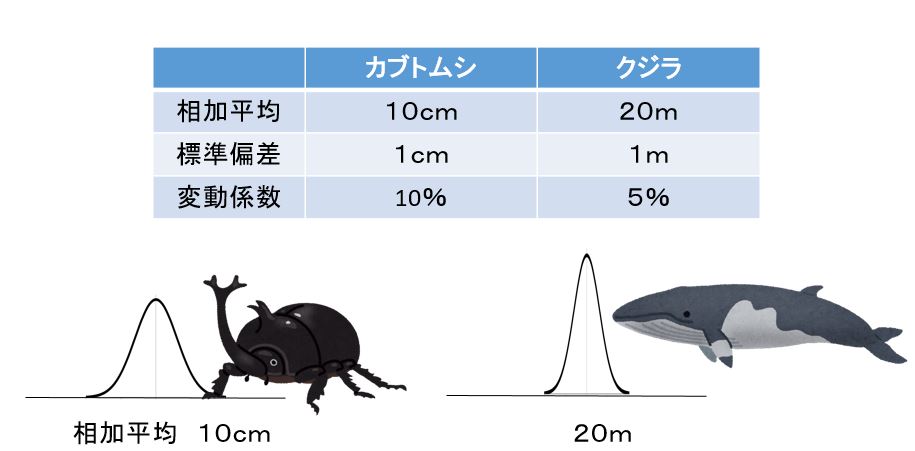
又、別な事例として、日本のカブトムシの大きさの標準偏差σが 1 cm であり、北極のクジラの大きさの標準偏差σが 1 m だったとします。
クジラの方が標準偏差にして 100 倍の大きさがある。 しかし、だからといってクジラの方がバラつきも大きいとは限らない。 元々、その生物がだいたいどれくらいの大きさなのかが分からなければ判断がつかない。
この時に変動係数を用いる。
カブトムシは平均 10 cm で標準偏差が 1 cm だとすると変動係数は 1 / 10 = 0.1 になる。
同様にクジラは平均 20m で標準偏差が 1 m なので変動係数は 1 / 20 = 0.05 。
変動係数は値が大きい方がバラつきが大きいことを表している。よってカブトムシの方がバラつきが大きい事を数値の上でも確かめることができる。
相関とは
相関(correlation)とは2種類の数値データの間で、一方が大きい時、他方も大きい傾向をもつか、あるいは他方は小さい傾向をもつか、それともどちらの傾向ももたないか、を表す用語です。
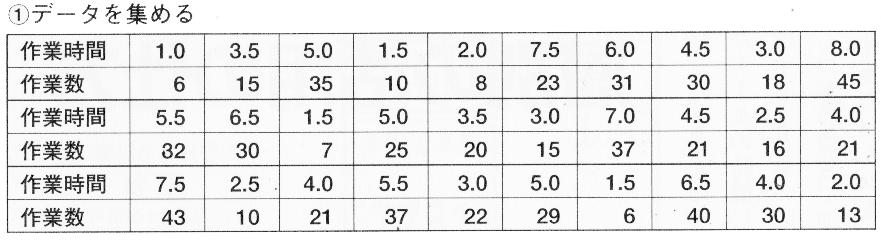
例えば作業数と作業時間の関係を調べるために下のような表を作成したとします。
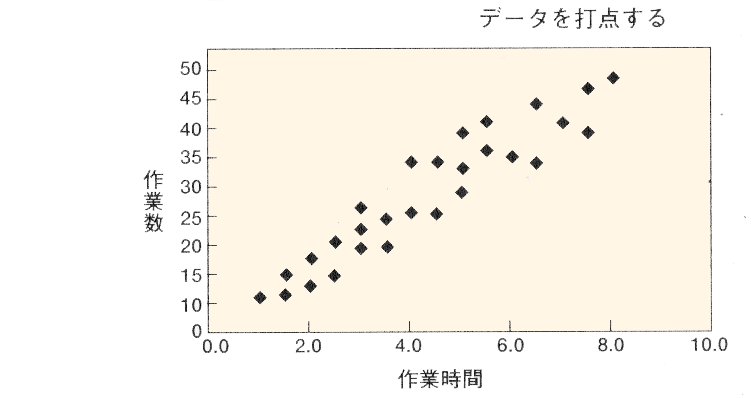
この表を目で関係性をわかりやすくで確認できるようにグラフにしたのが散布図です。
散布図は縦軸と横軸にそれぞれ2変数の尺度を置き、2変数のデーターポイントの交点をグラフにした図で二つのデーターの関係性を把握するのに適しています。
上の散布図を見ると全体的に点の集まりは右上がりになっています、つまり 作業数が増える程、作業時間が掛かる傾向があり、これを相関関係と呼んでおり、上の散布図の場合は正(プラス)の相関があると呼んでいます。
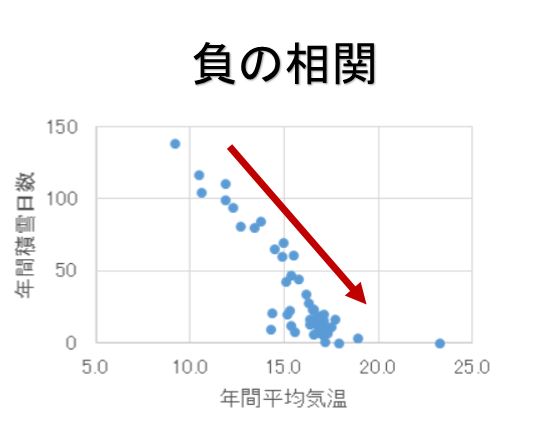
逆に下のような散布図の場合は負(-)の相関があると呼んでいます。
相関係数(correlation coefficient)
相関を1つの値で表すには、相関係数(correlation coefficient)が使われます。
相関係数の求め方については下記の記事を参照願いします。
関連記事:エクセル 散布図作成
散布図の相関係数 グラフの見方
相関係数による相関関係の強弱の判断基準は下記のとうりである。
0.8 ≦| r | → 強い相関あり
0.6 ≦| r | <0.8 → 相関あり
0.4 ≦| r | <0.6 → 弱い相関あり
| r |<0.4 → ほとんど相関なし
![[Tags] 1x1.trans エクセル 散布図作成](https://takuminotie.com/wp-content/uploads/2013/11/sanpu17.jpg)
![[Tags] 1x1.trans エクセル 散布図作成](https://takuminotie.com/wp-content/uploads/2013/11/sanpu18.jpg)
![[Tags] 1x1.trans エクセル 散布図作成](https://takuminotie.com/wp-content/uploads/2013/11/sanpu19.jpg)
相関と因果関係
ひんぱんに起こる間違いとして、強い相関を因果関係と勘違いしてしまうことがあります。
相関は2種類の数値データのあいだに一方が大きければ他方も大きい(または小さい)という関係があるというだけです。
極端な場合、強い相関は単なる偶然かもしれません。
それを一方から他方への因果関係であると報道、論文で論じることがありますので気をつけないといけません。
例を上げると
「アルコールを少し飲む人のほうが全然飲まない人よりも長生きする」と言われています』
しかし、考えてみれば逆に、「長生きする人はアルコールを全然飲まないよりも少しはアルコールを飲む傾向がある」とも言えます。
たとえば、重大な病気で医者からアルコールを止められている人もいるかもしれません。そこまで行かなくても、健康上の理由で自分からアルコールを控えている大もあるでしょう。そういう人たちは、そうでない大たちよりも寿命が短い傾向があります。
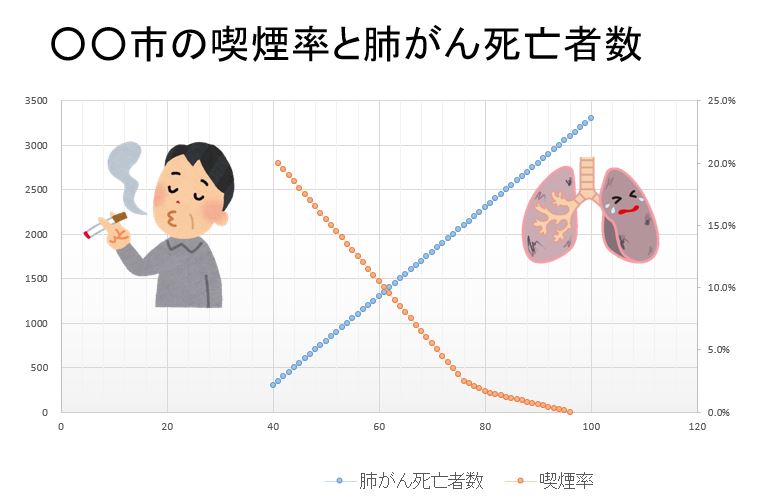
時間とともに変化する数値データを時系列データ(time series data)と呼びます、2種類の時系列データを時間軸上で表示したとき、値の増減の傾向がよく似ていれば、相関係数を計算するまでもなく、相関が強いと見なされます、この場合にも、よく因果関係と間違われます。
例えば男性の喫煙率は年と共に下がっていますが男性の肺がん死亡者数は増えています、負の強い相関があります。
よって『喫煙すると肺がんになる』は嘘でしょうか?
この場合、喫煙の習慣と肺がんの発生との間には何十年単位の時間の遅れがあります、又は肺がんを含めてガンによる死亡者数の増加は高齢者が増えていることに依ります。
因果関係の研究
次に,因果関係について考えてみる。2変数間に強い相関があることが因果関係を示すことにはなりません、因果関係を示すには何らかの関係が見られるだけでなく,2変数間に因果を判断できる根拠が必要になります。
たとえば、自動車の速度と停止距離の間には,速度を出せば出すほど,停止距離が長くなる、これは,運動エネルギーなどの物理的根拠からわかる因果関係である。
しかし一般に,因果関係があるのではないかと思われる2変数であっても,因果関係を明確に示すことは容易ではない。先に述べたように相関関係が強くても,必ずしもそれが2変数の因果関係を意味するわけではない。因果関係の有無を考察するには因果関係の研究が有用です。
統計の研究には実験研究と観察研究がある。
明確な根拠がない現象の因果関係の有無を調べるには,少なくとも実験研究を行わなくてはならない。
たとえば,あるドリンク剤の効果を調べるために,そのドリンク剤を飲んでいる人のみを対象に効果を調べても意味がない。
なぜならば体調がすぐれないのでそのドリンク剤を飲んでいる人が多い場合,効果がないという結果が導かれることがある。
このようなときには,対象者をドリンク剤を飲むグループ(Aグループと呼ぶ)と飲まないグループ(Bグループと呼ぶ)に分ける。
Aグループに属する対象者のみにある期間そのドリンク剤を飲んでもらった後に,ドリンク剤を飲んでいないBグループの対象者と比較する。それによって,Aグループの方がより良い結果を示したなら,そのドリンクは体に良いと推定される。
擬相関(見かけ上の相関)
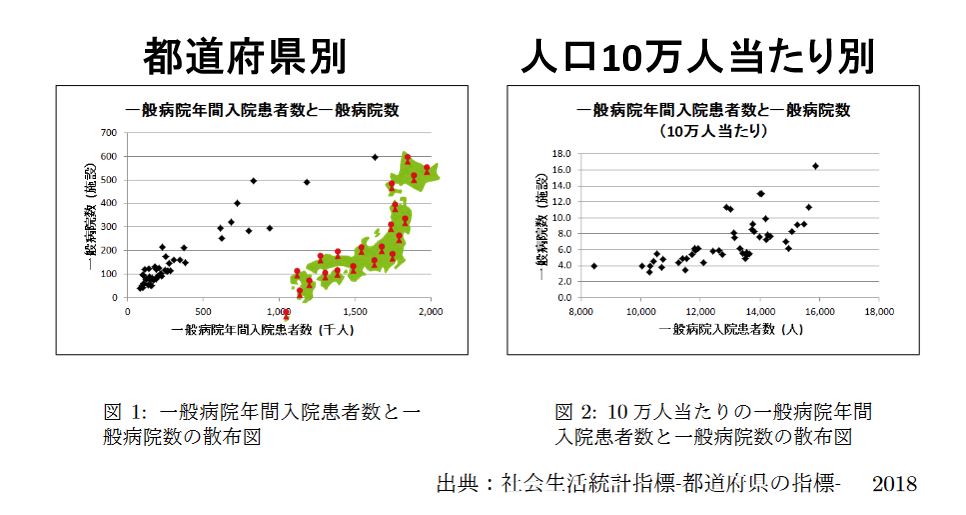
下の左図は2015年の都道府県別の一般病院年間入院患者数と一般病院数の散布図である。これら2変数の相関係数は0.95で,強い相関がある。
入院患者数が多いから病院数が多いと解釈することもできるし,逆に病院数が多いから入院患者数が多いと解釈することもできる。
都道府県の人口は大きく異なり,この影響で入院患者数と病院数の相関係数を大きくしている可能性がある。
そこで下の右図のように,人口10万人当たりの一般病院年間入院患者数と一般病院数を調べると,その相関係数は0.70となる。つまり,相関係数の値が小さくなり,人口の大きさの違いが影響していることが分かる。
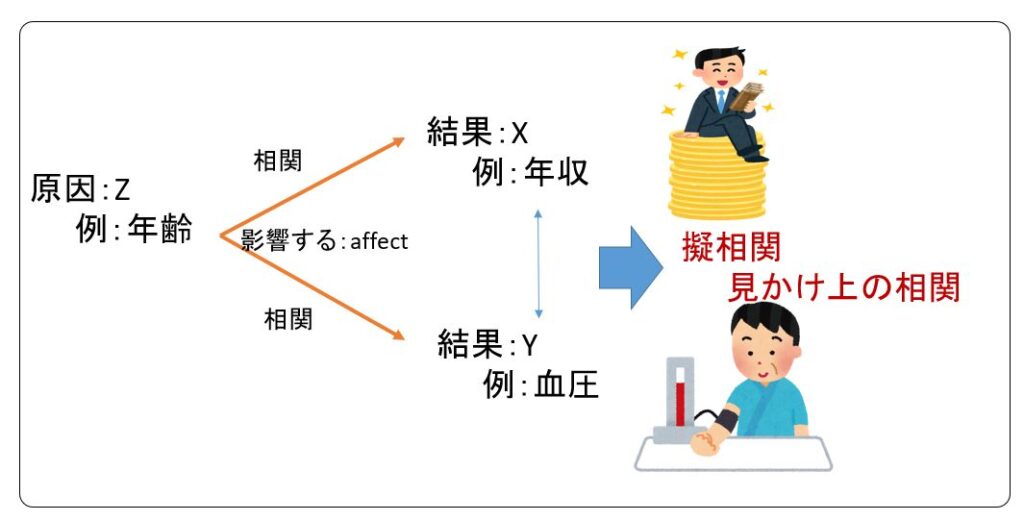
又、下図のように2変数 X,Y 両方に影響を与える第3の変数Zが存在したためにX,Yの間に相関関係がみられるという現象を擬相関(見かけ上の相関)という。
日ごろ「○○をすると××になる」というような文章を目にするが,十分な検証がなされていない場合,擬相関を述べていることがあるので,文章の内容を注意して理解しなければならない。
例えば一般的に年齢が上がると年収が上がり、血圧が高くなるがだからと言って血圧が上がると年収が上がるとは言えない。
データーの分類 多変量データ解析
多くの変数からなるデーターシートを使用して多次元データを総合的に分析するにはグラフ、1変数だけの分析では不十分です。
多くの変数を含む多次元データでは、さまざまな変数を組み合わせ、それらをまとめて分析すると、グラフや1変数を分析しただけでは見えなかったさまざまな特徴や傾向が見えてくることがあります。
そのような分析に用いるデータ解析の方法を多変量データ解析と呼びます。
多変量データ解析にはさまざまな手法がありますがデータを要約する場合とデータを要約する場合にわけられます。
データを要約する場合
データを要約する場合には、次のような手法があります。
| データ要約手法名 | 概要 |
| クラスター分析 | クラスター分析とは、異なるものが混ざりあっている集団の中から互いに似たものを集めて集落(クラスター)を作り、対象を分類するという方法の総称です。
例えば例えば、企業が保有している顧客リストを顧客の属性や関心によって分類すると、それぞれの顧客に対して適切なマーケティング施策を模索しやすくなります。 |
| 主成分分析 | 多次元データのもつ情報をできるだけ損わずに低次元空間に情報を縮約する多変数解析の一種です。
例えば、身長と体重(二次元のデータ)から肥満度を示すBMI(一次元のデータ)に変換するのは主成分分析の代表例です。 |
| 因子分析 | 主成分分析と同様の場面で使用する |
| コレスポンデンス分析 | 自社ブランドと競合ブランドのイメージを表で視覚的に把握する |
| 多次元尺度構成法 | コレスポンデンス分析と同様の場面で使用する |
特にクラスター分析は、アンケート調査の質問項目(カテゴリー)や回答者を回答の類似性から分類し場合に良く使用される手法です。
又、クラスター分析は大きく,最短距離法などの階層的手法 (hierarchical method) と,k-means法などの非階層的手法 (non-hierarchical method) に分けられますが,これらの基本的手法を紹介します。
クラスター分析、 クラスタリング (clustering)
クラスター分析は多くの変数から見たときに、それらをまとめて、似たパターンを示すデータポイントを分類するデータ解析の方法です。
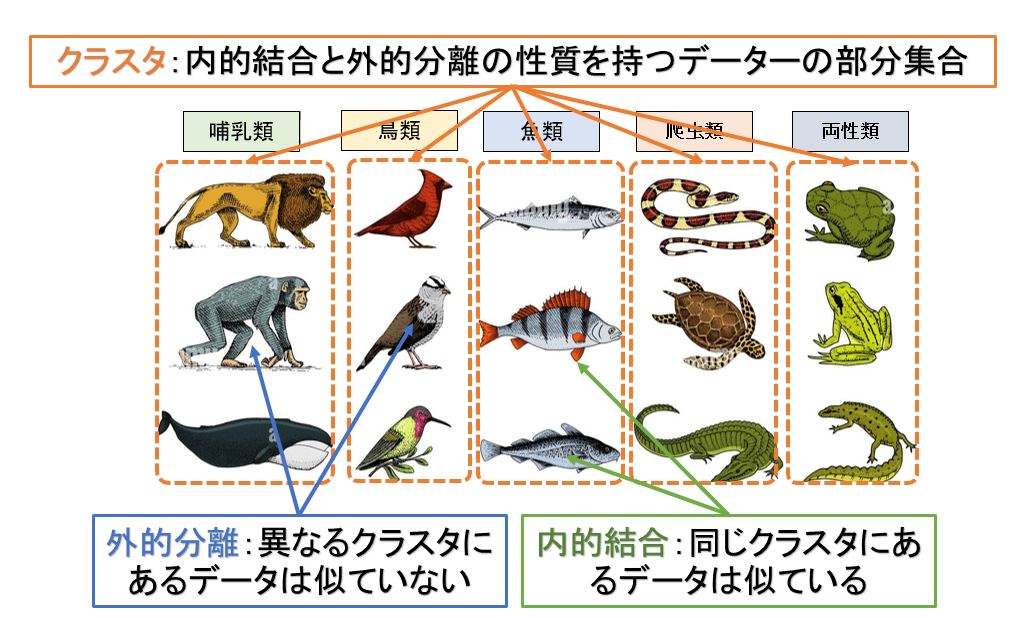
別名、クラスタリング (clustering) とも呼ばれ、分類対象の集合を,内的結合 (internal cohesion) と外的分離 (external isolation) が達成されるような部分集合に分割する、基本的なデータ解析手法です。
通常、私たちは物事を整理整頓する際には、機能、形状などの側面から似ているものを同じのところに集めて、片付ける。
例えば動物のクラスター分析は下図のようになる。
これと同様にデータについてもデータ構造の側面から似ている個体を同じのグループに仕分けることが必要である場合がある。
クラスタ分析と分類の違い
データサイエンスにおけるグループ分けの方法は、教師データがある分類と教師データがないにクラスタ分析に大別される。
ここで言う教師データとは、どの個体がどのグループに属するかが既知であるデータの事であり、グループの所属を示すデータは外的基準とも呼ばれている。
教師データがないグループ分けは、どの個体がどのグループに属するかに関する事前情報がないデータについて、グループ分けする方法で、外的基準がない分類法であり、この分類方法がクラスター分析である。
ここのクラスター (cluster) とは、花やブドウなどの房の意味で、クラスター分析とは、データの構造が似ている個体を同じの房(グループ)にまとめて、そうでないものを異なる房に集めるデータの処理方法である。
つまり、クラスタ分析(クラスタリング)と分類には大きな違いが存在し、それは、「グループ分けに明確な答えが存在するかどうか」です。
教師データ(基準、定義)を基にデータをグループ分けするのが「分類」であり、
教師データ(基準、定義)はなく、あくまででもデータを基にグループ分けするのが「クラスタリング」です。
クラスター分析には階層的クラスター分析と非階層的クラスター分析があり、下記にその概要を説明します。
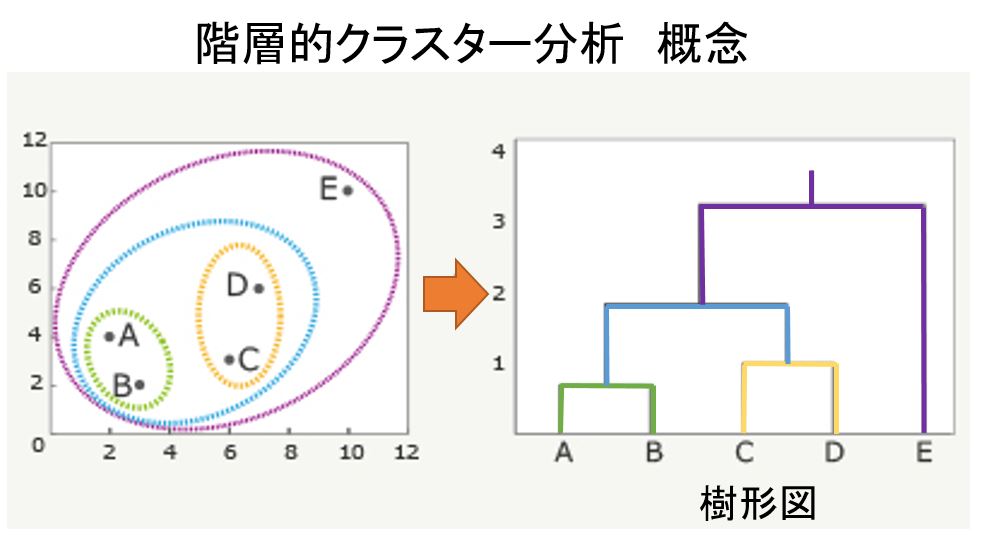
階層的クラスター分析とは
最も似ている組み合わせから順番に群(クラスター)にしていく方法で、途中過程が階層のように表せ、最終的に下図のような樹形図(デンドログラム)を作成します。
階層的クラスター分析に色々な方法があるが基本は次のようなステップを踏む。
Step1 距離 (あるいは類似度) を求める方法を選択し、個体間の距離 (類似度) を計算。
Step2 クラスター分析の方法 (最近隣法、最遠隣法など) を選択。
Step3 選択された方法のコーフェン(Cophenetic)行列を計算。
Step4 コーフェン行列に基づいて樹形図を作成。
Step5 樹形図の結果について検討を行う。
樹形図生成 手順
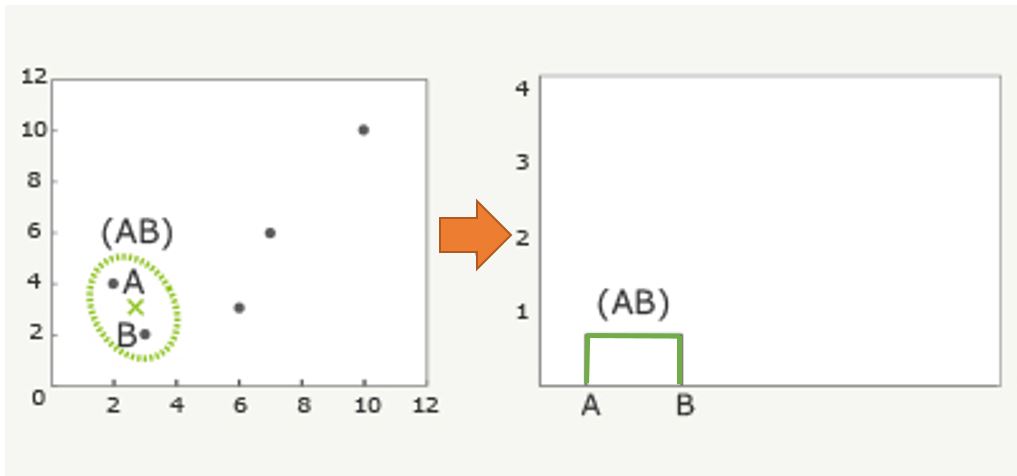
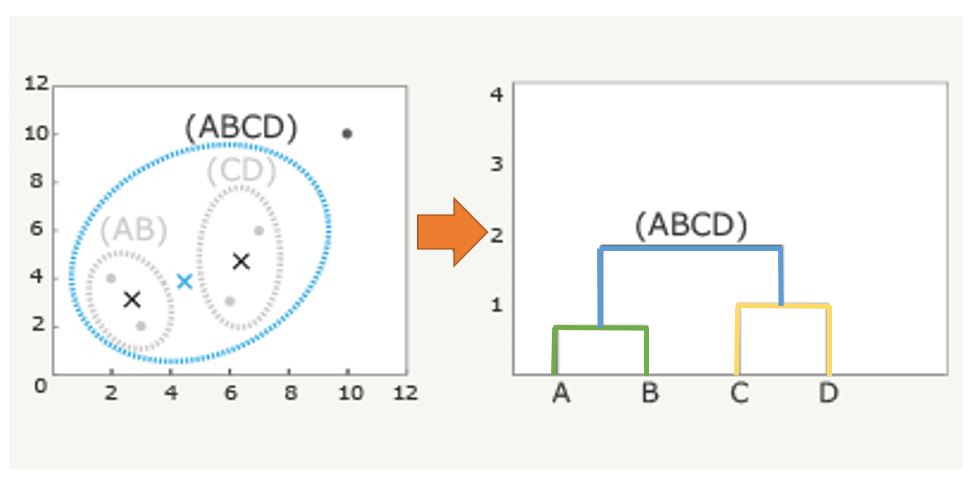
①A~Eの点で最も距離の近い組み合わせはAとB。そこで、まずはAとBをペアにする。次にこの2点の代表点(例えば重心)を求め、(AB)の×とします。
②(AB)の重心x、C、D、Eの4点で、最も距離の近い組み合わせを見つけます。ここではCとDが最も近いことが分かるので、CとDをペアーにします。この代表点を(CD)の×とします。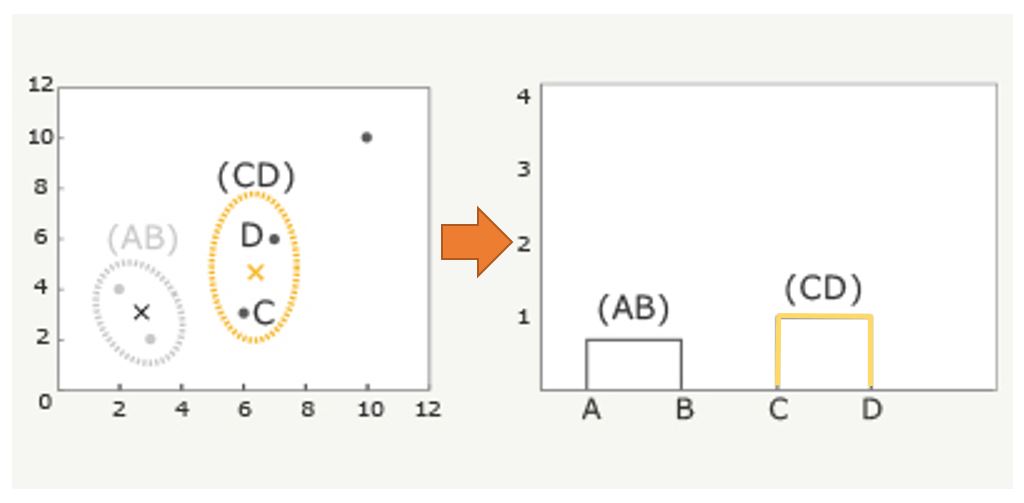
③AB)、(CD)、Eの3点で最も距離の近い組み合わせを見つけます。ここでは(AB)と(CD)が最も近いことが分かるので、(AB)と(CD)をペアにします。この代表値を(ABCD)の×とします。
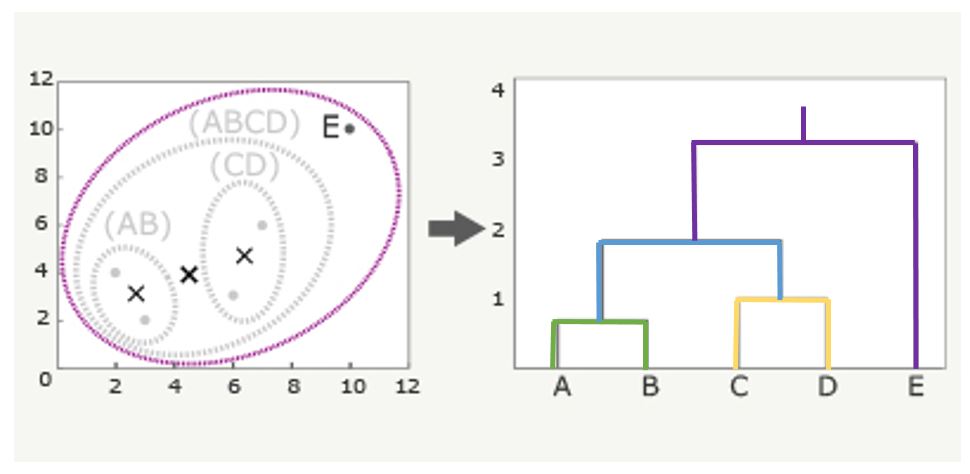
最後にEをペアにして樹形図にすると下図のようになります。この時、AとBの上にある直線が、AとBの距離を表し、CとDの上にある直線がCとDの距離を表します。
クラスター間の距離測定方法 ウォード法(Ward’s Method)
クラスター間の距離測定方法はウォード法、群平均法、最短距離法、最長距離法等があるが良く用いられるウォード法について解説します。
ウォード法は、それぞれのデータの平方和(それぞれのデータと平均値の差を二乗した値の和)を求め、平方和が小さなものからクラスタを作っていく手法です。
平方和はデータのばらつきを表すもので、平方和が大きいほどデータのばらつきが大きい(似てない)、逆に平方和が小さいほどデータのばらつきは小さい(似ている)ということになります。
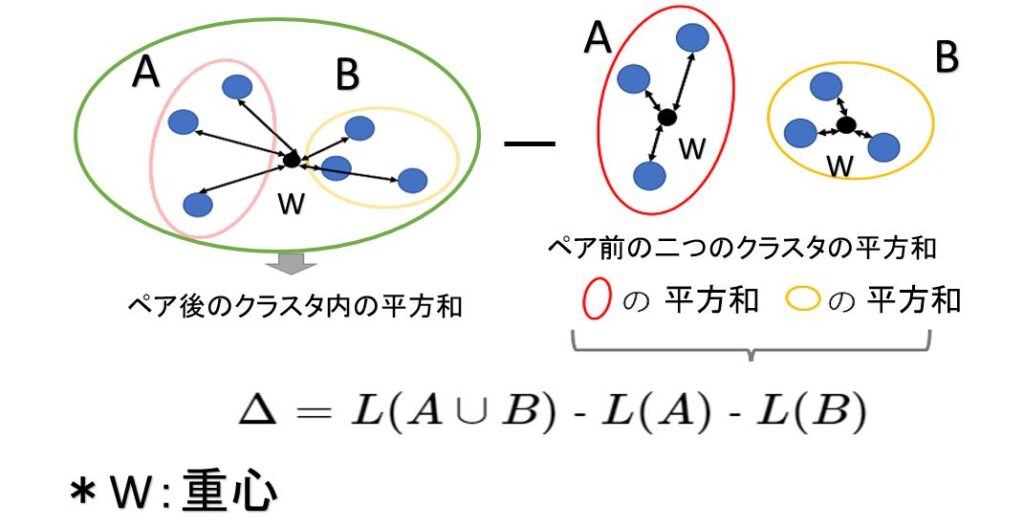
例えば2つのクラスターA,Bを結合したと仮定したとき、それにより移動したクラスターの重心とクラスター内の各サンプルとの距離の平方和L(A∪B)と、元々の2つのクラスター内での重心とそれぞれのサンプルとの距離の平方和L(A),L(B)の差
$$Δ= L(A∪B)-L(A)-L(B)$$
が最小となるようなクラスター同士を結合する手法です。
Δの値を情報ロス量という。
ウォード法による階層的クラスター分析 事例
データを準備します。
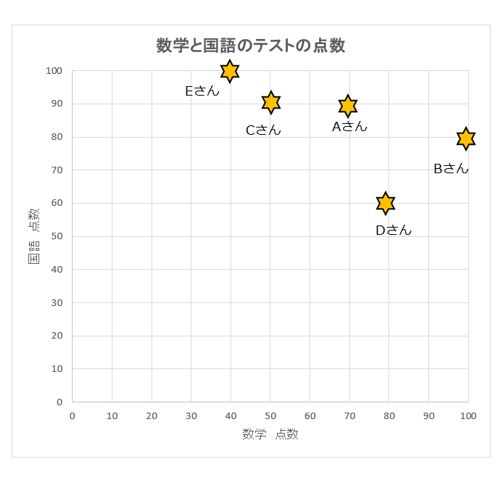
| 名前 | 数学 | 国語 |
|---|---|---|
| Aさん | 70点 | 90点 |
| Bさん | 100点 | 80点 |
| Cさん | 50点 | 90点 |
| Dさん | 80点 | 60点 |
| Eさん | 40点 | 100点 |
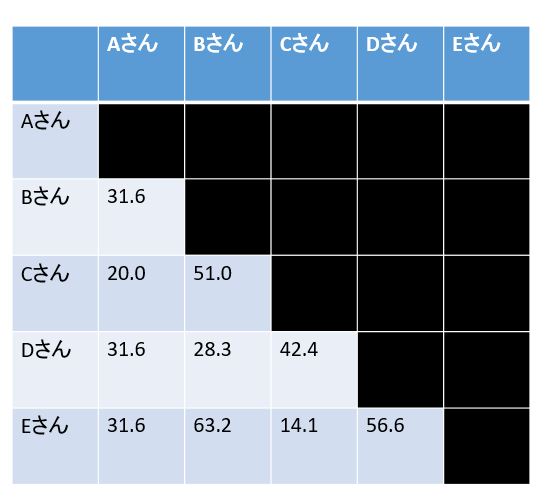
全ての要素同士の「距離」を計算
「鈴木さんと木村さんの近さ」「鈴木さんと田中さんの近さ」等を「ユーグリッド距離」を用いてを数値化します。
「ユーグリッド距離」とは定規で計測した2点間の長さの事であり、5人の点数データを図にして、ユーグリッド距離で任意の2人の距離をモノサシで測定して数値化します。
ペアを作る
全てのペアについて距離が計算できたので、いよいよグルーピングしていきます。
第一歩目は簡単で、一番距離が小さいものをくっつけます。
この例で言うとCとEが14.1で一番小さいですので、まずはCとEをくっつけます。
ここからはもうCとEは一つのカタマリで離れることはありません。
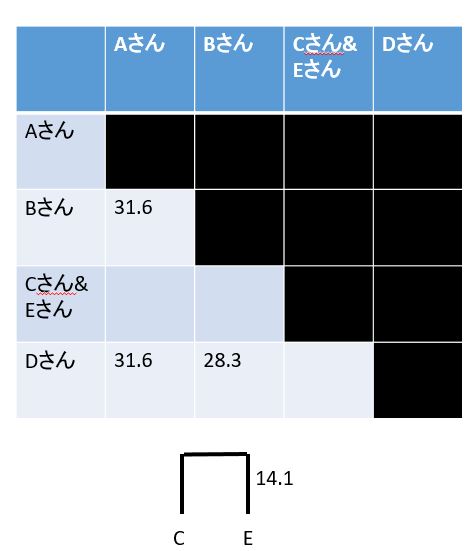
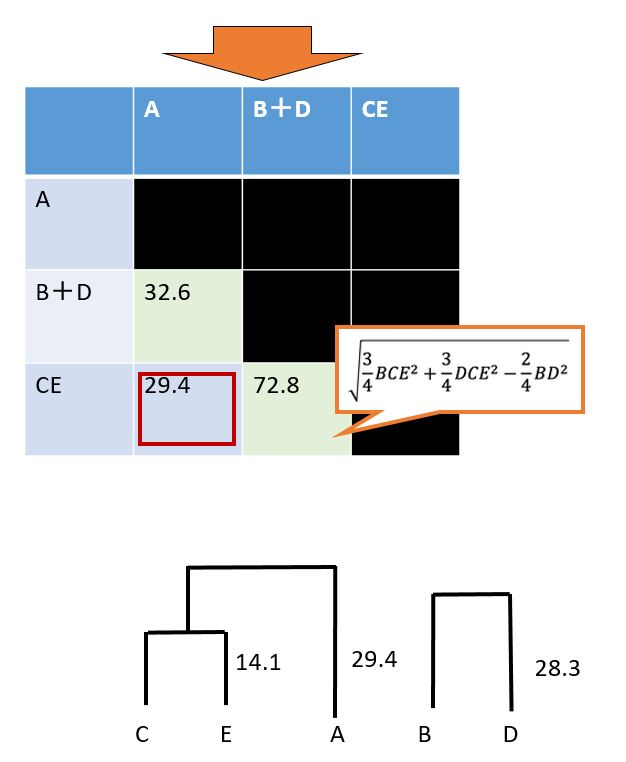
CとEが一心同体になったので、データの数が5から4に減り、「行列」も5×5から4×4ににします。
しかし、新しくできた関係「AとCE」「BとCE」「DとCE」の距離が分からないので、埋められません。
この新しく定義しないといけない距離の計算方法は「ウォード法」「最小距離法」「最大距離法」「群平均法」で異なります、ここでは「ウォード法」での「新しい距離」の計算方法を見ていきます。
ウォード法での新しい距離の計算
ウォード法は、「チームのばらつき具合(分散)」が最小になるようにデータを結合していく方法です。
先程の例で言えば、「AとCEのバラツキ」から「Aのばらつき」「CEのばらつき」を引いた値を「AとCEのバラツキ」とするわけです。
分散の計算が入るので少々計算が面倒ですが、以下の式に従うと1つ前の行列の状態から「距離の更新」を行うことができます。
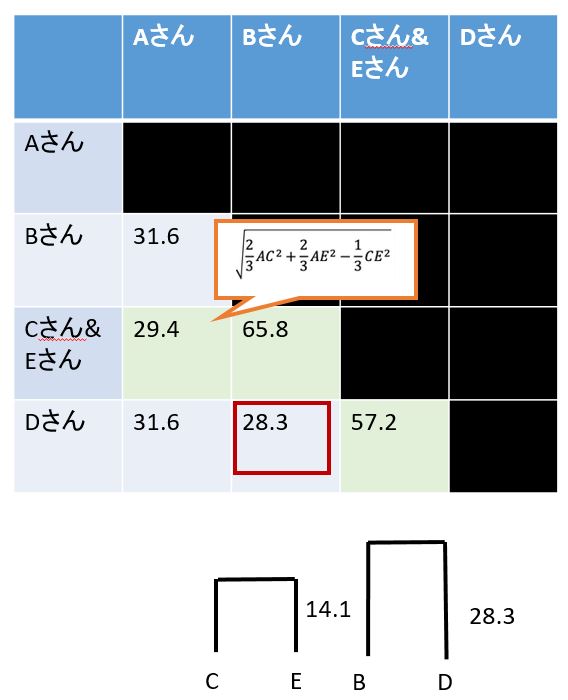
この式に当てはめると、「AとCE」の距離は29.4となり、「BとCE」は65.8「DとCE」は57.2になります。
よって、一番距離が小さいものBとDが28.3で一番小さいですので、BとDをペアにします。
次にBとDがペアになったので、データの数が4から3に減り、「行列」も4×4から3×3に変更します。
再度、ウォード法で計算して、一番距離が小さいものAとCEが29.4で一番小さいですので、AとCEをペアにします。
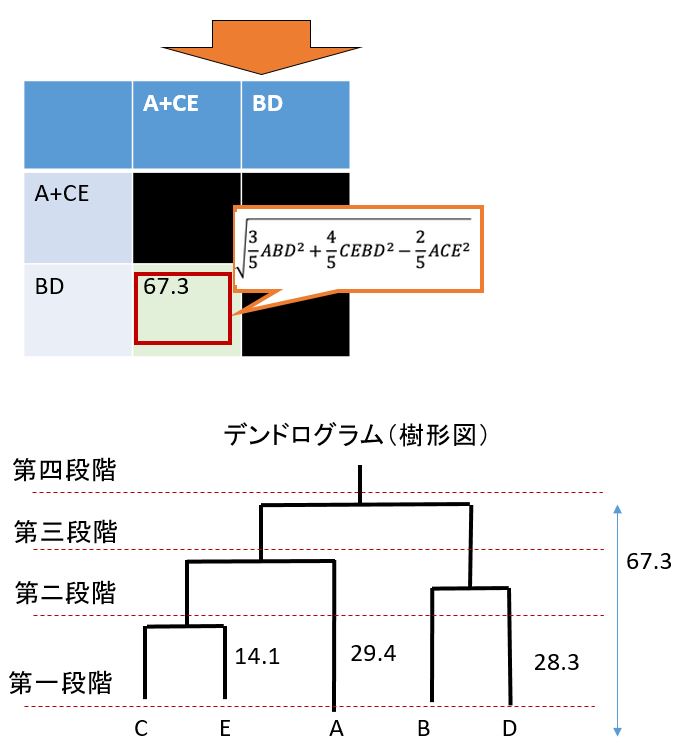
最終、AとCEがペアになったので、データの数が3から2に減り、「行列」も3×3から2×2に変更します。
再度、ウォード法で計算して全てのデーターを結合させてデンドログラム(樹形図)を完成させます。
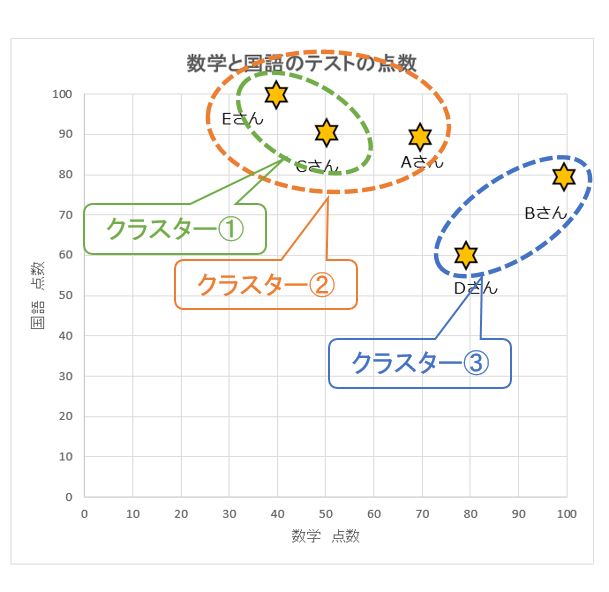
完成したデンドログラム(樹形図)を見ると分類の第一段階は全てのデータ数となりますので5つになります。
次に第二段階ではCEのクラスター①と4つのデータ。
第三段階はふたつのクラスタークラスター②と③
最後の第四段階ではひとつのクラスタになります。
上記の結果と散布図『数学と国語のテストの点数』を重ね合わせると第三段階のふたつのクラスター②③が最適なグルーピングであると推定され、これを基に予測して改善を検討します。
非階層的クラスター分析
非階層クラスタリングは階層を作らずにデータをグルーピングしていく手法のことです。
母集団の中で近いデータをまとめて、指定された数のクラスタに分類していきます、非階層クラスタリングでは事前にクラスタ数を決めて指定しておく必要があります。
あらかじめ決められたクラスタ数に要素を分けていくため、すべてのデータ同士の距離を計算する階層クラスタリングよりも計算量が少なく済みます。そのため、データ量の大きいビッグデータの分析にも適した手法です。
非階層クラスタリングの代表的な手法として、k-means法があります、k-means法はあらかじめ指定されたk個のクラスタに、平均(means)を用いて分類する」という意味で名付けられました。
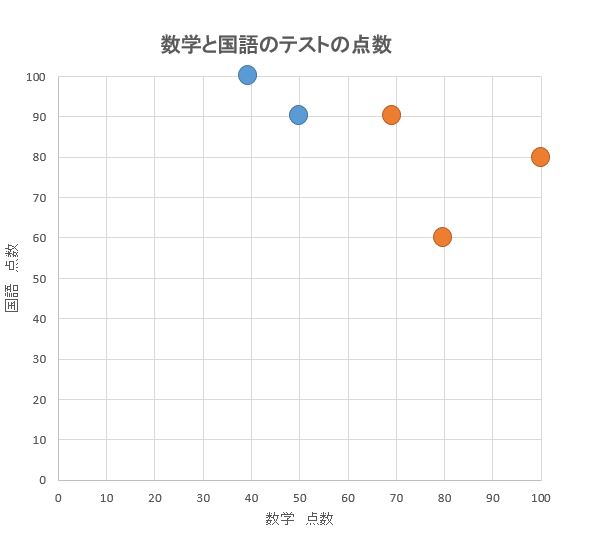
k-means法による非階層的クラスター分析 事例
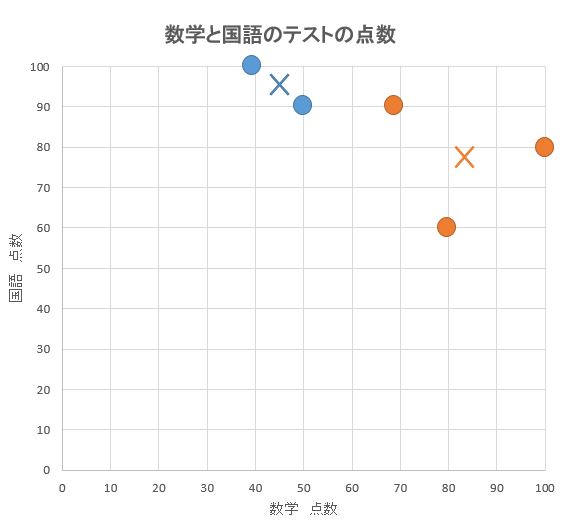
k-means法の概要を「国語」と「算数」のテスト結果を基に2次元(x軸とy軸)でご説明します。
①グループ数を決定
作成者が適当に何グループに分割するかを決定。
事例ではグループ数=2としてみます。
②グループを割り当てる
すべての点を2グループのいずれかに適当に振り分けます。
③グループごとの重心を求める
グループごとに、その重心を計算します。(図中の✕記号)
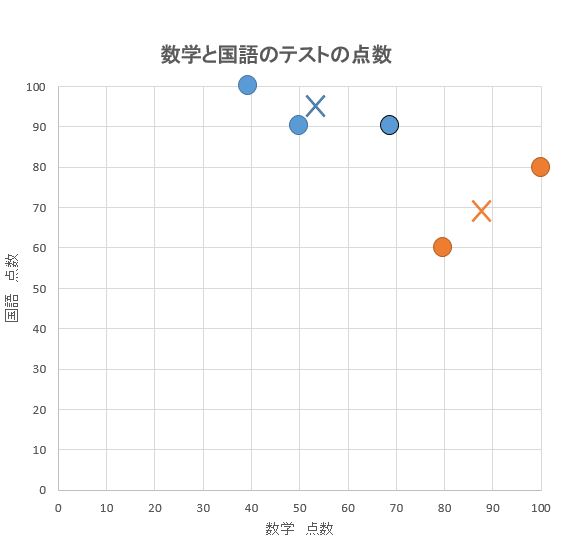
④全ての点を最も近い重心のグループに再配置
⑤.新グループで再度、重心を求める
グループが変わったので、それぞれの重心も変わります。再度、重心を計算します。
以上の作業を、グループが変わらなくなるまで何度も繰り返します。
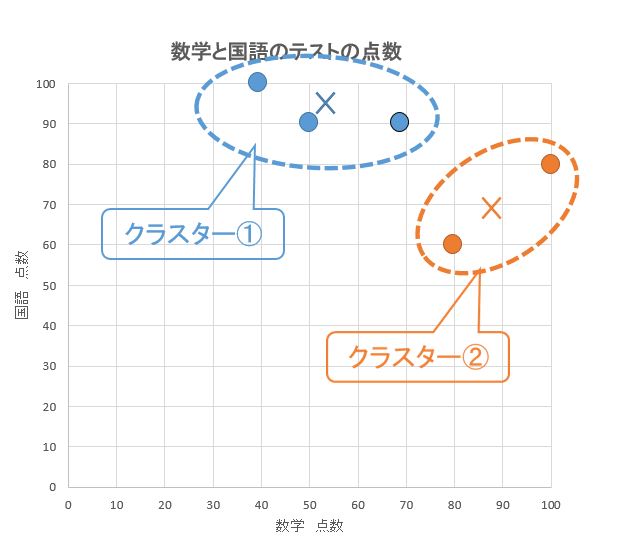
⑥ グループが変動しなくなったらグループ分け完了
グループが変わらなくなったら、処理完了です。すべての点を2グループにクラスタリング完了。
データーの予測 多変量データ解析
データを予測する場合にも色々な多変量データ解析が用いられます。
データを予測する場合
データを予測する場合には、次の手法を使います。
| データ予測手法名 | 使用場面例 |
| 回帰分析 | 顧客アンケートなどで、ある項目の評価を別項目の評価から予測する |
| 重回帰分析 | 顧客アンケートなどで、総合評価を個別の項目評価から予測する |
| ロジスティクス回帰分析 | 1日の喫煙本数と1ヵ月間の飲酒日数から、がん発症との関連性を分析する |
| 判別分析 | いくつかのグループが、どのような基準で分けられているのか分析する |
| パス解析 | 要素をパスで結んだパス図を用い、要素間の因果関係や相関関係を分析する |
| 分散分析 | 商品AとBで高い評価をされているのはどちらか分析する。ABテストとも呼ばれる |
| コンジョイント分析 | 製品のどの属性によって評価がなされているのかを分析する |
データサイエンスでは、分類以上に重要な分析はデータに基づいて予測を行うことです。
この目的のため、最もよく利用されるのが回帰分析です。
回帰分析では、要因と結果の関係をモデル化してデータ解析を行いますが使用するデータは、連続変数や離散変数の量的データを前提とします。
回帰分析で予測
2つの変数について、下の左図は一方の数値が大きければ他方の数値も大きくなる傾向を示しています、これらの傾向は、分布の形状が直線に近くなるほど相関関係が強くなることを意味し、相関係数の絶対値は1に近づいていきます。
このような相関関係が変数間に確認できると一方の変数の数値から他方の変数の数値を予測することが可能になります。それを行うデータ解析の方法が回帰分析です。
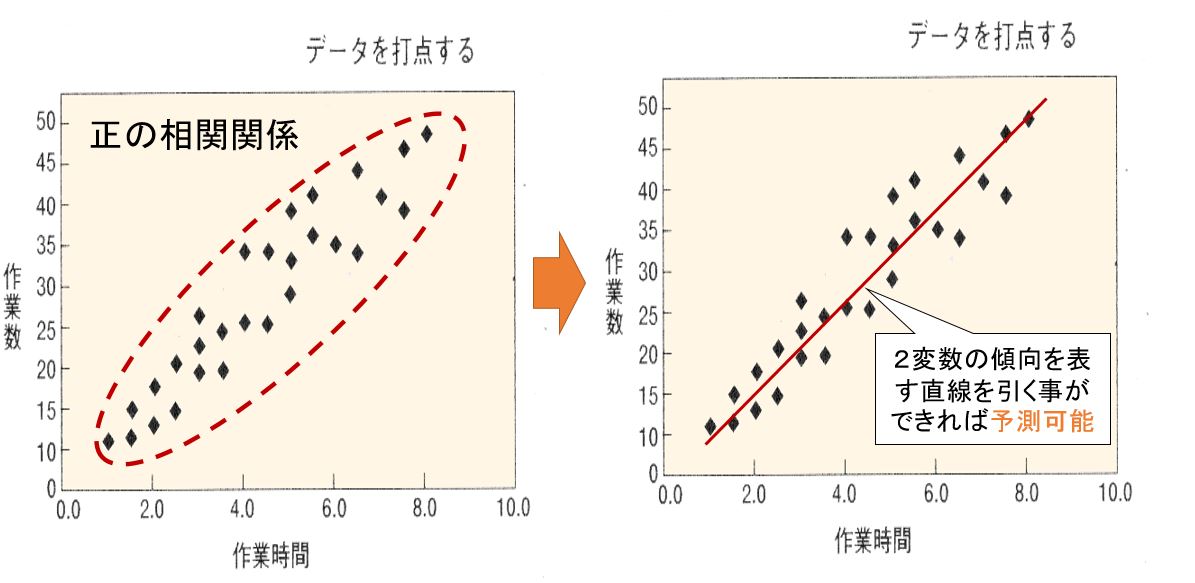
たとえば、下の左図のような正の相関の場合はデータポイントの分布が右上がりの傾向を示していますので一方の変数の変化量に対して、他方の変数の変化量がほぼ一定の割合で対応していることがわかります。
もちろん、そのような量的関係はあくまで「おおよそ」の対応関係であって1次関数のような厳密な対応関係を示すものではありません。
しかし、そのような対応関係を、1次関数の式で表現できれば、「おおよそ」の予測も可能になります。それを示しているのが下の右図です。
左図では、正の相関を示すデータポイントの集まりを赤い枠線で囲んでいます。この囲みは明らかに右上がりの楕円形をしています。
つまり、2つの変数間に一定の量的な対応関係があることを示唆しているわけです、そこで、この楕円形を代表する直線、つまり2変数の傾向を代表する直線を右図のように引くことができれば予測が可能になります。
回帰モデル
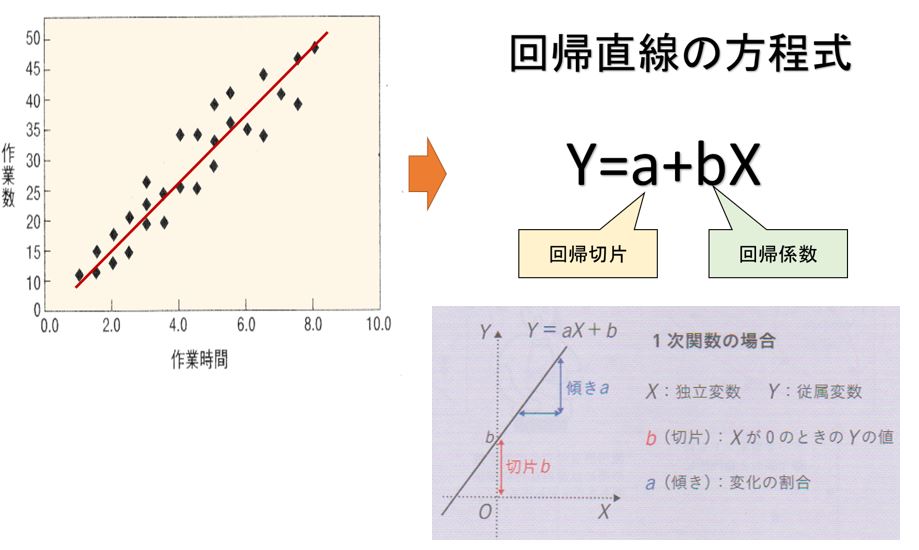
いま、横軸の変数をX、縦軸の変数をyとすると、この直線の式は、1次関数と同じように表すことができます。このような直線の式を回帰直線、もしくは回帰モデルと呼びます。
ただし、下図で示しておいたように得られた直線の方程式は、数学でいう1次関数ではないので、それと区別するためy切片に当たる定数を変数Xより前に置いて定数a(回帰切片)とし、変数Xに係る変化の割合を定数b(回帰係数)として定式化します。
繰り返しになりますが回帰分析では2つの変数の間に相関関係があることを前提とします。従っ下図の回帰モデルでは変数Xとyに一定の相関関係がなければなりません。
しかし、2つの変数に相関関係があれば直ちに回帰分析が可能になるというわけではありません。それには、Xとyの間に、要因と結果という関係を想定できることが必要です。
下図でも示したように回帰モデルでは変数Xを説明変数もしくは予測因子と呼び、変数yを被説明変数と呼びます。
つまり、変数yは、変数Xによって「説明される」という意味で「被説明変数」、変数Xは、変数yを「予測する要因」という意味で「予測因子」と呼ばれるます。
このことからもわかるように、たとえば、下図の回帰モデルの場合は、変数Xが要因であり、その結果が変数yであるという関係を想定しているので相関があるとはいっても X=a十bYという回帰直線を想定することはできません。
回帰分析 事例
例えば、血圧y(収縮期血圧)と年齢Xという関係を調べます、一般に年齢が高くなるほど血圧が高くなると言われています。
そこで、血圧に影響を与えるその他の要因(喫煙や食生活など)はすべて同一である対象者を何人か選んで年齢と血圧のデータを集めたところ確かに正の相関があれば、血圧を年齢で説明する回帰モデル
$$y=a+ bX$$
を求めることには意味があります。
つまり、血圧が高いか低いかは、年齢の影響を受けるという関係を前提とした回帰モデルです。 しかし、これを逆転させた回帰モデル
$$χ=a+ bY$$
がまったく無意味だということは明らかです。年齢が高いか低いかは血圧の影響を受けることなどあり得えません、高齢の方で血圧が低い方及び若い方でも血圧の高い方もいます。
回帰係数と回帰切片を推定
このように、回帰分析を使用に当たってはまず相関のある変数が要因と結果として適切に定式化できるかどうかを検討する必要があります。その上で、回帰分析を行うわけですが具体的には回帰係数と回帰切片という2つの定数をデータから推定することになります。
それによって回帰モデルが確定できれば任意の変数Xの数値に対応した変数yの予測値を求めることができます。
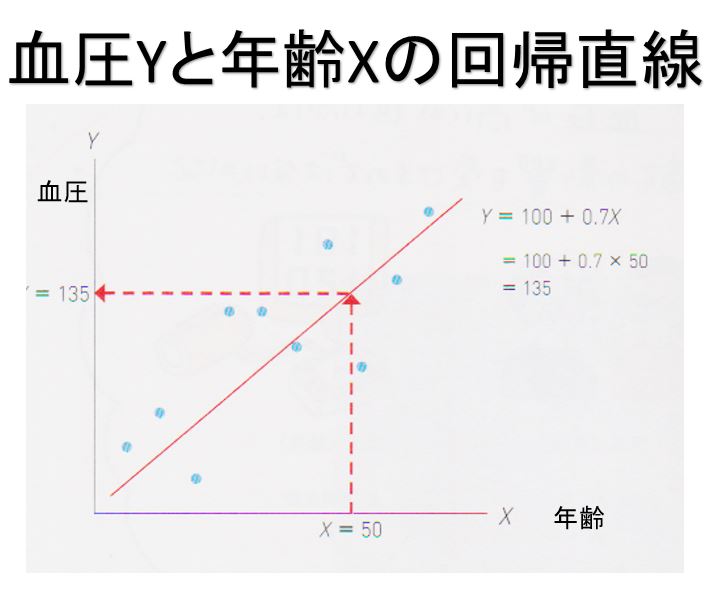
血圧と年齢の事例で言うと集めたデータから推定した結果、回帰係数が0.7と回帰切片が100であったとするならば、たとえば年齢50歳の人のおおよそ血圧は135であると予測できます。
回帰分析で予測する一肥満度から血圧の値を予測
保健師の鈴木さんは担当する地域住民50人に対して健康調査を行い、集めたデータから、肥満度と血圧(収縮期血圧)の回帰分析を行うこととしました。
一般に、肥満は高血圧の原因の1つであるとされているので鈴木さんはまず肥満度と血圧に正の相関関係があるかどうかを確認するため、身長と体重のデータを用いて肥満度の指標であるBMI値を計算し、その数値と血圧の相関関係を調べてみました。
計算の結果、相関係数は0.62となり、やや強い正の相関関係が示され、散布図からも右上がりの関係を確認できました。
最小2乗法で回帰係数や回帰切片を推測
次に鈴木さんは目的である肥満と血圧の関係を定式化するためBMI値を説明変数X,血圧を被説明変数yとして回帰分析を行いました。
なお、通常の回帰分析の場合、回帰係数や回帰切片の推定方法には最小2乗法と呼ばれる方法が用いられます。
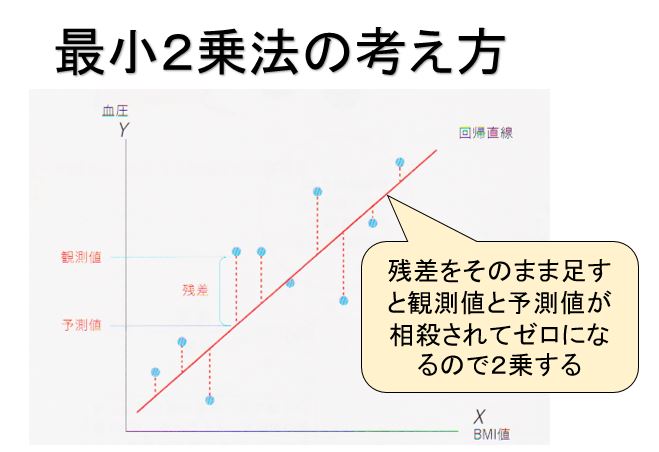
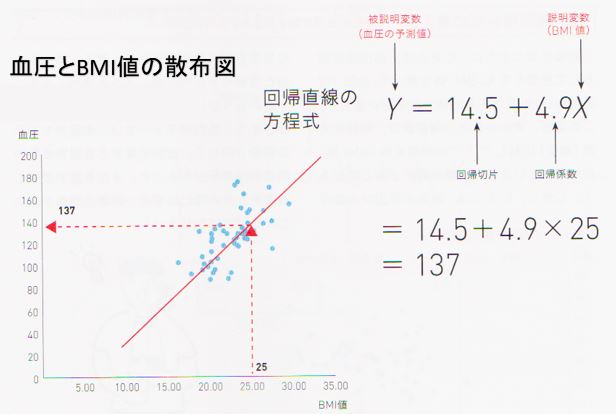
下図で示されているように、最小2乗法というのは変数Xのデータポイントを回帰モデルの式に代入して得られる予測値と変数yの実際のデータポイントとの乖離(残差:点線の部分)が最小になるように回帰係数と回帰定数を決定する方法です。
より正確に述べると乖離の2乗の合計が最小になるように推定値を求める方法でこのため「最小2乗法」と呼ばれます。
鈴木さんも最小2乗法を用いて、回帰係数と回帰切片を求めています。その結果、得られた推定値はで回帰係数が4.9、回帰切片が14.5となりました。図でも示されているようにこの結果に基づくと肥満の基準値であるBMI = 25では、血圧の予測値が137 (=14.5+か9×25)となり、肥満は高血圧(130以上)のリスクの1つになることがわかります。
Cさんの回帰分析は、被説明変数に対して1つの説明変数だけで予測を行うものでした
が、説明変数の数はいくつでも増やすことが可能です。
このように、回帰分析はシンプルで汎用性があることから、最も代表的な予測のための
手法であり、さまざまな分野で応用されています。
データリテラシーの鍛え方、活用
データの信頼性
現在は高度情報社会であり非常に多くの情報、データが溢れています、しかし多くの捏造された情報、根拠のないデータが巷に溢れています。
如何に精度の高いコンピュータでAI分析にしてもInputである基のデータの信頼性が低いなら結果、正しくないOutputしかでません。
また、過去30年のあいだに、マスコミの報道量は格段に増えました、テレビのチャンネル数の増加は凄いもので全チャンネル数×24時間の隙間を埋めるため、製作費が安くつくワイドショーなどの情報バラエティ番組が増えています、情報バラエティ番組は、報道番組ではなく娯楽番組であり、データーの信頼性は低いです。
これにさらにネットニュースが加わっています、これは新聞やテレビを主なニュース源としていますが信頼性は低い情報です。
人は幸福な情報より不幸な情報を好みますので視聴率を上げるためにマスコミはそのような情報をばかりを垂れ流しします。
高齢者の運転による死亡事故
高齢者の運転による事故が問題になっています、ワイドショーなどの情報バラエティ番組で良く取り上げています。
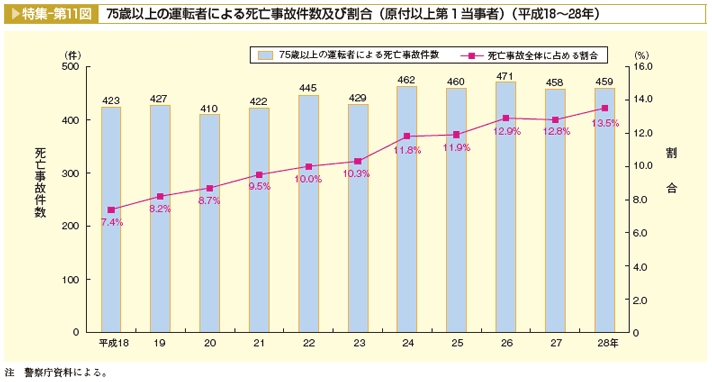
下図は75歳以上の運転による死亡事故の件数と割合が平成18 (2006)年から平成28年にかけてどう変化したかを示すものです。件数はあまり増えていませんが、全体の死亡事故に占める割合は2006年の7.4%から2016年13.5%に増加しています、約1.8倍です。
75歳以上の人口は2006年には1,164万人、全人口の9.1%でした。 2016年には1,632万人、12.8%に増えていますこちらは約1.4倍です。
したがって全死亡事故に占める75歳以上の運転者の事故の増加の約半分以上は75歳以上の高齢者が増加したためです、よって高齢者が増えていくのですから当然、高齢者の運転による事故は増えると推測されます。
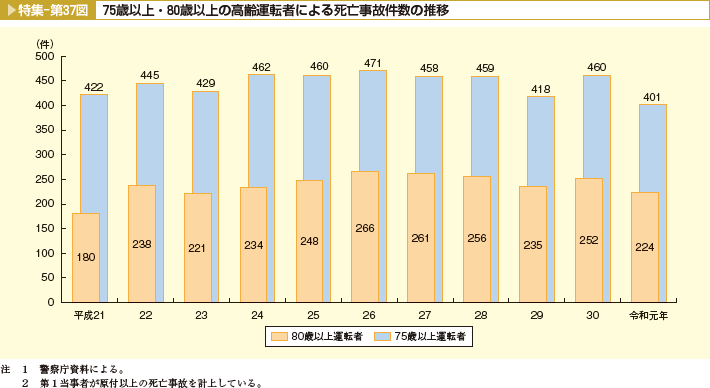
しかし、下の図からは75歳以上の運転による死亡事故の件数と割合が平成21年から令和元年にかけてどう変化したかを示すものですが高齢者の人口が増えているのにも関わらず、件数はあまり増えていません。
よって物事を判断する為には一つのデータ、情報だけで判断するのは危険であり、様様なデーター、情報を収集して分析する必要があります、この時にデータリテラシーが活かされます。
上記の例では確かに高齢になると反射神経は落ちますが逆に若者と比較すると運転経験が豊富なのでスピードは出さず、安全運転を心がけるようになり、事故がおこさなく人もおり、一概に全ての高齢者が事故を起こすリスクが高くなるとは言えません。
正しく論理的に分析する為には一つの思い込み(分類)で行うのではなく、データー自体で分類できるように科学的に分析する必要があります。
分析する前から恣意的に分類およびサンプリング方法が決まっていては如何に時間をかけて収集したデータも無意味になります。
偽薬効果、プラセボ効果の検証 クロス集計
新型コロナに感染して重症化した30人にある薬を飲んで貰い、内18人が症状に改善がみられたとします、その薬は有効だと考えていいのでしょうか?
人の体は自然に病気を治す免疫力を持っています。ですから、その薬を飲まなくても症状が改善します。
新型コロナ感染し重症化した20人には薬を与えないで自然に回復するかどうかを見ました。 20人中11人に症状の改善がみられました。
下表に2つの結果をまとめます。
このような表を2×2表と呼びます。より一般的なクロス集計という言葉が使われることもあります、必要に応じて2×2表で考えることはデータにごまかされない為の簡単な一つの方法です。
新型コロナウイルス飲み薬服用の症状改善 クロス集計表 事例
| 症状良化 | 症状良化せず | ||
| 薬服用 | 18名 | 12名 | |
| 薬飲まず | 11名 | 9名 | ←対照群 |
薬を飲んだとき、症状が改善した人の割合は18/30=0.60、薬を飲まなくても症状が改善した人の割合は11/20 = 0.55ですから、薬の効果があったかどうかは統計的検定で検証する必要があります。
偽薬効果
上表の行、「30人にある薬を飲んでもらって、うち18人が症状に改善がみられた」にたいして、下の行を対照群(control group)と呼びます。
新たに開発された薬の効果を調べるために、偽の薬を飲むグループを対照群としたところ、ほとんど違いがなかったという事例は多く、これを偽薬効果(placebo effect)と言います。
偽薬にあたる英語(placebo)を用いてプラセボ効果、あるいはプラシーボ効果というのが普通です。
医者が「これは偽薬ですから効果はありませんよ」と説明して渡しても、本物の薬と効果にたいした違いはなかったという事例もあります。
新型コロナウイルスを治療に当たる専門医者は内科医の方です、しかし、その方に薬服用の効果を聞いても正しい答えは得ることはできません、何故なら全てのお医者さんは統計家ではないからです、よって、正しい答えを知る為には統計の専門家、データサイエンティストに効果を聞かなければなりません。
ランダム化比較試験と二重盲検法
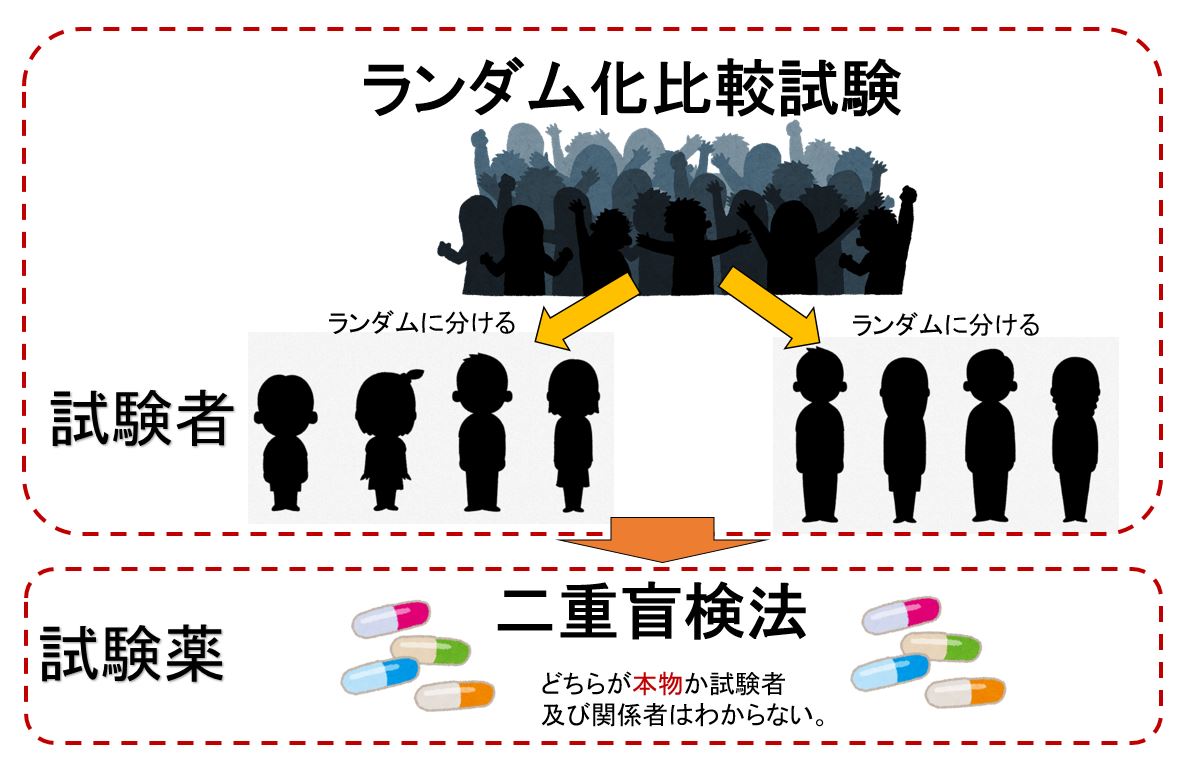
このような偽薬や他の薬との比較試験をするさいには、患者をランダムに2つのグループに分けます。これをランダム化比較試験(randomized controlled trial)と言います。
このとき、さらにランダム化比較試験doble blind metod)というやりかたがとられます、二重盲検法は、どちらの薬か(本物の薬か偽薬か)が、患者にも医者にもわからないようにランダムに割り当てる方法です。
事例として1980年代前半に認知症に効果があるとして販売が許可にされて薬がありました、しかし、1990年代前半に二重盲検法によるランダム化比較試験を行ったところ、効果がない事がわかり販売が取り消されたという例もあります。
癌検診と精密検査一誤検出と見逃し
がんであるかないかを簡単に検査する画期的な方法が開発されたとしましょう。その検査で10,000人をテストしました。そのうち、がんであると判定された人は200人、そのなかで実際にがんであった人は40人だったとします。
つまり、160人/200人=80%の人を誤ってがんだと検出したことになります、これを誤検出率80%と言います。誤検出をしても病気の点では大問題ではありませんが精密検査で無駄な費用や時間がかかるというマイナス面があります。
癌判定患者200名の精密検査結果:
| 癌 有無 | 陽性 | 陰性 | 合計 |
| 人数 | 160名 | 40名 | 200名 |
次にもっと大切なのは、実際にがんである人をどれだけ正しく検出できるかです、実際にがんであった人45人のうち、検査でがんであると判定された人は40人であったとします。
5人が見逃し(検出洩れ)です、 5/45= 11%を見逃し率、あるいは検出洩れ率と言います。
この結果を表にまとめます。
癌判定検査の検出洩れ率:対象:10,000人のうち45名が癌患者
| 判定結果 | 判定OK | 判定ミス | 合計 |
| 人数 | 40名 | 5名 | 45名 |
実際のがん検診のデータで検証してみます。
乳がんは、精密検査を勧められる大が多いことで有名です、日本対ガン協会のデータによると、乳がん検診を受けた人126万1551人の内、精密検査が必要と判定された人の割合は 4.47%です。
その91%が実際に精密検査を受診しそのうちがんが発見された人の割合は5.9%、3043人でした。検診を受けた人の0.24%です。
乳がん検診を受けた人のうち、約22人に1人は「精密検査が必要」と言われますがそのうちの17人に1人しか、乳がんの人はいないのです。
精密検査が必要と判定されても、実際に乳がんである人は17人に1人しかいないのは、乳がんである人(3043人)よりも、乳がんでない人(1261551- 3043 = 1258508)のほうが圧倒的に多いからです。
しかし、がんであることを見逃すと大変ですから、乳がん検診における見逃し率(検出洩れ率)を0に近く抑えるために、少しでも怪しい人は精密検査に回すようにしているのです。
 「線虫がん検査」の信頼性
「線虫がん検査」の信頼性
現在、「線虫がん検査」というトピックが話題になっています、 線虫とは「線形動物」というカテゴリーに属する長さ0.3-1mm程度の小さく細長い生き物です。この線虫には「嗅覚が非常に発達している」という特徴が存在します。
ある条件下において、線虫がヒトの尿に含まれる「がん」の匂いを感知する特性を、がん検診に利用するという試みが注目を集めています。
この検査は「リキッドバイオプシー」と呼ばれ、近年非常に研究が活発に進められている検査手法の一つです。
基本的に医療機関で行われているがん検診は胃X線検査(バリウム検査)、胃カメラ、大腸カメラなど体に一定の負荷をかけて体内のがんの存在の有無を確かめる方法が基本です。
一方、リキッドバイオプシーでは血液や尿などを採取し、液体(=リキッド)の成分からがんの存在を捉えにいくという、受け手にとっては非常に簡便で、体に負担のかからない検査方法になります。
しかし、信頼性が低いです。
結論から申し上げると、「現段階では」統計的にオススメできる手法ではありません。
現状、線虫がん検査は有効性を検証する段階であり、強く推奨できるものではありません。
最大の問題は「偽陽性」です、偽陽性とは、実際には陰性(がんが存在しない)のに検査結果として陽性が出てしまうことです。
偽陽性の場合は、そもそもがんが存在しないのに結果として陽性の宣告を受け、余計な精密検査を受ける事になる可能性もあるわけです。
統計的に見て全体の死亡率が下がっていれば有効な検査と言えるでしょうが、現状では「あまり効果のない検査を受け、偽陽性となり余計な精密検査を受け合併症が引き起こされる」という負のリスクさえ存在するのです。






































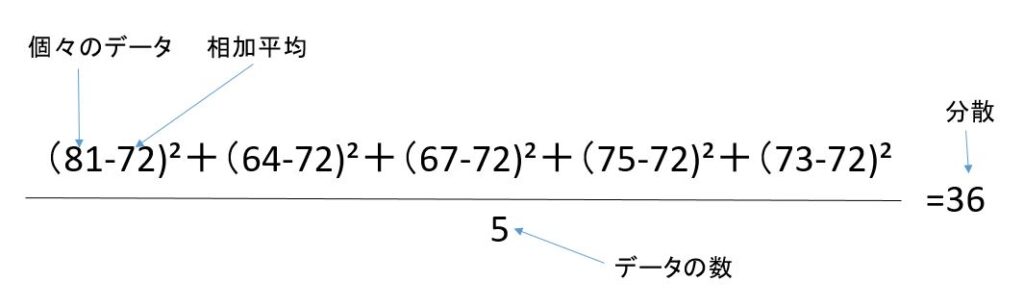


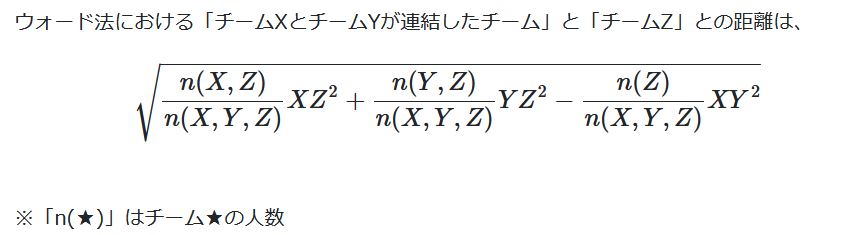





コメント