ChatGPTで「層別化・層別解析」初心者向けガイド
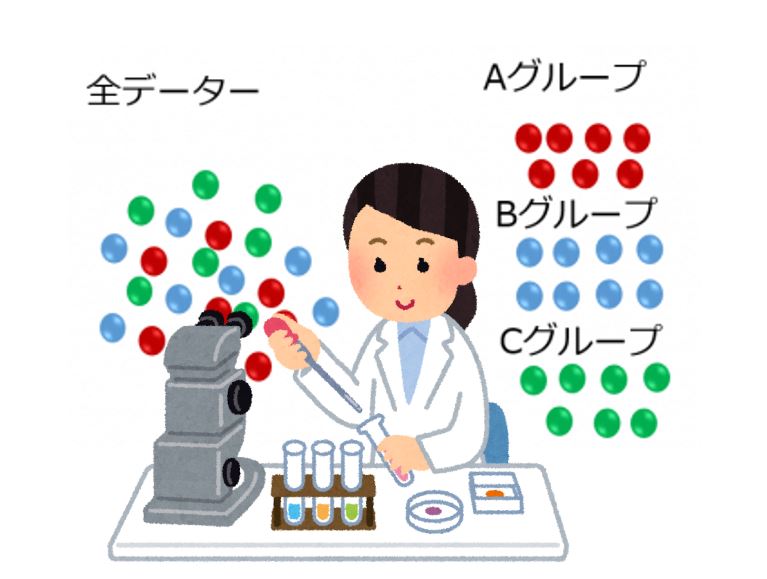
「層別」とは何か?
✔ 基本概念
「層別」とは、データを意味のあるグループ(層)に分けることです。たとえば次のような例があります:
- 製造日別(朝・昼・夜)
- 作業者別(A班・B班)
- 使用原材料別(仕入先ごと)
- 製品機種別、ロット別、ライン別…
データを層別することで「どの層で問題が起きているのか?」を可視化できます。
✔ なぜ層別が必要なのか?
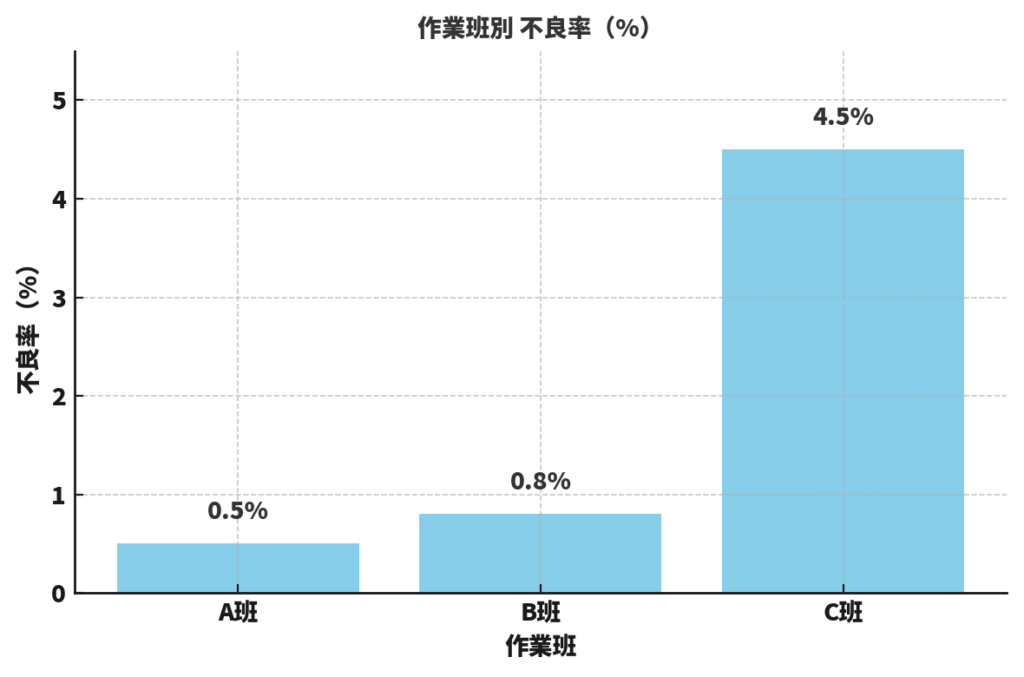
たとえば平均値で「不良率2.0%」と出ても、層別してみると:
- A班:0.5%
- B班:0.8%
- C班:4.5%
このように“真の問題”が隠れていたことが分かるのです。
*AI ChatGPTに『層別化』を依頼する前に『層別化の基本』を学ぶことにより的確なプロンプト文を指示することができます。
『基本の層別化の詳細』については下記の記事を参照 願いします。
層別分析と分散分析の違いとは
層別分析(そうべつぶんせき)と分散分析(ぶんさんぶんせき)は、どちらも「データの違い(ばらつき)」を理解するための分析手法ですが、目的・使い方・得られる結論がまったく異なります。
以下に、わかりやすく比較して説明します👇
目的の違い
| 項目 | 層別分析 | 分散分析 |
|---|---|---|
| 目的 | ばらつきの原因を「グループ(層)」ごとに分けて原因を探る | グループ間の平均値の差が統計的に有意かを検定する |
| 例 | 不良率が「作業者A・B・C」で違うかを確認したい | 作業者間で平均不良率に有意差があるかを検証したい |
🔹層別分析は、「違いを見える化する」ことが目的。
🔹分散分析は、「その違いが偶然ではないといえるか(統計的に有意か)」を判断する。
分析方法の違い
🔹層別分析では「層ごとの特徴」を肉眼で確認するのに対し、
🔹分散分析では「差がある」と数値で裏付ける。
使う場面の違い
| フェーズ | 層別分析 | 分散分析 |
|---|---|---|
| 現状把握 | ✅有効(どの層に問題があるかを確認) | ❌まだ早い(原因特定前) |
| 仮説検証 | ⚪一部利用 | ✅有効(差が統計的に有意か確認) |
例:
-
まず層別分析で「Aラインだけ不良が多い」と見える化。
-
その後、分散分析で「Aラインと他のラインの差が有意か?」を確認。
👉 両者はセットで使うと最強!
具体例
データ例:
-
グループA:12, 15, 14, 13
-
グループB:10, 11, 9, 12
-
グループC:8, 9, 7, 8
層別分析:
箱ひげ図でAが全体的に高く、Cが低いとわかる。
→ 「グループによって違いがありそう」と視覚的に判断。
分散分析:
F値 = 18.5、p値 = 0.001 なら
→ 「差は偶然ではない。グループ間で平均に有意差あり」と結論づけられる。
比較表
| 観点 | 層別分析 | 分散分析 |
|---|---|---|
| 例え | ルーペでデータを観察 | 顕微鏡で統計的に証明 |
| 性格 | 定性的・探索的 | 定量的・検証的 |
| 最終目的 | 問題点を見つける | 仮説を検証する |
実務的な流れ(QC的視点)
1️⃣ 層別分析で「違いがあるか」を確認
→ 人・機械・材料・方法・時間などで層別。
2️⃣ 分散分析で「その違いが有意か」を確認
→ 改善の優先順位や対策の裏付けを得る。
分散分析については下記の記事を参照 願いします。
関連記事:ChatGPTで簡単に分散分析を解説:実事例とともに学ぶ!

ChatGPTで層別化をサポート
✔ できること
AI ChatGPTを使えば、以下のようなサポートが可能です:
| 作業 | ChatGPTでの支援例 |
|---|---|
| 層の設定 | 「勤務シフト別に分類して」と指示 |
| 層別グラフ作成 | Pythonコードでグラフ自動生成 |
| 層別ごとの傾向分析 | 「各班の不良傾向を比較して」と依頼 |
| 対策提案 | 「不良率が高いC班の対策は?」と聞く |
ChatGPTへの基本プロンプト例
初心者でもすぐ使えるプロンプト例を紹介します。
プロンプト例①:層別分類を指示
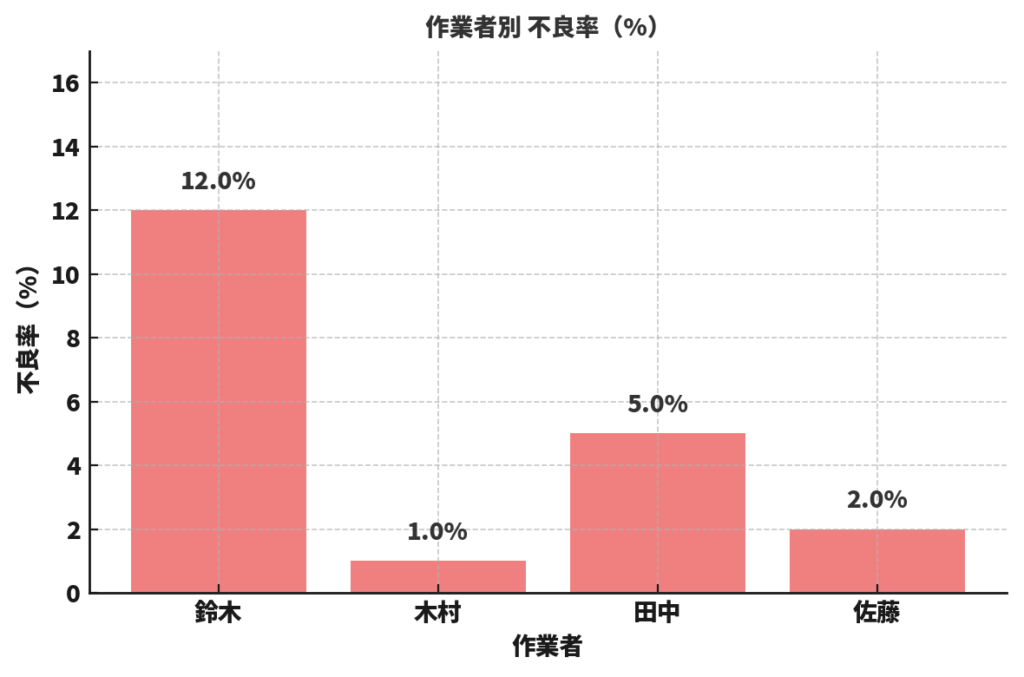
下記の不良データを「作業者別」に層別してください。
各作業者ごとに不良率を集計し、棒グラフで可視化してください。
鈴木 不良数 12 生産数 100
木村 不良数 1 生産数 100
田中 不良数 5 生産数 100
佐藤 不良数 2 生産数 100
🔶 プロンプト例②:層別結果から原因を探る
層別したデータの中で不良率が最も高い層の特徴と、考えられる原因を分析してください。
以下に、層別データから不良率が最も高い層(作業者:鈴木)の特徴と考えられる原因を分析します。
不良率が最も高い層:鈴木(12.0%)
特徴
- 生産数は他の作業者と同様(100個)
- 不良数が12個と突出して多い
- 他の作業者と比べて 2〜12倍の不良率
考えられる原因(仮説)
| 分類 | 原因の仮説 | 補足 |
|---|---|---|
| 作業スキル | 作業手順の理解不足、訓練不足 | 経験年数が浅い可能性、教育機会の不足 |
| 注意力・集中力 | 他の作業と並行して作業している | 複数ライン担当や疲労による注意力低下 |
| 使用設備 | 鈴木だけ特定の機械を使用している | 使用設備が他と違い、不良が発生しやすい |
| 材料ロット | 特定ロットの材料を使っていた | 原料ロットによる品質差も考慮すべき |
| 作業時間帯 | 夜間・深夜に作業していた | 時間帯でのミス増加傾向(生体リズム) |
| 測定方法 | 測定ルールが他者と異なる | 測定基準のブレ、マニュアルの認識違い |
プロンプト例③:改善案を出す
作業者 鈴木さんの不良率が他の人より著しく高いです。考えられる要因と改善策を5つ提案してください。
作業者・鈴木さんの不良率(12.0%)が他の作業者より著しく高いことに対して、考えられる要因と具体的な改善策を5つの観点から提案いたします。
① 作業手順の理解不足
要因:
鈴木さんが標準作業手順を十分に理解していない、あるいは自己流のやり方になっている可能性。
改善策:
-
作業手順書の再確認とOJT(現場教育)の再実施
-
チェックリスト形式で作業ポイントを見える化
-
作業時に指差し呼称の導入
② 機械や道具の扱いに問題がある
要因:
使用している設備のセッティングにズレや劣化があるか、扱いが雑で機械条件が不安定になっている。
改善策:
-
使用設備のメンテナンス履歴を確認し、点検強化
-
作業者別の設備使用状況を記録して差異を可視化
-
鈴木さん専用の機械に関して専門教育を行う
③ 注意力の低下・疲労
要因:
休憩不足や作業時間帯(夜勤等)による集中力低下、あるいは過重作業による疲労が影響している。
改善策:
-
作業時間の記録と疲労度ヒアリングの実施
-
作業負荷を他作業者とバランスよく分散
-
作業時間帯の交替や短縮を検討
④ 材料・ロットの差
要因:
鈴木さんが担当するタイミングで使用している原材料や部品のロットに品質ばらつきがある。
改善策:
-
材料ロット別に不良率を分析し、相関を確認
-
原材料の受け入れ検査と保管管理の見直し
-
作業記録にロット番号を紐づけるトレーサビリティ強化
⑤ 作業環境(照明・気温・配置)
要因:
鈴木さんの作業場所だけ照度が暗い、空調が当たらないなど、環境条件が不利な可能性。
改善策:
-
作業場所の5S点検と環境調査を実施
-
レイアウト変更や照明改善などの環境是正
-
作業者からのフィードバックを積極的に取り入れる
Pythonで層別グラフを描く(Google Colab対応)
ChatGPT プロンプト文
下記のデーターの層別グラフを作成するPythonコードを教えてください。
鈴木 不良数 12 生産数 100
木村 不良数 1 生産数 100
田中 不良数 5 生産数 100
佐藤 不良数 2 生産数 100
♯条件:各作業者ごとに不良率を集計し、棒グラフで可視化してください。
♯条件:日本語フォント Noto Sans Japaneseをアップロードするコードも含む
回答Pythonコード
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
# データ定義
data = {
"作業者": ["鈴木", "木村", "田中", "佐藤"],
"不良数": [12, 1, 5, 2],
"生産数": [100, 100, 100, 100]
}
# DataFrame作成
df = pd.DataFrame(data)
# 不良率の計算(不良数 ÷ 生産数)
df["不良率"] = df["不良数"] / df["生産数"]
# フォント指定
font_path = "/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc"
jp_font = fm.FontProperties(fname=font_path)
# グラフ描画
plt.figure(figsize=(6, 4))
plt.bar(df["作業者"], df["不良率"], color="orange")
plt.title("作業者別 不良率", fontproperties=jp_font)
plt.xlabel("作業者", fontproperties=jp_font)
plt.ylabel("不良率", fontproperties=jp_font)
plt.ylim(0, 0.15) # Y軸範囲調整(0〜15%)
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.xticks(fontproperties=jp_font)
plt.yticks(fontproperties=jp_font)
plt.tight_layout()
plt.show()
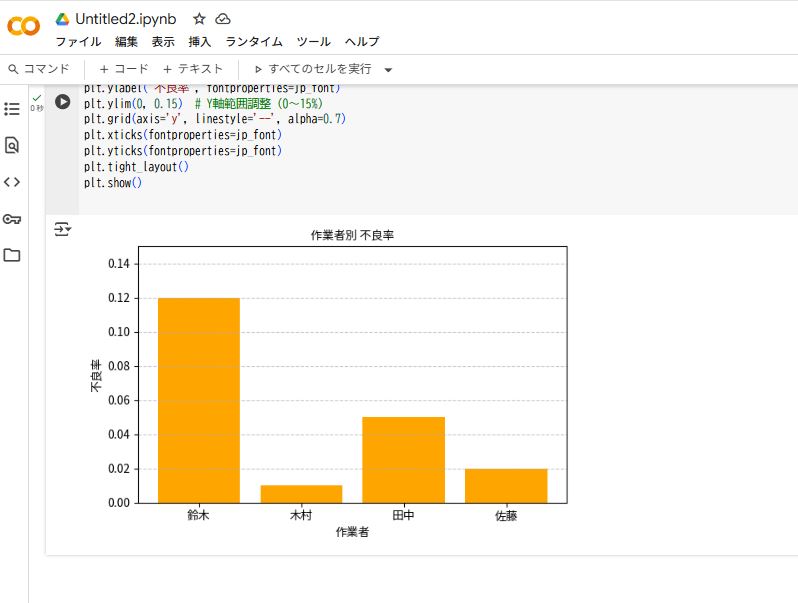
Google Colabで作成した層別グラフ
実務での活用事例①〜食品工場の異物混入
✔ 背景
食品工場で「異物混入」の件数が月によって増減していた。
✔ 層別条件
- 作業シフト(昼/夜)
- 作業者チーム(A班/B班)
- 製品種別
✔ ChatGPTへの棒グラフ作成 プロンプト指示例
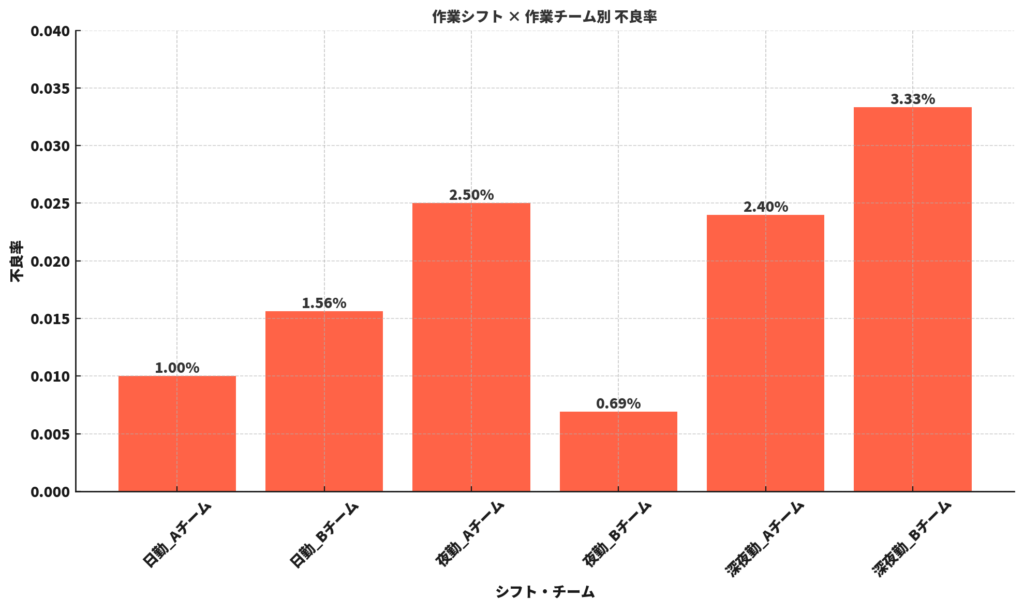
食品工場の異物混入データを基に「異物混入数 ÷ 作業数 = 不良率」 を用いて、作業シフト × 作業チーム の層別による 不良率の棒グラフ を作成する為のpythonコードを教えてください。フォントは Noto Sans Japanese を使用します。Pythonコード
# Google Colab利用時は以下を最初に実行してください
!apt-get -y install fonts-noto-cjk
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
# ▼ 異物混入データ(例:実データに置き換え可能)
data = {
"作業シフト": ["日勤", "日勤", "夜勤", "夜勤", "深夜勤", "深夜勤"],
"作業チーム": ["Aチーム", "Bチーム", "Aチーム", "Bチーム", "Aチーム", "Bチーム"],
"異物混入数": [3, 5, 7, 2, 6, 8],
"作業数": [300, 320, 280, 290, 250, 240]
}
df = pd.DataFrame(data)
# ▼ 不良率の計算(異物混入数 ÷ 作業数)
df["不良率"] = df["異物混入数"] / df["作業数"]
# ▼ 「作業シフト_作業チーム」を組み合わせて層のラベルにする
df["層"] = df["作業シフト"] + "_" + df["作業チーム"]
# ▼ Notoフォントの読み込み
font_path = "/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc"
jp_font = fm.FontProperties(fname=font_path)
# ▼ 不良率の棒グラフを作成
plt.figure(figsize=(10, 6))
bars = plt.bar(df["層"], df["不良率"], color="tomato")
# ▼ 数値ラベルを棒の上に表示(%形式)
for bar, rate in zip(bars, df["不良率"]):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height(), f"{rate:.2%}",
ha='center', va='bottom', fontproperties=jp_font, fontsize=10)
# ▼ グラフ装飾
plt.title("作業シフト × 作業チーム別 不良率", fontproperties=jp_font)
plt.xlabel("シフト・チーム", fontproperties=jp_font)
plt.ylabel("不良率", fontproperties=jp_font)
plt.ylim(0, max(df["不良率"]) * 1.2)
plt.xticks(rotation=45, fontproperties=jp_font)
plt.yticks(fontproperties=jp_font)
plt.grid(axis='y', linestyle='--', alpha=0.6)
plt.tight_layout()
plt.show()
✔ ChatGPTへの分析指示例
層別化した結果から作業シフト、作業者チーム毎に傾向を分析してください。✔ 発見
-
- 夜シフト×B班での発生が集中
- 原因:夜間のチェック体制が不十分
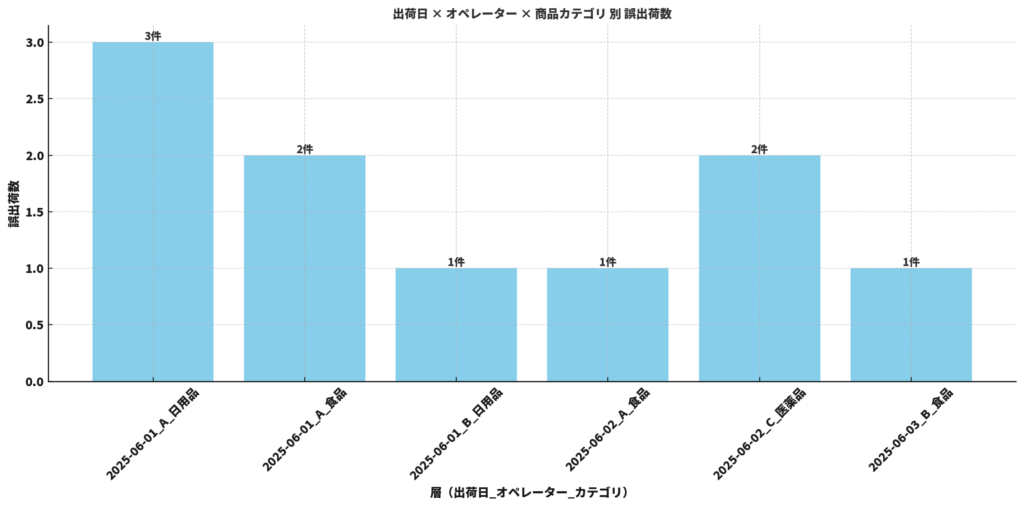
実務での活用事例②〜物流センターでの誤出荷
✔ 背景
誤出荷の件数が増加傾向。だが平均では大きな異常は見えない。
✔ 層別軸
-
-
- 出荷日(平日/土日)
- オペレーター名
- 商品カテゴリ
-
✔ ChatGPTへの棒グラフ作成 プロンプト指示例
物流センターでの誤出荷データをモデルに「出荷日 × オペレーター × 商品カテゴリ」の層別で集計し、棒グラフを作成してする為のPythonコードを教えてください。
Pythonコード
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
# ❶ 仮の誤出荷データ(例として使用。実データがある場合は差し替え)
data = {
"出荷日": ["2025-06-01", "2025-06-01", "2025-06-01", "2025-06-02", "2025-06-02", "2025-06-03"],
"オペレーター": ["A", "B", "A", "A", "C", "B"],
"商品カテゴリ": ["食品", "日用品", "日用品", "食品", "医薬品", "食品"],
"誤出荷数": [2, 1, 3, 1, 2, 1]
}
df = pd.DataFrame(data)
# ❷ 層の名称を「出荷日_オペレーター_カテゴリ」として結合
df["層"] = df["出荷日"] + "_" + df["オペレーター"] + "_" + df["商品カテゴリ"]
# ❸ 誤出荷数を層別に集計
grouped = df.groupby("層")["誤出荷数"].sum().reset_index()
# ❹ 日本語フォント(Noto Sans Japanese)のパスを指定
font_path = "/mnt/data/NotoSansJP-Black.ttf" # ← アップロード済みファイル
jp_font = fm.FontProperties(fname=font_path)
# ❺ グラフ描画
plt.figure(figsize=(12, 6))
bars = plt.bar(grouped["層"], grouped["誤出荷数"], color="skyblue")
# ❻ 数値ラベルを表示
for bar, val in zip(bars, grouped["誤出荷数"]):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height(), f"{val}件",
ha='center', va='bottom', fontproperties=jp_font, fontsize=9)
# ❼ グラフの装飾
plt.title("出荷日 × オペレーター × 商品カテゴリ 別 誤出荷数", fontproperties=jp_font)
plt.xlabel("層(出荷日_オペレーター_カテゴリ)", fontproperties=jp_font)
plt.ylabel("誤出荷数", fontproperties=jp_font)
plt.xticks(rotation=45, fontproperties=jp_font)
plt.yticks(fontproperties=jp_font)
plt.grid(axis='y', linestyle='--', alpha=0.6)
plt.tight_layout()
plt.show()
✔ ChatGPTへの分析指示例
層別化した結果から出荷日 、オペレーター 、商品カテゴリ毎に傾向を分析してください。✔ 発見と対策
-
-
- 土日の誤出荷率が高い
→ パート作業員比率が高い時間帯
→ 教育強化とWチェック導入
- 土日の誤出荷率が高い
-
層別化(Stratification)と全分散・外分散・内分散の関係
層別化と密接な関係にある「全分散・外分散・内分散」の考え方を、わかりやすく具体例を交えて解説します。
分散とは何か?まずは基本を押さえる
統計用語としての「分散」とは、データのばらつきの大きさを示す指標です。
数式で表すと、各データと平均の差を2乗し、それを平均したものです。
-
分散(variance) = Σ(データ − 平均)² / n
例えば、ある機械の製品重量にばらつきがあるとき、分散が大きいほど安定していないことを意味します。品質の安定性を評価する上で、分散は非常に重要な指標です。
層別化と分散の関係
全体データのばらつきを表す「全分散」は、内部要因と外部要因によるばらつきの合計と捉えることができます。
このとき、分散は次の3つに分けて考えられます:
| 名称 | 説明 |
|---|---|
| 全分散 | 全体データのばらつき(全体平均からのズレ) |
| 外分散 | 層(グループ)間のばらつき(グループ平均の違い) |
| 内分散 | 層(グループ)内でのばらつき(個体差) |
この3つの関係は、次の式で表現できます。
全分散 = 外分散 + 内分散
つまり、「全体のばらつき」は、「層の違いによるばらつき」と「層の中でのばらつき」を足したものと捉えることができます。
「全分散・外分散・内分散」を算出事例
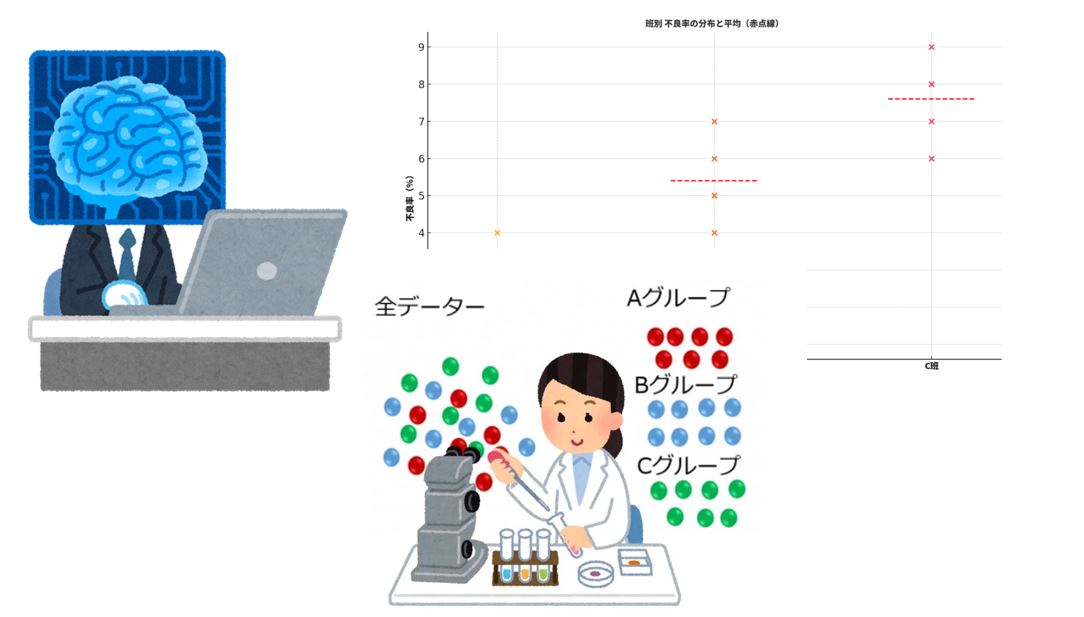
あるアイス工場で、3つの班(A班・B班・C班)があります。それぞれの班で1日5人ずつ不良率(%)を記録しました。
例題:アイス工場の不良率分析
あるアイス工場で、3つの班(A班・B班・C班)があります。それぞれの班で1日5人ずつ不良率(%)を記録しました。
各班のデータ(不良率%)
| 班 | 不良率データ |
|---|---|
| A班 | 2, 3, 1, 4, 2 |
| B班 | 5, 4, 6, 7, 5 |
| C班 | 8, 7, 9, 6, 8 |
ステップで理解する!
Step1:全データの平均(全体平均)
まず全部の値を足して人数で割ります。
A = [2, 3, 1, 4, 2]
B = [5, 4, 6, 7, 5]
C = [8, 7, 9, 6, 8]
全データ = A + B + C # 合計15人分
全体平均 = sum(全データ) / len(全データ)
= (2+3+1+4+2+5+4+6+7+5+8+7+9+6+8) / 15
= 85 / 15 ≒ **5.67**
Step2:全分散の計算
全分散 = 各データと全体平均の差の2乗の平均
全分散 = sum((x - 5.67)**2 for x in 全データ) / 15 ≒ 6.36
Step3:各班の「班内分散」(内分散)
各班ごとにばらつきを出して、平均する。
A班内の平均
A班内の分散
同様に…
- B班分散 ≒ 1.04
- C班分散 ≒ 1.04
3つの班の平均をとって:
Step4:外分散の計算
各班の平均値と全体平均の差を使います。
- A班平均 2.4
- B班平均 5.4
- C班平均 7.6
(n=各班の人数、N=全体の人数)
結果
| 指標 | 値 |
|---|---|
| 全分散 | 約 6.36 |
| 内分散 | 約 1.04 |
| 外分散 | 約 4.81 |
どう解釈する?
- 内分散が小さい → 班内ではみんな似たようなばらつき。
- 外分散が大きい → 班ごとの平均に大きな違いがある!
つまり、「誰が悪いというより、班によって仕事の出来がバラバラ」ってこと!
応用のヒント(初心者向け)
この考え方は、次のような場面で使えます:
| シーン | 活用例 |
|---|---|
| 工場の不良率 | 班別・日別・機械別などで「どこに差があるか」見える化 |
| 接客評価 | 支店ごとのサービスの差を見る |
| 学力分析 | 学年別・クラス別で学力の差を見る |
3つの分散を1行で!
全分散 = 外分散 + 内分散
👉 どれだけの「ばらつき」が「グループ間」か「グループ内」かを分解できる!
Pythonコード
アイス工場の不良率データを使って、「全分散・内分散・外分散」をPythonで計算するコードをわかりやすく紹介
アイス工場:不良率データ
# 各班の不良率データ
A班 = [2, 3, 1, 4, 2]
B班 = [5, 4, 6, 7, 5]
C班 = [8, 7, 9, 6, 8]
# グループまとめ
groups = {
'A': A班,
'B': B班,
'C': C班
}
分散を求めるコード(ステップ別)
import numpy as np
# 全データ
all_data = A班 + B班 + C班
N = len(all_data)
group_size = len(A班)
# 全体平均
overall_mean = np.mean(all_data)
# 全分散(不偏分散じゃなく母分散)
total_variance = np.mean([(x - overall_mean)**2 for x in all_data])
# 内分散:各班内の分散を求めて平均
within_variances = []
for班名, data in groups.items():
group_mean = np.mean(data)
group_variance = np.mean([(x - group_mean)**2 for x in data])
within_variances.append(group_variance)
within_group_variance = np.mean(within_variances)
# 外分散:班の平均と全体平均の差
between_group_variance = np.mean([
(np.mean(data) - overall_mean)**2 for data in groups.values()
]) * group_size / N # 重みづけ必要
# 結果表示
print("■ 全体平均:", round(overall_mean, 2))
print("■ 全分散:", round(total_variance, 2))
print("■ 内分散(班内):", round(within_group_variance, 2))
print("■ 外分散(班間):", round(between_group_variance, 2))
print("■ 全分散 ≈ 内 + 外:", round(within_group_variance + between_group_variance, 2))
出力結果(参考)
■ 全体平均: 5.67
■ 全分散: 6.36
■ 内分散(班内): 1.04
■ 外分散(班間): 4.81
■ 全分散 ≈ 内 + 外: 5.85 ← 誤差は丸めによるもの
分散比(F値)による統計的な検定も可能
品質管理の現場では、分散分析(ANOVA)という手法で統計的に検定を行うこともあります。
これは、外分散 ÷ 内分散 = F値 を算出し、
-
F値が大きい ⇒ 層による差(外分散)が支配的
-
F値が1に近い ⇒ 層ごとの差はあまりない(内分散が主)
というふうに判断できます。
このような数値的根拠を使えば、「どの層が原因か」を客観的に説明でき、改善の方向性を明確にできます。
現場で使うときのポイント
-
層を切る軸を明確にすることが第一歩(オペレーター・設備・時間帯など)
-
データをグループごとに分類するだけでなく、層ごとの平均・分散を必ず見る
-
外分散が大きければ「層による差」、内分散が大きければ「層の中のばらつき」を対策
-
グラフ(箱ひげ図、棒グラフ、散布図)で可視化すると、関係者に共有しやすい
まとめ 層別と分散の組み合わせは、改善の起点になる
層別は、「全体をただ見るだけでは見えない違い」を浮き彫りにする力があります。そして、分散という統計的な見方を加えることで、その違いが偶然か、必然かまで見えてきます。
「層別 + 内分散・外分散の分析」を繰り返すことで、現場のムダ・ムラ・ムリの原因を可視化し、再発防止や品質向上に大きく貢献することができるのです。
-
-
- 層別化は「見えない真因を可視化するための入口」
- ChatGPTは「気づきを与える対話パートナー」
- データ×AIによって、品質改善のPDCAサイクルが加速
-
*noteに「AIによる層別化の成功事例」を投稿しました、参照願いします。






















コメント