“はかる”とは? | 計測計量士の資格試験キーワード
“はかる”という言葉の意味は下記のような意味である。
| 言葉 |
意味 |
備考 |
| はかる |
仕上げようと予定した作業の進捗状態を数量、重さ、長さについて見当をつける |
広辞苑より |
|
(計・量・測)物の数量、または時間の度合を一定の単位と比較して確かめる,秤、枡(ます)、ものさし、時計などの計器で測定する。 計量、計算する。 |
日本国語大辞典より |
|
| 計測 |
器械を使って、数、量、長さ、重さなどをはかること。 |
|
| 計量 |
長さや重さなど物の数量をはかること。分量、目方をはかること。 |
|
| 測定 |
計器や装置を用い、ある現象を特徴づける数量を読みとること。 |
|
| 度量衡 どりょうこう |
長さと体積と重さ。 |
JISでは上記の言葉の定義をはっきりさせる為に下記のように定義している。
|
用語 |
定義 |
備考 |
|
計測 |
特定の目的をもって事物を量的にとらえる為の方法、手段を研究し実施しその結果を用い所期の目的を達成させること。 備考: 公的に取り決めた測定標準を基礎とする計測を計量ということがある |
JIS Z 8103 |
|
測定 |
ある量を基準として用いる量と比較し数値または符号を用いて表すこと。 |
JIS Z 8103 |
また、JIS 8103では計測に関した言葉についても下記の様に定義している。
| 用語 |
定義 |
| かたより |
測定値の母平均から真の値を引いた値 |
| ばらつき |
測定値のおおきさがそろっていないこと。 または不揃いの程度 |
| 測定値 |
測定によって求めた値 |
| 正確さ |
かたよりの小さい程度 備考:推定したかたよりの限界の値で表した値を正確度 |
| 精密さ |
ばらつきの小さい程度 備考:ばらつきを標準偏差またはその指定した倍数で表した値を正確度 |
| 精度 |
測定値の表す値または測定結果の正確さと精密さを含めた総合的な良さ |
| 誤差 |
測定値から真の値を引いた値 |
| 真度 |
真の値からのかたよりの程度 |
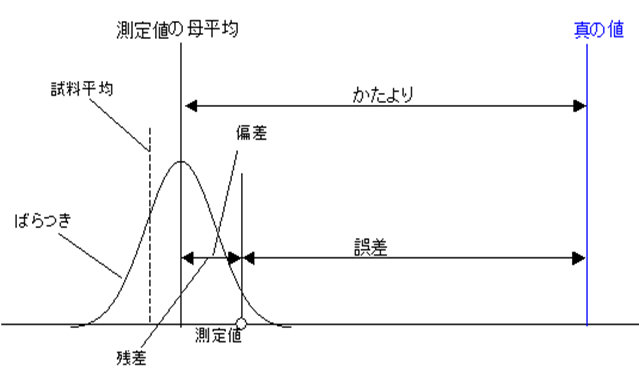
計測計量の概要
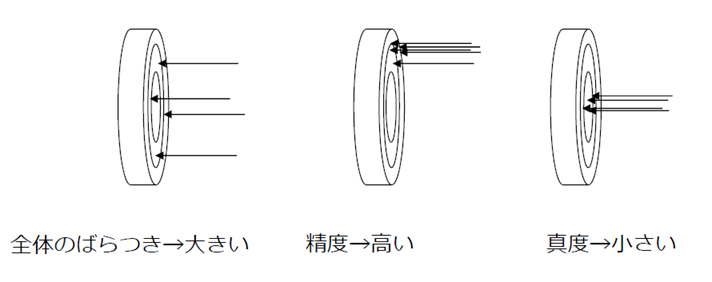
計測計量のバラツキ、精度、真度の解説
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
計測管理 「計測活動の体系を管理すること.」 (Z 8103)
計測の意味が広範でかつ計量との区別があいまいであることから計測管理も広範の管理を意味する.
実際には品質管理の一部あるいは独立したものとして生産技術全体を支えるための仕事で,特にデータを数量化するのに不可欠のものである.
計測器の管理だけでなく,計測データの管理,計測の組織体系全体の管理を行う.
計測 measurement, instrumentation
「特定の目的をもって,事物を量的にとらえるための方法・手段を考究し,実施し,その結果を用い所期の目的を達成させること.」(Z 8103)
計測と計量とは意味が同じか,どちらが広義かという議論は,関係者の間ではしばしば行われている.歴史的には計量のほうが古いといわれるが,計量法という法律に関係して,計量のほうが固苦し く,古くさいという印象をもつ人もいる.
一方,計測のほうは品質管理とは対置的だが,計量の中には製品の量目など,品質項目を含むために,計量のほうが品質管理に近いと考える人もいる.
実体としては計測も計量も大差はない.
計量 metrology
公的に取り決めた測定標準を基礎とする計測 (Z 8103)
引用先:クォリティーマネジメント用語辞典 日本規格協会
関連用語:計測管理
単位とは? | 長さ、重さ、量の基準
国語辞典で調べると単位は下記の意味である。 長さ、重さ、量などの数量を計算するときの基準となるもの。 また、その数値。長さのメートル、重さのグラムなどの類。
“はかる”ということは同じものを複数つくる必要があってはじめて必要になるもので自分で全てのものを つくり、使用していた場合は必要ではない。 長さ、重さ、容積の物々交換が発達するまでは無用なものであった。
物つくりの分業体制ができるようになって必要となった道具であり、他の品物と比較することができる 便利な道具である。 はかることの基準はどこの国でもはじめ人間自身の体の大きさを持って決めていた。
長さの最初の基準は身体の一部だった。古代オリエント時代の単位は,腕の長さから,キュービットが使われ, ヤードの基本となった。インチやフィートもそれぞれ指や足の大きさに起因すると言われている。
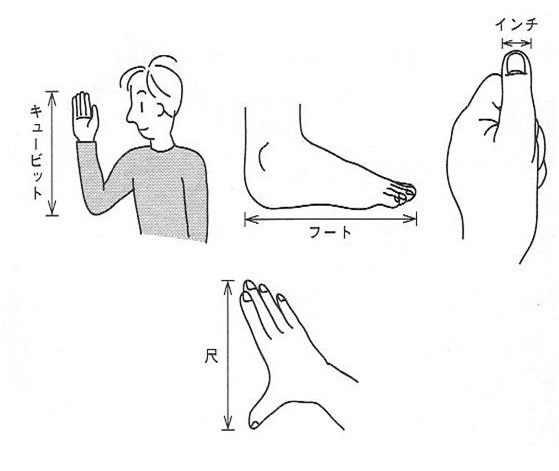
尺、インチやフィートの起源
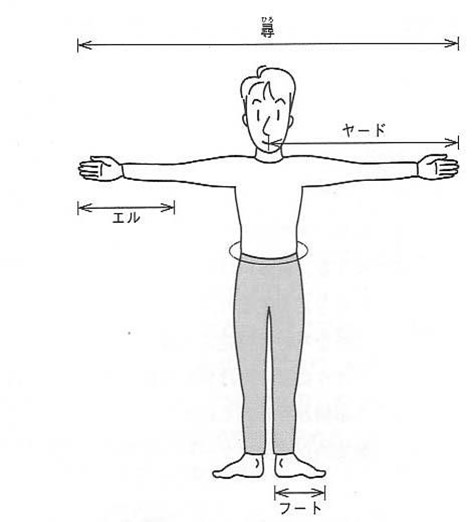
尋、 ヤードの起源
現在の単位の基準
【長さの基準】 1mの定義
メートル原器 光の速さ(真空中)を基準
「地球の子午線の赤道から北極までの100万分の1」と決めたのが最初です(メートル原器作成)
↓
1960年: 86Kr原子のだいだい色スペクトルの真空中における波長の1650763.73倍を1メートルとする。
↓
1983年: 光の速さ(真空中)を基準にするようになった。
【質量の基準】 1Kgの定義
1790年、質量の基本単位「キログラム」は「約4℃で最大密度にある純水の1デシ立方メートル(1辺が10cmの立方体)の質量」と定義され、その後これに基づき、白金90%、イリジウム10%の合金製で、直径39mm・高さ39mmの 円柱形の「国際キログラム原器」が作られました。
この国際キログラム原器はフランスの国際度量衡局に保管され、これと同形状・同材質のキログラム原器が40個作られ、世界各国に配られ、それぞれの国の質量単位のモトとなるキログラム原器となったのです。
日本のキログラム原器は№6で、現在、茨城県つくば市の通商産業省工業技術院計量研究所に保管され約30年ごとに故郷であるパリ郊外の国際度量衡局の国際キログラム原器と比較され、値付けされています。
キログラム原器

キログラム原器
【時間の基準】
「1日を24等分したものが1時間。1時間を60等分したものが1分。1分を60等分したものが秒」
↓
1967年:セシウム133の特定放射の9192631770周期分の時間

セシウム133の特定放射の9192631770周期分の時間
【温度の基準】
セッ氏温度(セルシウス温度) 単位記号:℃
(「摂氏」はスウェーデン人セルシウス(A=Celsius)の中国語表記「摂爾思」から)温度を計る単位の一つ。
一気圧における水の氷点を零度、沸点を一〇〇度とし、その間を一〇〇等分した温度目盛り。
氷点以下や沸点以上の温度も同じ目盛り間隔にしてある。記号℃一七四二年、セルシウスが提唱した。
1990年に定められた温度定義では、17個の温度定点が与えそれを元に基準をきめている。
変更理由:
零点、沸点の値が不変的でないために変更を行った。例として、1990年での「1気圧下の水の沸点は、約99.974℃であり現在の温度目盛りでは、水の沸点は100℃ではない
絶対温度(ケルビン温度)単位記号:K 呼び名:ケルビン
摂氏マイナス二七三・一六度を零度とし、摂氏と同じ温度単位をもつ温度系、記号/ ゼロ/の温度では物質を構成する原子分子の熱振動はすべて静止する。従ってゼロ/以下の温度は存在しない。
華氏温度(セルシウス温度) 記号:°F
「華氏」はドイツ人ファーレンハイト(G.D.Fahrenheit)の中国語表記「華倫海」から)温度をはかる単位の一つ。水の氷点を三二度、沸点を二一二度とし、その間を一八〇等分した温度目盛り。一七一四年、ファーレンハイトが制定。ヤードポンド単位系で用いられる。
SI単位系 | メートル , キログラム , 秒 , アンペア , ケルビン , モル , カンデラ
SI (System International unite) 国際単位系、度量衡の標準単位系で、旧[MKS]単位系をもとに、次のような単位を基本として組み立てた単位系のこと。1960年に国際度衡量総会で採択された。
・SI基本単位:
| 量 | 名 | 記号 | 定 義 |
| 長さ | メートル | m | メートルは,1/299 792 458秒の時間に光が真空中を伝わる行程の長さ |
| 質量 | m | kg | キログラムは質量の単位で,国際キログラム原 器の質量 |
| 時間 | 秒 | s | 秒は,セシウム133の原子の基底状態の二つの 超微細準位間の遷移に 対応する放射の9 192 631 770周期の継続時間 |
| 電流 | アンペア | A | アンペアは,真空中に1m間隔で平行に置かれた ,無限に小さい円形断面の 無限長の2本の直線導体のそれぞれを流れ,この導体1メー トルごとに 2×10-7ニュートンの力を及ぼし合う不変電流 |
| 熱力学 | ケルビン | K | ケルビンは,水の三重点の熱力学温度の1/ 273.16の温度 |
| 物質量 | モル | mol | モルは,0.012キログラムの炭素12の中に存在 する原子の数と等しい数 の構成要素を含む系の物質量 |
| 光度 | カンデラ | cd | カンデラは,周波数540×1012ヘルツの単色放 射を放出する光源の, 放射強度が1/683ワット毎ステラジアンである方向の光度 |
・SI 補助単位:ラジアン , ステラジアン

SI 補助単位:ラジアン , ステラジアン
・基本単位を用いて表現されるSI 組立単位の例:
平方メートル , Kg毎立方メートル , メートル毎秒 , 毎平方メートル , 毎ケルビン , モル毎立方メートル , 毎平方メートルカンデラ
| 量 |
名称 |
記号 |
| 面積 | 平方メートル |
m2 |
| 密度 | Kg毎立方メートル |
kg/m3 |
| 速さ | メートル毎秒 |
m/s |
| 電流密度 | 毎平方メートル |
A/m2 |
| 線膨張係数 | 毎ケルビン |
K-1 |
| モル濃度 | モル毎立方メートル |
mol/m3 |
| 輝度 | 毎平方メートルカンデラ |
cd/m2 |
・固有の名称をもつSI 組立単位:
ヘルツ、ニュートン、パスカル、ジュール、ワット、クーロン、ボルト、ファラド、オーム、ウエーバ、テスラ、ヘンリー、セルシウス度、ルーメン
| 量 |
名称 |
記号 |
|
| 周波数 |
ヘルツ |
Hz |
|
| 力 |
ニュートン |
N |
|
| 力 |
パスカル |
Pa |
N/m2 |
| エネルギー、仕事 |
ジュール |
J |
N・m |
| 射束 |
ワット |
W |
J/s |
| 電荷 |
クーロン |
C |
|
| 電圧,起電力 |
ボルト |
V |
W/A |
| 静電容量 |
ファラド |
F |
W/A |
| 電気抵抗 |
オーム |
Ω |
V/A |
|
S |
A/V |
||
| 磁束 |
ウエーバ |
Wb |
V・s |
| 磁束密度 |
テスラ |
T |
Wb/m2 |
| タンス |
ヘンリー |
H |
Wb/A |
| 温度 | セルシウス度 |
℃ |
|
| 光束 |
ルーメン |
lm |
|
| 照度 |
ルックス |
lx |
lm/m2 |
・SI 接頭語:
SI 単位の量の種類によっては,単位の大きさが常用される大きさと比較して極めて大きい量や小さい量が 発生する。このため,10の整数乗倍で表せるように,SI 接頭語を定めてある。
エクサ , ペタ , テラ , ギガ , メガ , キロ , ヘクト , デカ , デシ , センチ , ミリ , マイク , ナノ , ピコ , ファト , アト
| 単位 |
名称 |
記号 |
| 10 18 |
エクサ |
E |
| 10 15 |
ペタ |
P |
| 10 12 |
テラ |
T |
| 10 9 |
ギガ |
G |
| 10 6 |
メガ |
M |
| 10 3 |
キロ |
k |
| 10 2 |
ヘクト |
h |
| 10 |
デカ |
da |
| 10-1 |
デシ |
d |
| 10-2 |
センチ |
c |
| 10-3 |
ミリ |
m |
| 10-6 |
マイク |
μ |
| 10-9 |
ナノ |
n |
| 10-12 |
ピコ |
p |
| 10-15 |
ファト |
f |
| 10-18 |
アト |
a |




















コメント