層別の作り方について下記の点をポイントに図解入れで解説しています。
・層別化の方法、使い方
・層別化のテンプレート エクセル
・層別化 製造事例
・層別化 統計学
モノづくりの参考になれば幸いです。(*^_^*)
2024年版 簡単 分かり易い 層別化とは? 活用事例 統計解析 【音声解説】
QC7つ道具の層別についての紹介動画です。
3分で分かる! 層別化とは 概要解説
層別化とは、ある集団を、特定の特性(性別、年齢、疾患のタイプなど)に基づいて、いくつかのより小さなグループ(層)に分けることです。この手法は、様々な分野で活用されており、特にデータ分析や実験計画において重要な役割を果たしています。
層別化の目的
異質性の発見: 集団全体で見ると隠れてしまう、それぞれの層が持つ特徴や傾向を明らかにする。
分析の精度向上: 層ごとに分析することで、より詳細な情報を得ることができ、より正確な結論を導き出すことができる。
効果的な対策の立案: それぞれの層に合わせた対策を講じることでより効果的な結果が期待できる。
層別化の例
医療分野: 患者を性別、年齢、病状のステージなどによって層別化し、最適な治療法を選択する。
マーケティング分野: 顧客を年齢層、性別、購入履歴などによって層別化し、ターゲットに合わせた商品やサービスを提供する。
社会調査: 人口を地域、職業、学歴などによって層別化し、社会現象の要因を分析する。
層別化の種類
単純な層別化: 1つの変数に基づいて層別化を行う。
複合的な層別化: 複数の変数を組み合わせて層別化を行う。
層別化のメリット
「全体の姿と小さな姿の比較が視覚化できる」ということです。層別できるようになると、データの塊にしか見えなかったものが、具体的な問題を示す意味ある数字として見えてくるようになります。
大きく・曖昧な問題を細かく分けて、より具体的な一つ一つの問題に整理することができるので、問題解決では必ず活用する手法です。
層別化の注意点
層の数が多すぎると、分析が複雑になる。
各層のサンプル数が少なすぎると、統計的な信頼性が低下する。
層別化の基準となる変数の選択が、分析結果に大きな影響を与える。
*AI chatGPTで層別解析するには下記の記事が参考になります。

層別解析とは
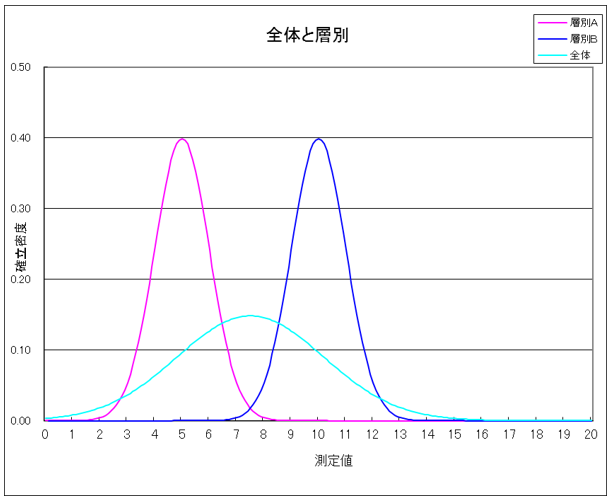
層別化とは、たくさんのデータを、その得られたデータの特徴によって、グループ分けすることをいいます。たとえば、いくつかの機械で加工した部品のある特性値のバラツキが大きい場そのバラツキの原因を調べるためにデータをその得られた特徴である、機械や作業者別にグループ分けすることをいいます。
そして層別を使用して原因の調査を行い分析、解析することを層別解析といいます。
生物学のイネ科タイプの生産構造図、広葉タイプの生産構造図を測定する為の層別刈取法 にも用いられています。
英語:stratified analysis
中国語:数据分层法
QC 層別 エクセル テンプレート
下記にエクセルで作成した層別表があります。
平均値および標準偏差だけを入力すれば全体とロットのバラツキ度合いが一目でわかる正規分布表(下図)を作成しました。
ご自由にダウンロードしてご使用ください。
正規分布 比較表
層別 と 分類 違い
分類とは、あらかじめ用意されたカテゴリーに従って試料を仕分ける方法および行為なので、層別とは似ているが同じ意味ではない。
*層別:
。データを年齢別などの同じ共通点を持つグループに分類すること。層別に分けることで、漠然としたデータの特徴がはっきりする。
層別 相関
ふたつのX,Y変数データーの相関を調査する場合、データーを初めに層別しないと相関がわかりません。これは相関だけでなくヒストグラム分析、グラフ解析をするときにも言えることです。
優れた統計分析、解析手段があって元のデーターが正しく層別されないと正しい解析、分析はできません。
ヒストグラムの層別
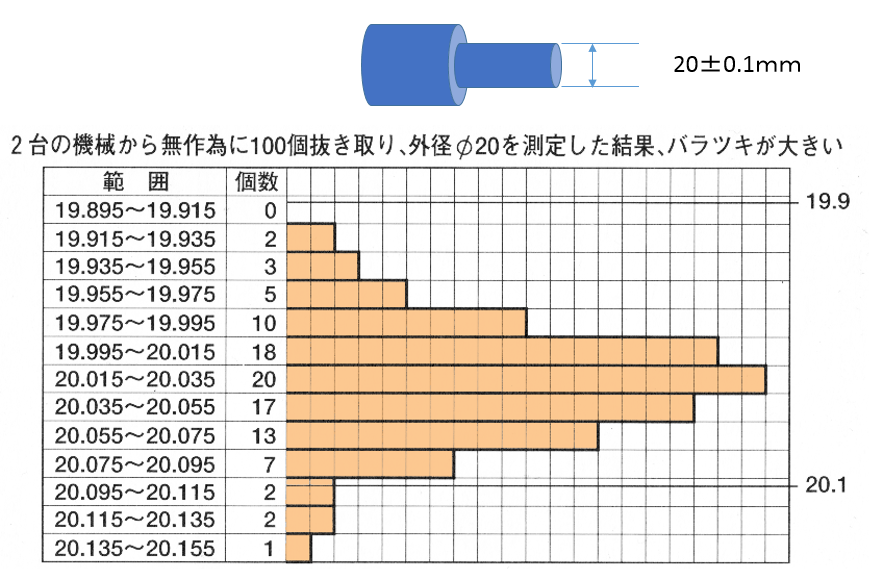
たとえば、2台の機械で図1の部品を加工しています。無作為に100個を抜き取り、外径を測定し、ヒストグラムを作成したところ、図1のようにバラツキが大きいことがわかりまし
た。
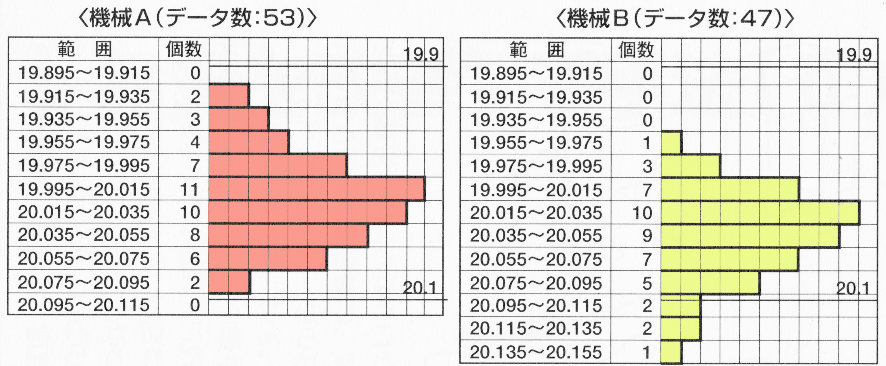
原因を調べるため、データの特徴である機械A、機械Bにデータをグループ分け(層別)し、ヒストグラムを作成したところ図2のような結果が得られ、バラツキの大きな原因が機械Bにあることがわかります。
層別化サンプリング、層別抽出法
サンプルを規定のルールに沿って層別するサンプリングを層別化サンプリング、層別抽出法と呼びます。
このように、層別する前後のデータを比較することによって、データの性質を把握し、対策につなげていくことができます。
層別で大切なことは、データの特徴を捉えてグループ分けすることです。
製造工場などでよく行なわれる層別には、次の項目があります。
①時間別・・午前・午後、昼夜、曜日など
②作業者別・・個人、男女、年齢、経験年数、技能など
③材料別・・メーカー、購人先、ロット、購入時期など
④機械別・・機種、号機、型式など
⑤方法別・・作業方法、口ットなど
⑥条件別・・温度、湿度、作業速度、作業場所など
⑦検査測定別・・検査員、測定者、測定器、試験機、測定場所など
関連記事:統計的サンプリングとは?
層別解析 活用の仕方は?
層別には、いろいろな活用の仕方がありますが、前述のようにデータのバラツキの原因を調査し、データのバラツキを小さくし、不適合品の発生を少なくするなど、不適合品の原因究明や作業改善を行なうために活用することができます。
層別は、異なる層の間の分布の違いや、層の中での分布を調べて、ばらつきの原因を探るために役立ちます。特に、パレート図、ヒストグラム、散布図、管理図などと合わせて活用すると効果的です。ただデータをたくさん集めただけでは、真の原因を探し出して、その原因に対する適切な処置を決めることは難しいです。
問題を検討する場合、製造する機械によって特性に差がないか、原材料によって差がないか、人、設備によって差がないかなどを考え、データを分けてグラフ化するなどの処理をして、分けたものを比べることで、問題の原因などの手がかりが把握できます。
なお、層別に似たものに「分類」という用語があります。分類とは、「あらかじめ用意されたカテゴリーに従って試料を仕分ける方法及び行為。ですので、層別と混同して使用しないようにして下さい。
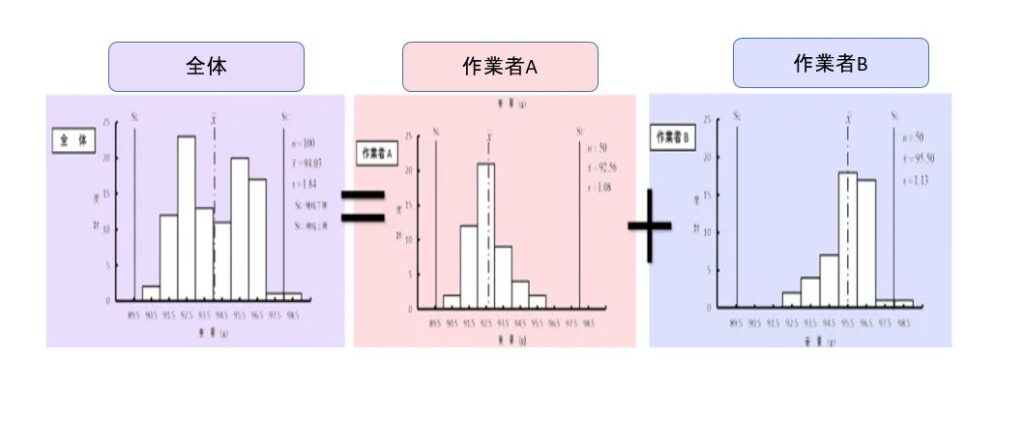
図3 では、全体のヒストグラムが二山形で上限規格(SU)を超えているものがあることから、作業者ごとに層別してヒストグラムを作成したものです。層別したところ、作業者 A は規格を満たしていますが、平均は下限規格(SL)の方に偏っていること、作業者 B は平均が上限規格の近くにあって、上限規格を超えているものがあることがわかります。
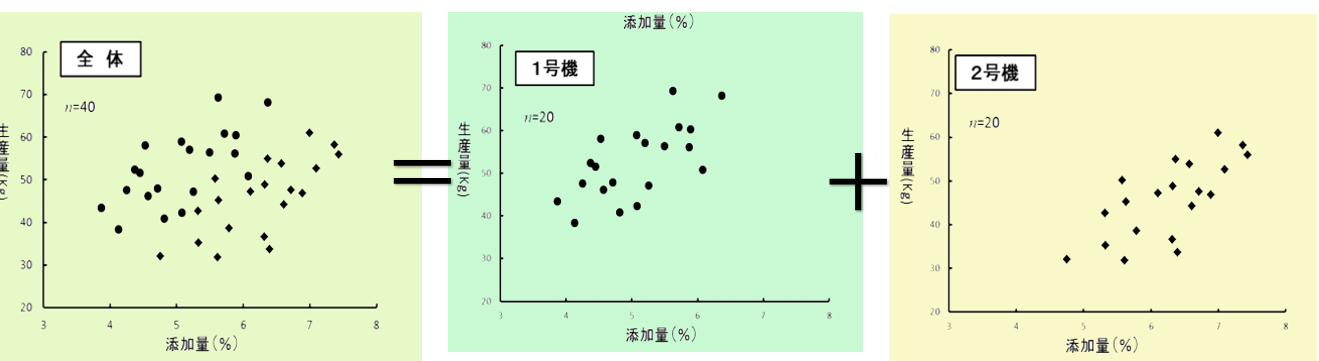
図 4 の全体の散布図は 2 台の機械で製造した結果を示したものです。全体の散布図では、添加量と生産量との間に相関があるか不明瞭ですが、機械毎に散布図を作成してみると、どちらの機械も添加量と生産量の間には正の相関があることが明確になります。
関連記事:QC七つ道具
エクセルでの層別散布図の作り方
データーを層別しないと散布図を作成しても相関が見えない場合がよく発生します。
ここでがエクセルを使用して層別散布図を作成します。
データー収集
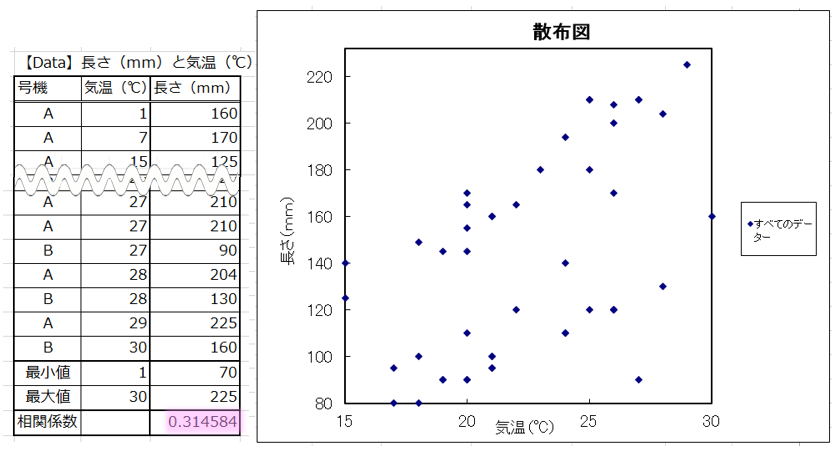
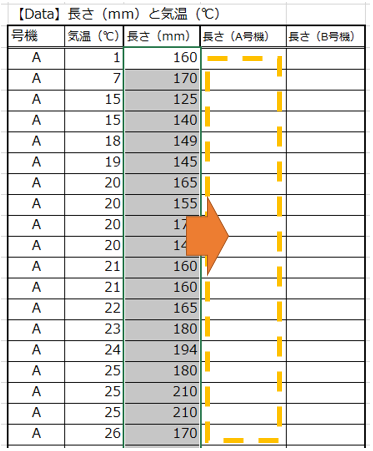
部品Zの気温と長さを測定した結果が下記の表になりました。
相関係数は0.31と相関なしの結果でした。
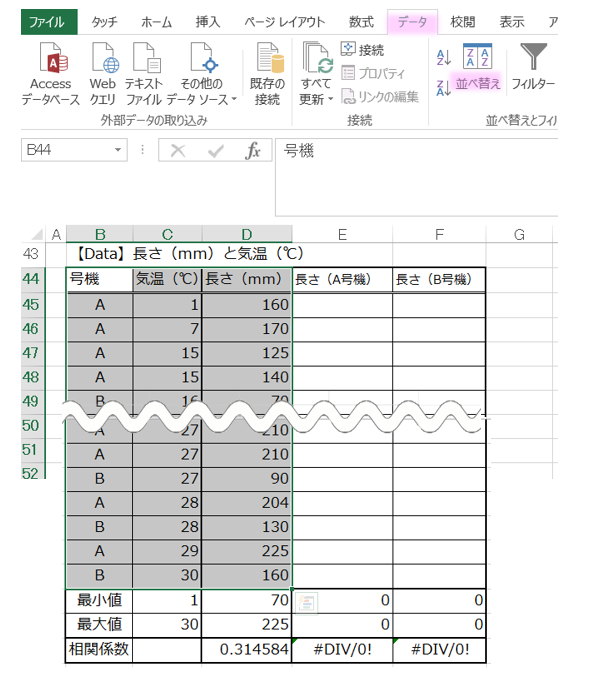
A号機&B号機別 層別欄 追加
そこで製造機械別(号機別)を層別をして再度、散布図を作成する事にし、はじめに表にA号機、B号機のデーターが入力できるように欄を追加しました。
号機別 並び替え
次に号機別の並べ替えを行います。
はじめに並べ替え範囲(グレー色範囲)をマウスで選択。
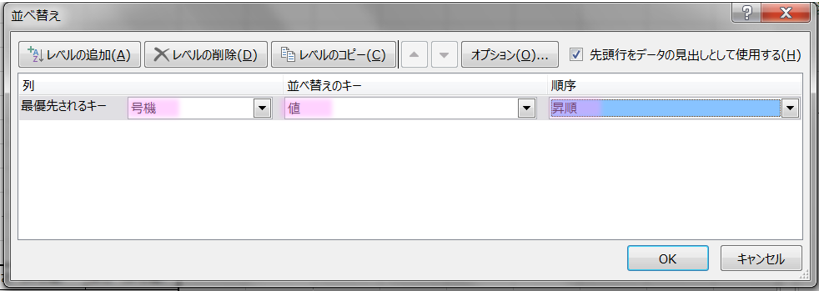
次はデータータグ→並べ替えを選択します。
次に下記のダイヤログが表示されるので下記のように設定します。
最優先されるキー:号機 並べ替えのキー:値 順序:昇順
最後にOKを選択して並べ替えを行います。
A号機&B号機データーの移動
並べ替えが終了したA号機データーをまとめて新規に作成した長さ(A号機)に移動します。
同様にB号機のデーターも移動します。
データーの選択
次にA号機及びB号機データーをグラフに反映することができるようします。
デザインタグ→データーの選択→凡例項目(系列)の追加を選択します。
系列の編集
系列の編集ダイアログが開きます。系列名に 1 つ目のグループの名称を=”A号機”
という形式で入力し、つづけてA号機の X(第 1 変数)の値の範囲、Y(第 2 変数)の値の範囲を指定していきます。
最後にOKボタンをクリックします。
同様にB号機についても同様な編集を行います。
エクセル 層別散布図の完成
最後に元データーを削除しその凡例”すべてのデーター”も併せて削除します。
凡例の削除は該当の凡例を選択後にDELキーで削除してください。
層別 統計学
層別 平均の関係
層別する前の全体の平均値と層別後の各ロット平均値には下記のような関係がある。
層別後のサンプル数: N1,N2,N3・・・・・Nk
各層別ロットの平均値: μ1,μ2,μ3・・・・μk
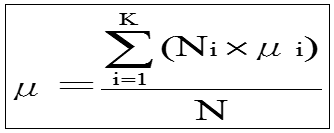
全平均=層別ロットの平均の平均
層別 外分散 | σb2
層別された各ロットの平均値を層別ロットのサンプル数をウエィトにした時,層別ロットの分散を外分散といい普通σb2で表わせられる。
層別後のサンプル数: N1,N2,N3・・・・・Nk
各層別ロットの平均値: μ1,μ2,μ3・・・・μk
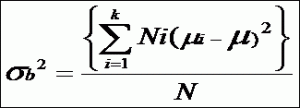
外分散計算式
外分散=層別ロットの平均の分散
層別 内分散 | σw2
層別されたロット内の分散をその層別ロットの大きさをウェイトにして全層別ロットに亘って加重平均したものを内分散といい普通σw2で表わせられる。
層別後のサンプル数: N1,N2,N3・・・・・Nk
各層別ロットの分散: σ1,σ2,σ3・・・・σk
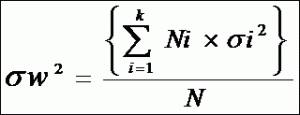
内分散計算式
内分散=層別ロットの分散の平均
層別 全分散、外分散、内分散の関係
層別される以前の集団を全集団といい、その分散を全分散といいます。
ひとつの集団をいくつかの層別ロットに分けると外分散σb2、内分散σw2が生じ全分散との関係は下記の式のようになる。
![]()
上記の式は全分散が外分散と内分散に分けられることを示している。
層別 分散比
全集団の分類をなるべく類似なものが集まる意図を持って分類(層別)すると外分散σb2は大きく内分散σw2は小さくなる。
一方、何らかの意図もなくランダムに分類した場合は元の集団の大きさ(N)が分割数(K)に比べてはるかに大きければ外分散σb2は小さく内分散σw2は大きくなり全分散σ2と差があまり見られなくなる。
この性質を利用してすでにある意図をもって分類されたと思われる集団に対して外分散σb2、内分散σw2を計算して全分散σ2、内分散σw2を計算して全分散σ2との関係を見ればその分類効果を実証的に評価(外分散σb2が大きいほど分類効果あり)することができる。
また、いくつかの集団の類似性を見たいときはその集団の外分散σb2、内分散σw2、全分散σ2を見ることによって各集団の類似性を評価することができる(外分散σb2が小さいほど類似性がある)
これらの考え方は実務的に大変役に立つものである、分類効果をみるためのひとつの尺度としては下記式がある。
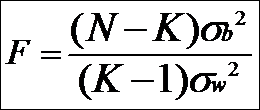 N:全体の大きさ
N:全体の大きさ
K:分割の数
類似のものを集めて分割した場合
Fの値は1よりおおきくなり、分類効果があるほど大きくなる。

層別分析
ランダムにサンプルして分割した場合
Fの値は1に近い値となる
各分割ロットの平均値の差がないように分類した場合
Fの値は1より小さくくなり、分類効果がないと判断される。
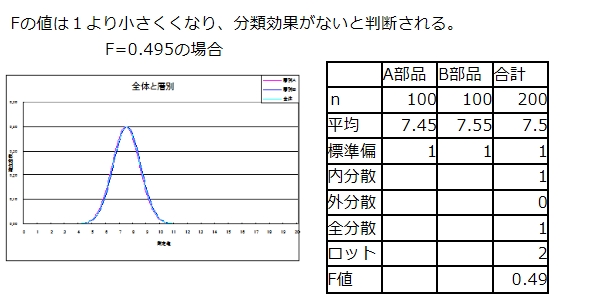
層別分析
まとめ
層別化は、複雑なデータをより深く理解し、効果的な対策を立案するための重要な手法です。様々な分野で活用されており、データ分析の基礎的な知識として身につけておくべきものです。
関連キーワード:
#層別化分析
#層別化サンプリング
slideshare スライドシェア 無料ダウンロード資料(PDF)
パワーポイントで作成したスライドシェア資料です。


























コメント