- 回帰分析 regression analysis 【イラスト図解】
回帰分析 regression analysis 【イラスト図解】
英語:regression analysis 中国語:回归分析
回帰分析とは
原因と結果の関係を図、数式によって求め分析していく方法。
応答変数に説明変数を結びつけるモデルを評価するための手続きの集まり。(Z 8101-3)
「回帰」という概念は19世紀末に生物統計学者カルトン(F.Galton)によってはじめて用いられた。
彼は親子の身長の測定値を見て背の高い親をもつ子の平均身長は親ほど高くなく,背の低い親をもつ子の平均身長は親ほど低くないことに気づき第2世代は平均の方向に「回帰」すると考えた。
これ以来ふたつの(確率)変量X,Yについて,Xを与えたときのyの期待値をyのXの上への回帰(関数)と呼ぶようになった。
現在では,このような歴史的経緯とあまりかかわりなく,応答変数yの期待値が説明変数(x1…xp)と未知母数ベクトルθ,既知の関数fを用いて
E(y)=f(x1…,xp;θ) (1)
と書けるとき,yと(x1,…,xp)の間には回帰関係があると呼ばれる。
現象の定量的な理解やyの予測のため,有効な回帰モデル(1)を構築することが回帰分析の主要な目的であるが,そのためには,必要にして十分な説明変数を選択し,適当な関数形を定める必要がある。また,モデル検証のためにyの実現値と予測値との残差を調べる残差分析や式(1)では表しきれない特異な外れ値やパラメータ推定に大きな影響を与える観測値を検出する回帰診断も,回帰分析の重要な過程である。
特に,説明変数がX一つであり,平均Oの誤差項εを用いて
y=β0+β1X十ε (2)
と書ける場合を単回帰分析,同様に
y=β0十β1×1十‥βpxp十ε (3)
と書ける場合を重回帰分析と呼ぶ。
式(2)や式(3)は線形モデルの一種であり,パラメータ推定には,普通,最小二乗法が用
いられる。β0を定数項,βiを(偏)回帰係数,式(2)のβ0+βiXを回帰直線,式(3)
のβ0+β1X1+…+βpxpを回帰平面と呼ぶ。
引用先:クォリティーマネジメント用語辞典 日本規格協会
回帰分析の種類
回帰分析とは、調べたいデータの項目(変数)の間の関係性を数式で表現することで、現状把握を行ったりある変数から他の変数の値を予想したりする統計学の分析手法になります。
代表的なものとして、回帰分析には3つの種類があります。
単回帰分析:1つの説明変数が1つの目的変数を導くとき、それを分析することを単回帰分析という。 例として子供の自転車の上達度という結果(目的変数)は、練習した時間に大きな影響を受けるので、要素(説明変数)が1つしかないと想定して単回帰分析で分析する。
重回帰分析:二つ以上の量的な説明変数から、一つの目的変数を予測する手法。 たとえば、接客の質や品数、売場面積などを変数とした小売店の売上などを予測するといった分析です。
ロジスティック回帰分析:目的変数が0と1からなる2値のデータ、あるいは0から1までの値からなる確率などのデータについて、説明変数を使った式で表す方法、ある事象が起こる確率を予測することができます。
回帰分析で何がわかるのか? 事例
回帰分析を行うことで売り上げや価格などの項目に対して、関係性を見たい項目との関係性を数値で表せます。 また、その関係性がどのくらい強いのかまでを把握できることから、様々な分析でデータの把握に用いられているのです。
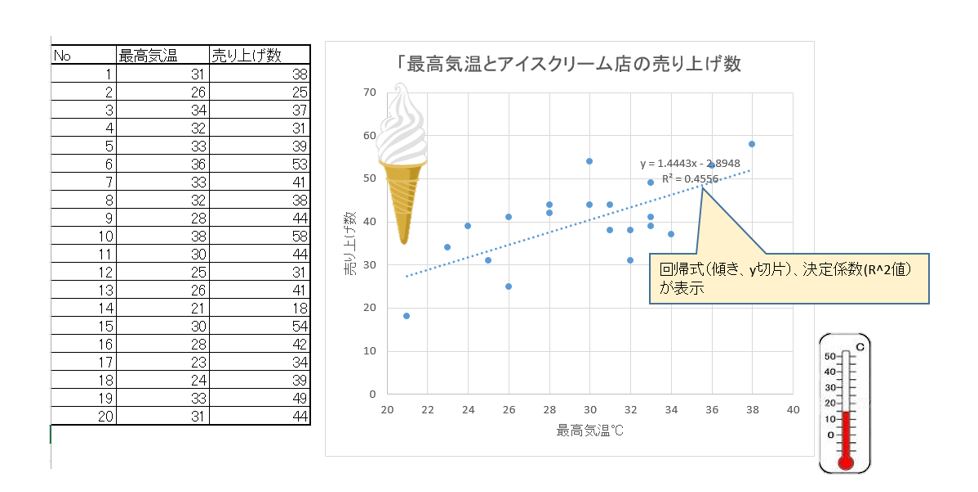
単回帰分析で予測
コンビニ店ののアイスアイスクリームの売り上げ数と最高気温から今日の来店客数から予測する場合。
回帰式から今日の最高温度が分かれば客数が予測できる!
重回帰分析で予測
日本経済の消費関数の予測をする。
被説明変数は消費(c)、説明変数は、所得(y)と利子率(r)である。
エクセル等で偏回帰係数で求め、説明変数が確定したら実際に必要な数値を重回帰式に代入し、目的変数(結果)を算出します。
重回帰式:
目的変数=(偏回帰係数×説明変数1)+(偏回帰係数×説明変数2)+(偏回帰係数×説明変数3)+…+定数項
上記の例の場合は推定された回帰式は, 次のようになる。
消費(円)= 0.402×所得(円)- 3032.417×利子(%)+78203.078
ロジスティック回帰分析で予測
ロジスティック回帰分析は2値に分類する手法です。
ロジスティック回帰分析を行うことで、商品が売れるかどうか、サービスを継続してくれるかどうかなど「はい」か「いいえ」で知りたい情報を予測できます。
例えば不整脈症状が「ある患者」と「ない患者」のグループに喫煙有無、飲酒有無、ギャンブル嗜好についてのアンケートに回答してもらい、喫煙、飲酒、ギャンブルによる不整脈症と関係を調査します。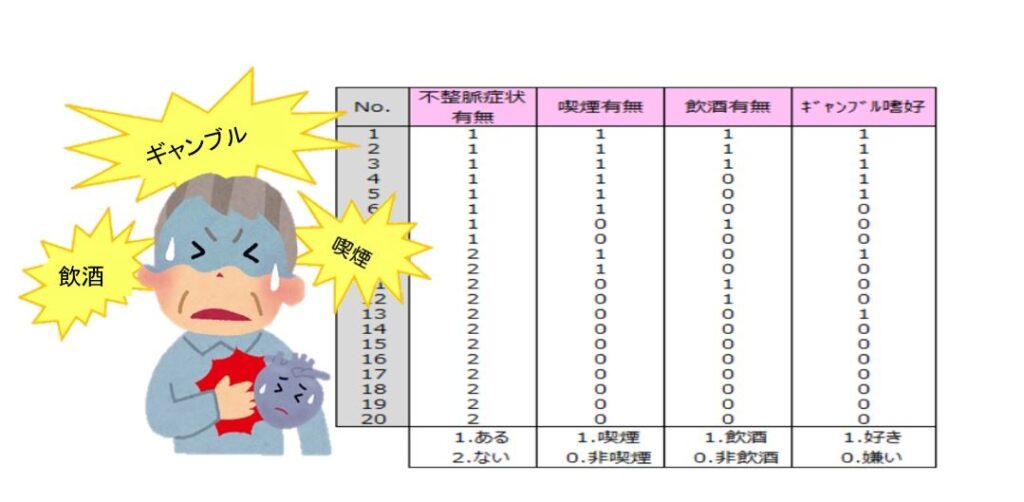
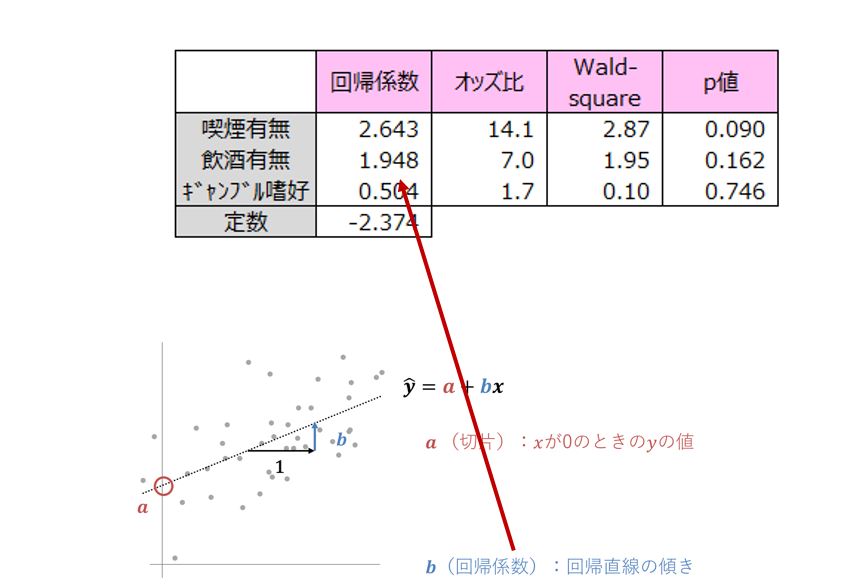
エクセル、SPSS等の統計分析ソフトを使用して回帰係数、オッズ比を算出します。
回帰係数はモデル式の係数です。
オッズ比は説明変数の目的変数への影響度を調べる尺度です。値が大きいほど影響度が高い項目といえます。オッズ比から、不整脈症状の原因要因の1位は喫煙の有無で、次に飲酒の有無となります。ギャンブル嗜好は、不整脈症状にそれほど影響がないことがわかります。
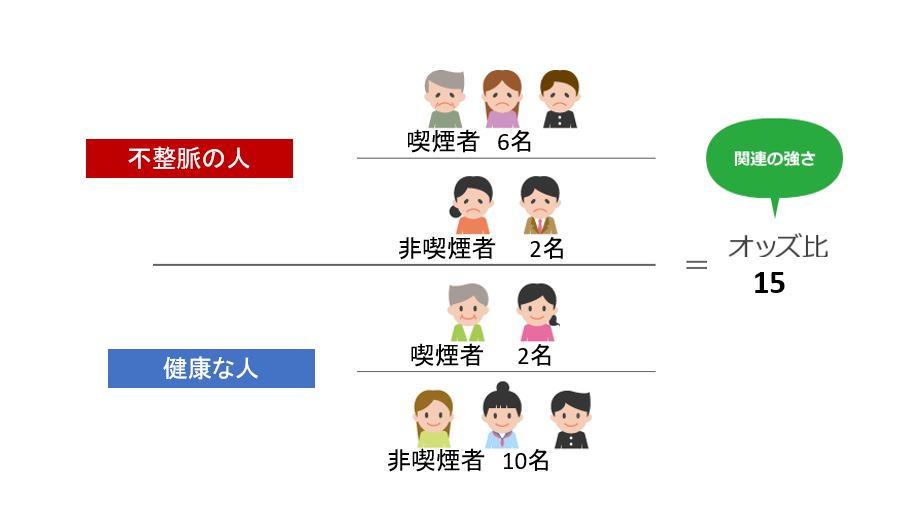
*オッズ比とは
ある因子(環境・食べ物・嗜好品等)がある病気の原因であると仮定したとき、その因子と病気との間に関連があるか無いかを調べます。
オッズ比とは、その関連の強さの指標で、オッズ比が高いほど、その因子と病気の関連性が高いことを示します。
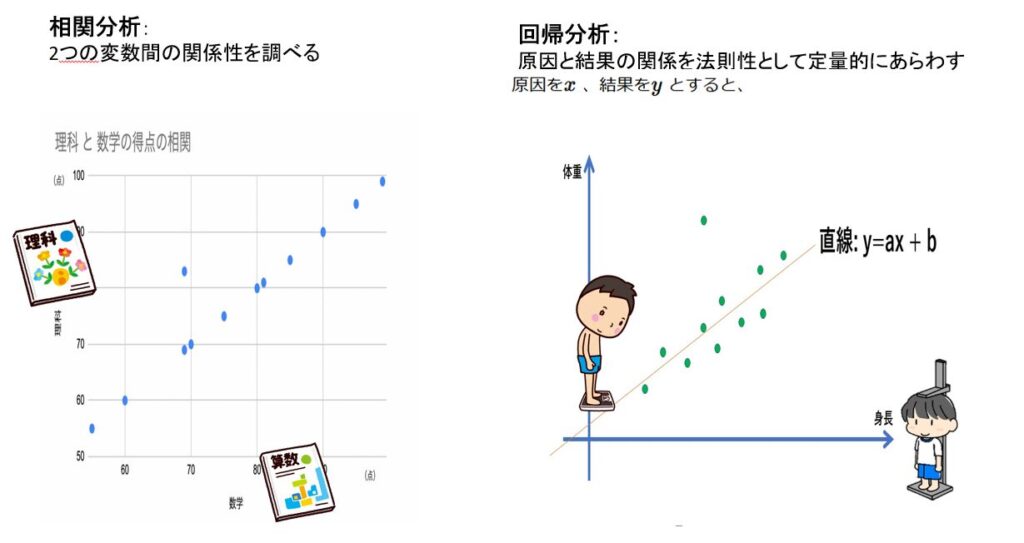
回帰分析と相関分析の違いは
相関分析と回帰分析の違いは、 お互い同じ程度の影響力と考える相関係数か、 データXでデータYを予測すると考える回帰式かの違い。
相関分析は、2つの変数の関係を定量的に表すために使用します。 相関分析では、片方の変数が変化したときに他方がどの程度変化するかを示す相関係数を算出し、2変数間の線形関係を評価します。
一方、回帰分析は結果変数と危険因子または交絡変数との関係を評価する相関分析の関連手法です。