3分で分かる !統計調査、サンプリング、標本調査の概要解説
統計調査は集団の全域にわたる数量的諸性質を観察・分析するために行う調査。調査対象から、全数調査・標本調査(部分調査)・実態調査などに分類される。
総務省統計局が行う国勢調査、事業所・企業統計調査、人口推計、労働力調査、家計調査などを総称して呼ぶ時に用いる場合もある。
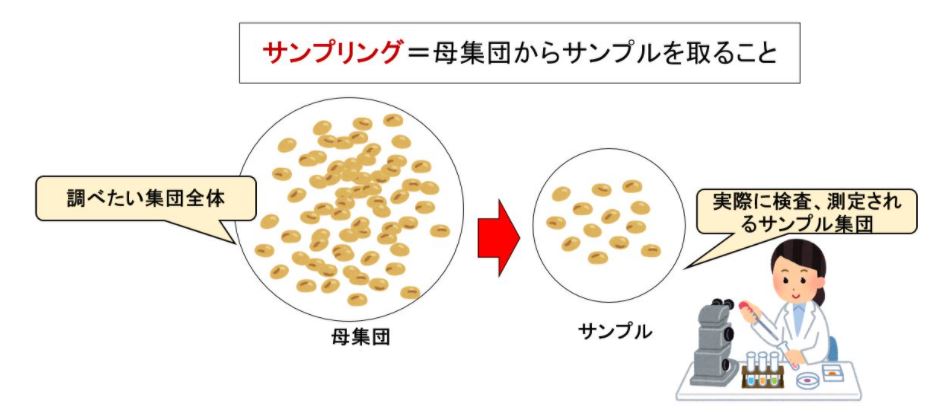
一方、サンプリング、標本調査とは『母集団からサンプルを取ること』抽出、標本抽出、抜取、試料採取ともいう。
標本調査は社会現象をひとつの工程と考えて母集団から一部の標本を採取して調査、観察するサンプリングのひとつである、例えばテレビの視聴率、内閣支持率、面接調査等がある。
中国語では抽样、英語ではsamplingと呼ぶ。
現在の社会では政府、企業を問わず大量のビッグデータを収集して人口、価格等の将来の予測をしています。
しかし、この統計数字を得るために実施する『全数検査』では膨大な時間、費用を要します、”十を調べて十を知る”方式である『全数検査』では迅速に我々が必要と知る統計数字を得ることが困難です。
そこで現在の社会では効率的でコストも掛からない調査対象の一部を抽出して調査を行うと方式『標本調査』という方法が用いられています。
しかし、”一を聞いて十を知る”方式である『標本調査』では恣意的なサンプルの選び方をすれば全体像の情報が反映されてない統計数字になってしまします。
具体的に言うと中国共産党が公表している各種の統計データ等です。
そこで正しくビッグデータを解析する前に『標本調査』つまり、正しいサンプリングの方法を知ることが必要となります。
以下に、「統計検査」「標本調査」「全数調査」の各用語を、英語・中国語・スペイン語でどう呼ぶかを一覧表にまとめました。
| 日本語 | 英語 | 中国語(簡体字) | スペイン語 |
|---|---|---|---|
| 統計調査 | Statistical Survey | 统计调查 (tǒngjì diàochá) | Encuesta estadística |
| 標本調査 | Sample Survey | 抽样调查 (chōuyàng diàochá) | Encuesta por muestreo |
| 全数調査 | Census | 普查 (pǔchá) | Censo |
何故、統計調査、サンプリングするのか?
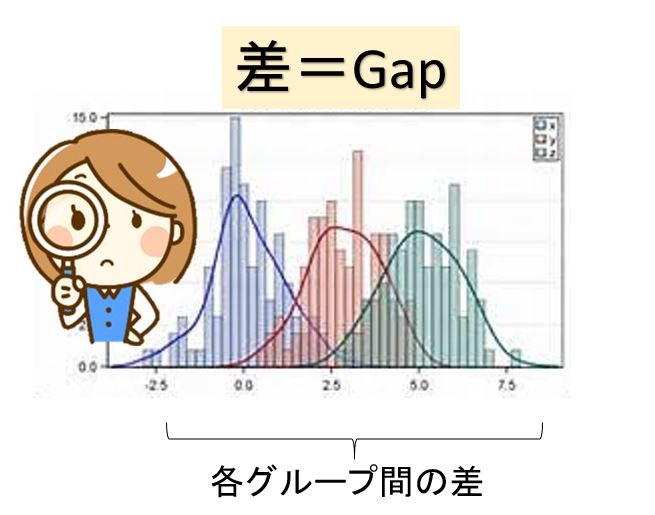
統計調査及びサンプリング、標本調査する目的は社会、会社、工場で発生する問題を解決し、改善する為に幾つかのグループを比較し、その差を検証し、分析し、改善する為です。
ですから,どんなことを比較したいかという目的を整理してデータを集めないと,データはあるが,分析、解析ができないということになります。
たとえば気温のデータならば,温度計のような測定器があり,そのモノサシを使って「測定値」が得られるわけです。同様に統計調査の場合も,どんなモノサシを使って測った数値かを考えて解釈しないと,データの本当の意味はわかりません。あくまでも,何らかの現象を比較したいという目的があり,そのためにサンプリングしてデーターを収集するのです。
また大気汚染について調べたい場合,一酸化炭素と窒素酸化物の排出量でとらえるのが通例です。しかし,この種の計量値だけで,大気汚染のすべてがわかるわけではありません。さらに偏差値というのも,進路指導の際に,うまく学校を選んで入学するのには便利な数値ですが,生徒の全人格的な能力までは測ることはできません。
つまりどんな統計数値も,本当に知りたい現象の,ある側面しかとらえていないことが多いのです。ですから,どういう観点から測っている数値であるかをきちんと認識した上で,一応の判断材料として用いることが大切です。
それを万能視して,数字だけをひとり歩きさせてしまうと,誤解が生じ、色々な問題が発生します。
標本調査と全数調査の違い
「標本調査」と「全数調査」は、データを収集・分析する際の基本的な調査方法であり、それぞれに特徴と使いどころがあります。以下にその違いをわかりやすく表にして説明します。
標本調査 vs 全数調査の比較表
| 項目 | 標本調査(サンプリング調査) | 全数調査(センサス) |
|---|---|---|
| 定義 | 母集団の中から一部を選んで調査 | 母集団すべてを調査する方法 |
| 対象の範囲 | 一部(例:1000人中100人) | 全体(例:1000人すべて) |
| コスト | 低い(部分的な調査のため) | 高い(全件調査のため) |
| 時間 | 短い | 長い |
| 精度 | 推定による誤差がある | 誤差が少ない(誤差=測定誤差のみ) |
| 実施の難易度 | 比較的容易 | 実施が困難な場合もある |
| 活用例 | 市場調査、品質管理、世論調査など | 国勢調査、従業員の健康診断など |
それぞれの活用シーン(具体例)
● 標本調査の例
-
食品工場での抜き取り検査(すべての商品を壊さずに検査する)
-
顧客満足度調査(全員に聞けない場合)
-
新製品の市場調査
● 全数調査の例
-
国勢調査(日本のすべての世帯対象)
-
工場の**初回製品検査(初物チェック)**など品質保証上重要な工程
-
社内の全従業員への研修履歴調査
選び方のポイント
| 判断基準 | 適した調査方法 |
|---|---|
| コストや時間を抑えたい | 標本調査 |
| 高精度・正確さが必要 | 全数調査 |
| 対象数が非常に多い | 標本調査 |
| 対象数が少ない | 全数調査 |
標本調査のメリットとデメリット
標本調査(サンプリング調査)は、全数を調べずに母集団の一部から情報を収集する方法で、特に効率とコストの面で有利ですが、注意すべきデメリットもあります。
標本調査のメリットとデメリット
| 区分 | 内容 |
|---|---|
| メリット | |
| コストが低い | 母集団全体を調べるよりも調査費用を大幅に削減できる。 |
| 時間が短い | 少ない対象を調べるため、短期間で結果が得られる。 |
| 労力が少ない | 人手や物資、機材を最小限に抑えられる。 |
| 非破壊検査が可能 | 破壊検査が必要な製品(例:食品、金属など)でも標本調査なら対応可能。 |
| 分析に集中できる | 少ないデータでも精度の高い統計手法で意味ある結果を導き出せる。 |
| デメリット | |
|---|---|
| 誤差が発生する可能性 | 母集団全体の傾向とズレが出る可能性がある(サンプリング誤差)。 |
| サンプルの偏り | 偏った標本を選ぶと、調査結果が信頼できなくなる(バイアス)。 |
| 小さな差が見えにくい | 標本数が少ないと、わずかな違いを検出しづらい。 |
| 母集団の構成が不明な場合は難しい | 母集団の構造が明確でないと、正しいサンプリングが難しくなる。 |
| 結果に対して説明責任が問われる | 「なぜそのサンプルを選んだのか」が問われることもある。 |
こんなときに向いている
-
対象が多数で、全数調査が現実的でないとき
-
製品の破壊検査やコストを抑えたいとき
-
おおまかな傾向を早く把握したいとき
全数調査のメリットとデメリット
全数調査(センサス)は、母集団のすべての要素を対象に調査を行う方法です。高精度な情報が得られる一方で、実施には多大なリソースが必要です。以下にメリットとデメリットを整理してご紹介します。
| 区分 | 内容 |
|---|---|
| メリット | |
| 精度が非常に高い | 全員を調べるため、統計的な推定誤差がない(=誤差は測定誤差のみ)。 |
| 母集団全体の正確な実態把握が可能 | 例えば国勢調査では全国の人口・世帯の分布を正確に把握できる。 |
| 分析の自由度が高い | サブグループ(年齢別・地域別など)ごとの分析も可能。 |
| 政策・経営判断の信頼性が上がる | 重要な意思決定の根拠として説得力があるデータが得られる。 |
| 再利用可能な基礎データになる | 一度の調査で多用途に利用できる(人口統計・市場分析など)。 |
全数調査が向いているケース
-
対象数が少なく、全員調査しても現実的なコストと時間で済む場合
-
政策や法制度などにかかわる社会的に重要な調査
-
高い正確性が求められる品質保証やトレーサビリティ管理
製造業での例
| 調査内容 | 実施方法 |
|---|---|
| 初物(初回製品)の検査 | 全数検査(量産前の全品確認) |
| ロット不良時の再検査 | 問題ロットの全品再チェック |
| 出荷前の重大部品検査 | セーフティクリティカルな部品などに全数調査を実施 |
世論調査と全数調査
「世論調査」と「全数調査」は、調査対象の範囲と目的が異なる調査手法です。混同されやすいですが、本質的に違うものです。以下に、わかりやすく整理してご説明します。
世論調査と全数調査の違い【比較表】
| 項目 | 世論調査(よろんちょうさ) | 全数調査(センサス) |
|---|---|---|
| 目的 | 国民や有権者の意見・傾向を知る | 正確な実数を把握する(例:人口、売上等) |
| 調査対象 | 母集団の中から選ばれた一部(標本) | 母集団のすべて |
| 代表的な方法 | サンプル調査(ランダム抽出・電話・ネット等) | センサス(全員調査、記入式・電子式など) |
| 費用と時間 | 少ない | 非常に多くかかる |
| 精度 | 推定値(誤差を含む) | 実測値(推定不要) |
| 例 | 内閣支持率調査、選挙前の世論調査 | 国勢調査、従業員の全員健診、全品検査 |
それぞれの特徴と補足
世論調査とは(Sample Survey)
-
有権者や国民の「意見」や「傾向」を知るための調査
-
全員に聞くのは不可能なので、統計的に有効な「標本(サンプル)」を抽出して行う
-
結果は「推定値」で、±◯%の誤差範囲がある(例:支持率54% ±3%)
🔹 使用例:
-
選挙前の支持政党調査
-
社会課題に対する意識調査(例:少子化対策への賛否)
全数調査とは(Census)
-
国民や企業など、対象となるすべてを調査する手法
-
結果は「推定」ではなく「実数」になる(誤差なし)
🔹 使用例:
-
国勢調査(日本では5年ごとに実施)
-
全国事業所調査(全企業・事業所が対象)
一言で言うと…
| 調査名 | 調査の性質 |
|---|---|
| 世論調査 | 一部を調べて全体を推定する調査 |
| 全数調査 | 全体を調べて全体を把握する調査 |
統計調査の進め方
対象集団の大きさや特性を数量的に把握するための統計調査は,周到な計画・準備にもとづいて実施されなければなりません。調査目的に応じて,対象集団の全体について調べる全数調査の場合もあれば,全体から一部分を無作為抽出する標本調査の場合もあります。
統計調査の計画は,調査目的の明確化から始まり,調査対象集団(母集団)の設定,調査項目の選定や質問文の作成と続きます。
統計調査の規模は,主に予算・人力・日程などから決定されます。調査目的の明確化には,結果の精度の見積りなども含まれます。
引き続いて,調査方法や実査方式が決定されます。
統計調査の準備には,母集団リスト(フレーム)の作成,調査票の作成などがあります。回答の分類基準は他の調査研究との比較を可能にするために,既存の分類基準に準じたほうが賢明です。特に標本調査の場合には,標本の抽出が必要となります。調査票作成の段階で,予備的に調査することをプリテストといいます。
また小規模調査をして調査全体について検討することを,パイロット調査といいます。調査票は,プリテストを通して修正されます。
統計調査の実施には,実査と審査があります。審査はエディティングともよばれ,回収された調査票の空欄や矛盾回答などについて点検することをいい,必要ならば再調査をしなければなりません。結果の処理は,コーディング・ 集計・解析・報告書の作成,の順に行います。
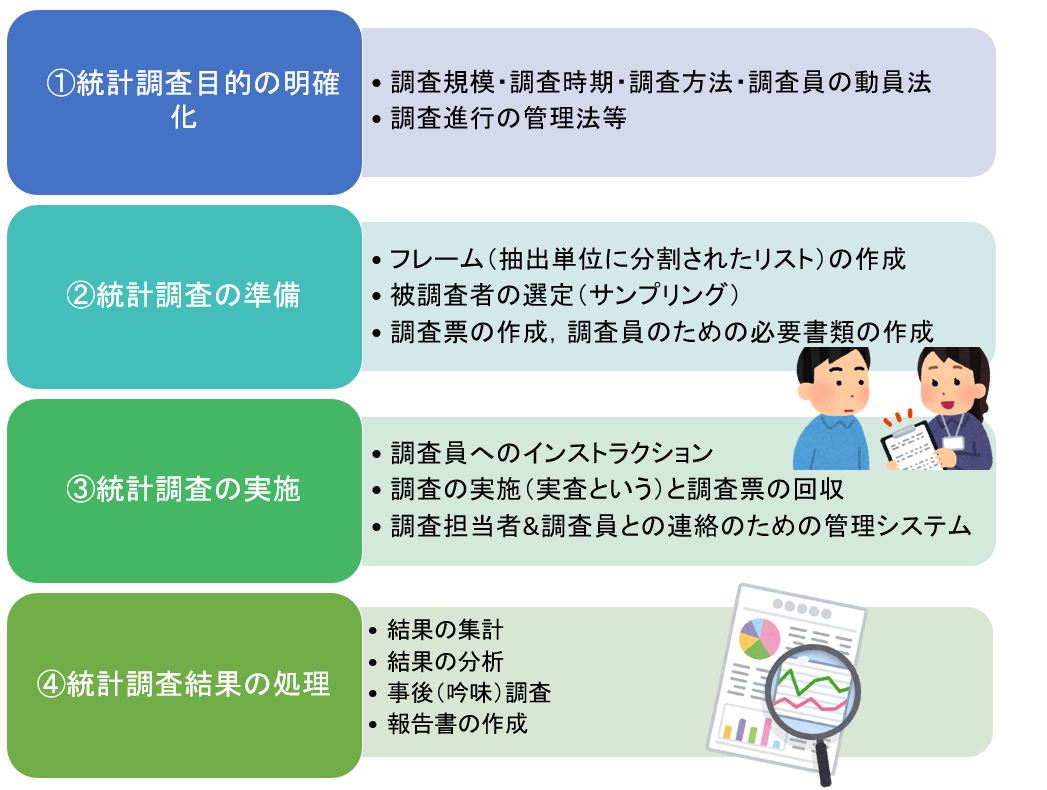
統計調査のステップ
①統計調査の企画(必要なら事前調査も)
統計調査目的の明確化
調査規模・調査時期・調査方法・調査員の動員法
調査進行の管理法等
②統計調査の準備
フレーム(抽出単位に分割されたリスト)の作成
被調査者の選定(サンプリング)
調査票の作成,調査員のための必要書類の作成
③統計調査の実施
調査員へのインストラクション
調査の実施(実査という)と調査票の回収
調査担当者ど調査員との連絡のための管理システム
④統計調査結果の処理
結果の集計
コーディング・単純集計・クロス集計
(性別・年齢別・職業別・地域別等とのクロス)
結果の分析
統計調査結果の妥当性についでの検討
調査不能集団のフェイスシートによる偏りの検討
事後(吟味)調査
報告書の作成
結果の核心部分を要領よくまとめ,一般利用者にもわかるよう整理する
統計調査票、アンケート表
信頼性,有効性の高い情報は,良い調査票から得られます。質問に入る前には,調査目的や結果の使途などを簡明に記し,回答方法なども記載する必要があります。個人の基本的属性(性別,年齢,学歴,職業など)に関する質問は,フェイスシートとよばれています。これらは,被調査者に抵抗感を与えることがありますから,必要最小限にして質問の末尾につけるのが通例です。
質問数はできるだけ少なく,筒単明瞭な表現を旨とすべきです。特に専門用語は避け,具体的な事実を尋ねる形がベターです。
1つの質問で2つ以上の事柄を含めないようにし,否定形の質問も避けたほうが賢明です。回答者に 質問の意味をはっきり理解させることが肝心です。
回答者は,彼自身が理解した内容でしか答えてくれません、 回答の形式には,2項選択,多項選択,複数回答などの他に,あらかじめ選択肢を設けない自由回答法などがあります。
複数回答の場合には,いくつまで回答するかを明示します。自由回答方式は,空欄が多くなりやすく,集計に際しても分類・コード化する必要があります。
しかし,回答が制限された質問では得られない情報も期待できますから,質問の内容に応じて適宜採用します。
質問の順序は,単純なものから順次核心的な質問へと配列します。関連のある質問は,できるだけまとめて並べます。質問の回答結果によって,次に進む質問の位置が異なる場合には,そのことを指示することも必要となります。
統計調査票、アンケート表のテンプレート(エクセル版)のダウンロードのサンプルは下記。
統計調査前の事前調査(プリテスト)
通常の統計調査では,すでに同種の調査を実施したことがあるとか,類似調査の報告書が手に入る場合には,事前調査は行わずに,すぐに本調査を行うことになります。
そうでない場合には,より適切な調査結果を得るためにも,事前調査を行うほうが賢明です。事前調査を行う主な目的として,次のような点が考えられます。
①調査を実際に行ってみることによって,その調査固有の問題点を明らかにすることができる。
②とりあげる調査項目が,調査の目的と照らしてみて必要十分かどうかを確かめてみることができる。特に各質問は,回答パターンの“違いをみる”ことにある。皆が同じ答というのでは,質問した意味がない。事前調査により,無意味な質問を修正・削除できる。
③質問の言葉使いなどが適切かどうか確かめられる。
④質問に対する回答選択肢の適正さが検討できる。
⑤自由回答形式で質問してみて,制限回答形式の質問に作りかえることができるかどうかが検討できる。
⑥調査の核心的な質問に対する回答結果の平均などを眺めてみて,必要な標本数を見積ることができる。
⑦本調査の精度を上げるための,層別抽出の方法に関する補助情報を得ることが期待できる。
なお事前調査を行うときの標本数は, 100~200程度が通例です。もちろん,無作為抽出された標本を用いて行わなければなりません。
母集団と標本(サンプル)
標本調査では,母集団と標本(サンプル)がキーワードです。
何らかの結論を得ようとしている集団は,調査対象集団とよばれています。この集団は必ずしも人間だけとは限らず,ある家庭電気製品であるとか,全国の小売書店のように,何か知りたいと思うものの集まりが,全て調査対象集団となりえます。
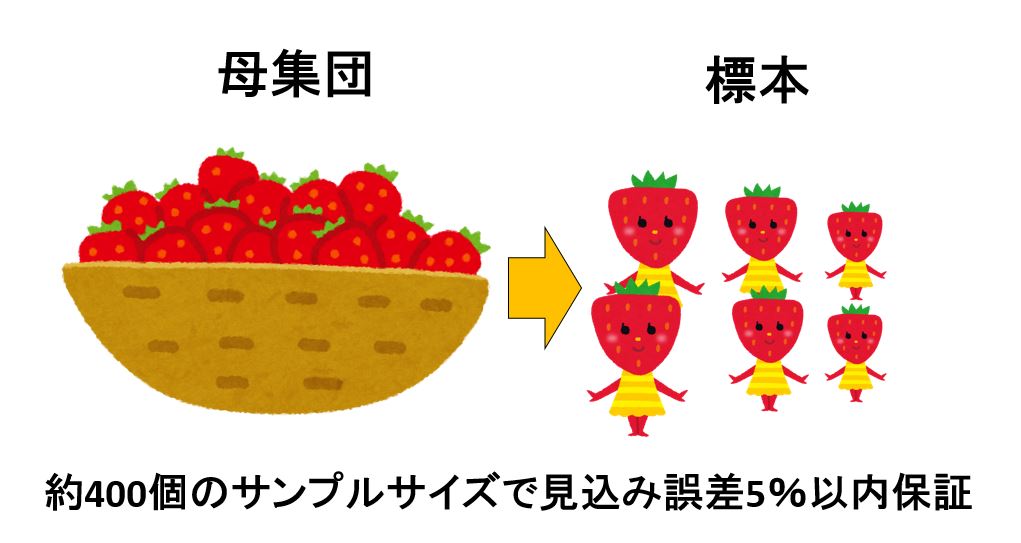
この調査対象集団から,ある一定のやり方で一部分を抽出すると決めたときに,その集まりを母集団と名づけます。
さらに,調査用に抽出された一部分は,標本(サンプル)とよばれています。全体を調べずに,「全体の ソックリさんを選びだし 特性調べる 「標本調査」を行えば,調査のための費用や時間が大幅に節約できます。
標本調査に対して,全体を全て調査する場合を悉皆調査(全数調査)といいます。特に,人口調査、国勢調査に関する全数調査は,センサスとよばれています。
よい標本とは,全体とよく似ている一部分のことです、乱数表を使用し、無作為にサンプルを抽出します、無作為標本調査と呼びます。
統計調査リストの作成と標本抽出
標本の抽出作業を進めるには,調査対象集団である母集団についての,リスト(たとえば選挙人名簿や住民票など)が必要になります。
むしろ,利用できるリストのほうから逆に,母集団が定義されることも多いのです。また,
利用できるリストがないときには,調査に先だってリスト作り(リスティングという)が必要になります。ただ全対象のリスティングは不可能ですから,抽出操作の基本となる適当な大きさの抽出単位を考え,調査対象の部分についてだけリスティングを行うのが通例です。抽出単位に分割されたリストのことをフレームとよんでいます。
全国調査の場合,全ての市区町村を調査することはありません。まず,各市区町村の人口規模に比例させた層別抽出で,調査対象の市区町村(第1次抽出単位)を選定します。
次に抽出された市区町村の中から,調査区や投票区のような調査対象地区(第2次抽出単位)をやはり市区町村の人口に比例した個数だけ選出します。
最後に,指定された調査対象地区から,単純無作為抽出法(実際には系統抽出)により調査対象の個人を選ぶことになります。
たとえば,国勢調査を行うために「調査区」というのが定められていて,これは1人の調査貝の担当部分に相当し,50世帯前後のリストが含まれています。調査対象の市区町村で閲覧できる「調査区一覧表」には,調査区ごとの人口概数が出てますから,その人口数に比例した抽出確率で調査用の調査区を選ぶことができます。
統計調査の実施
調査の計画や調査票がいかに完全であっても,調査自体が正しく実施されなければ,正しいデータは集められません。標本として抽出された調査対象者を訪問・面接し必要な情報を得る一連の作業のことを,実査といいます。
特に全国規模の調査の場合には,調査を企画する人の目の届かないところで,大勢の調査員が被調査者と質問・回答を行うわけですから,雑多な混乱要因が内包されています。
調査企画者は,調査実施の全行程を上手に管理運営できるよう,周到な配慮が必要となります。
調査にあたる調査員を選任する際には,次のような条件を考慮することが大切です。まず,服装や言葉づかいなど相手に特異な感じを与えかねない人物は避けたほうが賢明です。
また,理解力・判断力が平均以上であること。これは,調査の主旨や質問の意味を正しく理解し,回答者から適正な情報を得るためにも不可欠です。
さらに健康で,忍耐力のあるタイプが望ましい。回答者のなかには,応対の冷酷な人や回答を拒否したがるタイプも少なくありません。忍耐強く調査に協力を求め,不在がちな回答者には再三訪問をくり返すような調査員が望ましいのです。
調査の完了した調査票を受けとることを回収といいます。個々の調査票についての記入もれや誤記入の有無を確かめ,調査員の記憶で処理できるものはその場で処理しなければなりません。また,必要と判断されたら,調査員に再調査を命じることもあります。
統計調査結果の集計・解釈・報告
回収された記入済み調査票の情報を必要な統計表にまとめる作業を,集計といいます。最近では,集計作業の大部分がインターネットを通してコンピュータで処理されるようになりました。
コンピュータ処理を行うには,まず調査票の記入事項をコード化する必要があります。この部分は人力に頼らざるを得えませんから,入力ミスなどの誤差要因が入りこむ危険性があり,念入りなチェックを行うことが大切です。
まず,各調査項目ごとに,どの答えがどのくらいあったかを整理する単純集計を行います。次いで,2つ(以上)の項目を同時に集計するクロス集計を行い,調査項目間の関連性などを調べます。
得られた統計数字の見方を説明し,利用上の限界などを注記することを解釈といいます。調査結果の解釈には調査の全容を把握すると共に,母集団は何か,さらに得られた数値の精度がどの程度かを見積る必要があります。
調査結果が利用者の目に触れるのは,主として報告書を通じてです。したがって報告書の作成では,利用者がよく理解できる表現で,納得のいく解釈を加えて提供することが大切です。
なお利用の限界についても,付記することを忘れてはなりません。さらに結果の全容を端的に説明するには,グラフ表現を多用するほうが効果的です。
さらに,報告書はできるだけ迅速に発表することが大切です。貴重な情報であればそれだけ,時期遅れとなる情報の劣化を防ぐ必要があるからです。
サンプリング、標本調査
サンプリング、標本調査、標本抽出の思考
サンプリング、標本調査、標本抽出の思考、考え方は人類の歴史はじまって以来のものと思われます。人類に限らず他の動物も,食物の一部をサンプリングして味見しますがこれは本能によるものです。
人間の場合、自分の食べものと他人のものとを交換しようとしますと,交換対象の食べものを味見することになります。その場合,食べもののごく一部分だけが味見され,残りは試食に用いたのと同じものとみなしていたはずです。
今日でも,電球などの寿命試験の実験では,その電球が切れるまでつけて耐用時間を測定します。しかし,全部の電球で試してしまいますと,家庭で使われるものが一つも残らなくなってしまいます。
全数破壊を避けるためにはどうしても標本抽出を行うことが必要です。
人間には,自分自身をわかりやすいカテゴリーに分類しようとする性癖があります。違ったカテゴリーでの反応パターンには変化があるので,一個人の反応だけで全体の反応を代表させるのは無理です。
しかし,各個人が属するカテゴリーの反応を代表することはできますから,各カテゴリーから抽出された個人が集まれば,全体での主要な反応を代表することになります。さらに各標本が,そのカテゴリーの要素の数に比例して抽出されていれば,母集団全体に占めるカテゴリーのウェイトに比例した代表性をもつことになり,結局,標本全体が母集団全体の反応を忠実に代表することになります。
サンプリングの推定値 精度
一般に,無作為抽出による標本から算出される標本平均や標本比率は,毋平均や母比率にピタリ一致するとは期待できませんが,次のような「統計的法則」を適用できることが知られています。
”母平均の分布が正規分布に従うならば標本分布の分布も正規曲線になる、また母集団の分布が正規分布でなくても標本平均、標本比率の分布が正規分布と近似する!
そこで,正規分布曲線の性質を用いれば,標本平均や標本比率の標準誤差が算出できます。すなわち
標本平均の標準誤差=
$$\sigma/\sqrt{n}$$
標本比率の標準誤差=
$$\sqrt{p\times q/n}$$
ここでnは標本数,σは毋集団の標準偏差,さらにpはある特定の性質をもつ個体の毋比率,q(=1-p)はその性質をもたない個体の比率を表すものとします。
さて,推定値の「精度」は,推定幅と的中率の2つの要因によって規定されます。推定幅が狭く,しかも的中率が高い場合に,精度が高いと表現します。推定幅のことを信頼限界,また的中率を信頼度とよんでいます。
正規分布曲線の性質から標準誤差の2倍を推定幅にとれば,信頼度(的中率)は95%になることがわかります。さらに標準誤差の3倍を推定値幅にとれば,信頼度は100%近くになります。
サンプル数とサンプルサイズ
「サンプル数」と「サンプルサイズ」という言葉の意味について、簡単に解説します。とても良く似た響きですが、まったく違う意味を持っています。
・サンプル数(the number of samples)=標本数・群数
・サンプルサイズ(samplesize)=データの個数・標本の大きさ(通常「n」で表します)
つまり、サンプル数は「何回標本の抽出をおこなったのか」、サンプルサイズは「1回の標本抽出において、いくつの個体を調べたのか」ということになります。
<事例1>
工場の特定のポイントの気温を、4日間にわたり調査、各日で測定した箇所の数が異なるとします。
・1日目:100ヵ所の気温を測定
・2日目:300ヵ所の気温を測定
・3日目:100ヵ所の気温を測定
・4日目:150ヵ所の気温を測定
その際の、サンプル数とサンプルサイズは、
・サンプル数:4
・サンプルサイズ:100、300、100、150
となります。
<事例2>
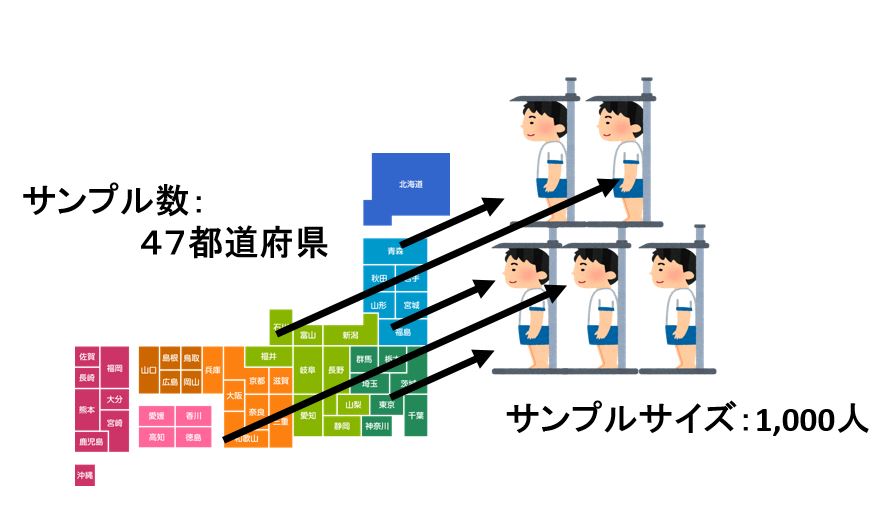
47 都道府県の男子高校生の身長の平均を比較するという調査、各都道府県から無作為に 1000 人を選んで平均を算出したとき,この調査におけるサンプル数,サンプルサイズは
- サンプル数(群数):47
- サンプルサイズ(各群のサイズ):1000 人 / 群
となります.標本抽出を 47 回行ったためサンプル数は 47,各標本の個体数が 1000 人のためサンプル数は 1000 となります.「サンプル数=群数」,「サンプルサイズ=各群のサイズ」です。
サンプリング数、サンプルサイズの決め方
サンプリング数(標本数)が多くなればサンプルから算出される推定値(標本平均や標本比率)が母集団の代表値(一母平均や母比率)に近い値になります。
ところでサンプル数のサンプルサイズを多くとれば,それだけ調査費用、時間も多くかかります。
実用上からみて定まる精度内の推定値が求められればよいのに,それ以上の正確性を追及するのは無駄になります。かといって,あまりにも少なすぎる標本では,これまた使いものになりません。
適正な標本数は,母集団の性質と回答を求める問題の性質によって決まるものです。
たとえば,ある会社の従業員の平均年収を, 10 (万円)の推定幅で95%の信頼度で推定する場合について考えてみます。
以前の調査事例から,標準偏差が約150(万円)です。必要な標本数をnとして
$$2×150/\sqrt{n}=10$$
という関係をnについて解きますと
$$n=(2×150/10)^{2}=900$$
という結果が得られます。これより, 900のサンプルを抽出すればよいことがわかります。
サンプルサイズの求め方 計算式
母比率の95%信頼区間は次の式であり、この式からサンプルサイズを求める。
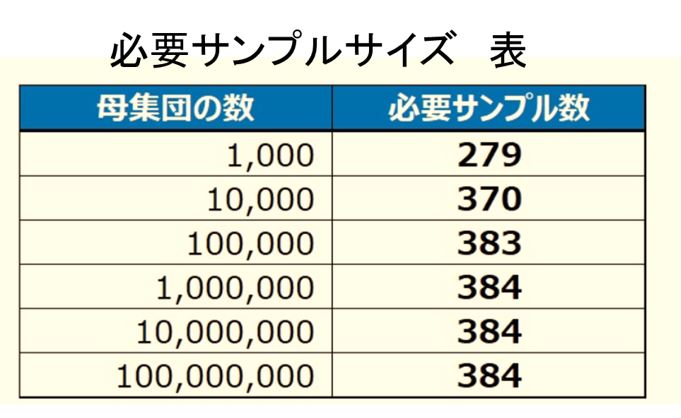
又、許容誤差±5%が場合の必要なサンプルサイズは下記の表からも求めることができます。
そして、10,000を超えると必要なサンプルサイズはあまり変化せず、400以下です。
よって、母集団が1,000以上の場合は、400程度のサンプルサイズを見込めば誤差±5%の範囲内でデータを得る事が可能です。
統計的サンプリングとは?
工程の管理,抜取検査などでは,母集団からサンプルを抜き取り,そのサンプルの情報から母集団の工程平均,品質などを推定している。
その場合,問題になるのは
①母集団がはっきりしているか?
②サンプルが真の母集団を代表しているか?
③サンプルの抜き取り方が正しいか?である。
もし,そのサンプルが,真に母集団を代表するサンプルでないとしたら,得られた情報は間違ったものとなり,判断も正しくないものとなる。
これらの誤りをなくするため,正しいサンプルの抜き取り方など,すなわち,サンプリングの進め方について学習することが必要となる。
一般によいサンプリングとは,費用が安くて,精度がよく,かたよりがなく,結論が早く出て,信頼でき,目的にあった情報を得ることができることである。
“サンプリング”とは母集団からサンプルを取ること。
[JIS Z 8101-2 (統計一用語と記号一第2部:統計的品質管理用語)]である。
サンプリングは得られたサンプルを測定し,データから母集団について目的にあった必要な情報をつかむために行うものである。そのため,サンプリングを検討する場合には,まず母集団を明確にしておかなければならない。
“母集団”とは考察の対象となる特性をもつすべてのものの集団.”(JIS Z8101-2)である。
サンプリングの目的は母集団のある状態,たとえば,母平均,母不良率などを知るためであるので,サンプリングにおいて大切なことはわれわれの知りたい内容(目的)と母集団”を一致させておくことである。
母集団には,無限個と考えられる母集団の無限母集団と,有限個と考えられる母集団の有限母集団がある。
一般に工程の状態を推定する場合は無限個の品物を製造するものと考えて,無限母集団を想定する。
抜取検査でロットの品質を推定する場合は,有限個の品物の集団を対象としているので,ロットは有限母集団となる、これら母集団とサンプルの関係は下図に示すとおりである。
関連記事:抜き取り検査と基準 | JIS9015
サンプリングの種類
サンプリング法を大きく分類すると,ランダムサンプリングと有意サンプリングに分けられる。
“ランダムサンプリング”とは,“母集団を構成している単位体・単位量などがいずれも同じような確率でサンプル中に入るようにサンプリングすることと定義されている。
すなわち,母集団のすべての単位体・単位量などが,サンプルに選出される確率を等しくもつようなサンプリングであるといえる。
通常は,ランダムサンプリングを意図しているのであるが,乱数表・乱数サイ(正二十面体サイコロ:日本規格協会)を使用する。
これは,どの品物が特に抜き取られやすい,あるいは抜き取られにくいというようなことのないクセのない抜き取り方である。
一方,有意サンプリングとは,“確率が同じとはいえないようなサンプリング”と定義されている、有意サンプリングには,やむを得ず有意サンプリングとなる場合と,意図的に有意サンプリングにしている場合がある。
又、乱数表・乱数サイをしないで適当にサンプリングする場合、アメリカのデミング博士はチャンク(chunk)と呼んでランダムサンプリングと区別している、工場などのサンプリングでは,この方法がよく使われている。
有意サンプリングの例としては,プレス加工時の初物検査がある、この場合は,技術的情報などからランダムにサンプリングせず,意図的に初物数個を検査するものである。
このサンプリング法は,母集団の性質がよくわかっており,学問的な理論や経験的な知識から,代表とみられるサンプルが得られる場合には,良い結果を得ることができる。
しかし,サンプリング誤差を客観的に評価することが不可能であり,また,方法を誤ると調査する人の主観が入りやすくなり,サンプルの大きさを多くしても,代表性を高めることにならないという欠点をもっている。
したがって,有意サンプリングの実施にあたっては,これらの点について十分に吟味することが必要である。
*乱数サイコロ:乱数を発生するのに用いる0~9までの数値がランダムに得られるさいころ。これは石田保士氏の考案による正20面体の各面に0~9までの数値が2回ずつ配置されている。
ランダムサンプリングの種類
サンプリング単位
JIS Z 8101-2によれば,“サンプリング単位”とは
ランダムサンプルの手順
ランダムサンプリングは,一般に次の手順のように実施される。
手順1
目的に応じて目標精度を決める。
何を知るためにサンプリングを行うのか目的を明確にする。
たとえば,今日生産された製品の平均引張強さを知りたい,あるいは東京都在住の5歳の子供の平均身長が知りたいなどである。
次に,どの程度の精度で知りたいのか,目標精度を決める、その際に精度の妥当性について十分に検討することである。
例として±5cmの精度で知りたい,あるいは標準偏差2cmの 精度で知りたいなどを検討することが必要である。目標精度がはっきりしていないと,何個のサンプルをとってきたら良いのかが明確にならない。
手順2
採用するランダムサンプリングの種類を決める。
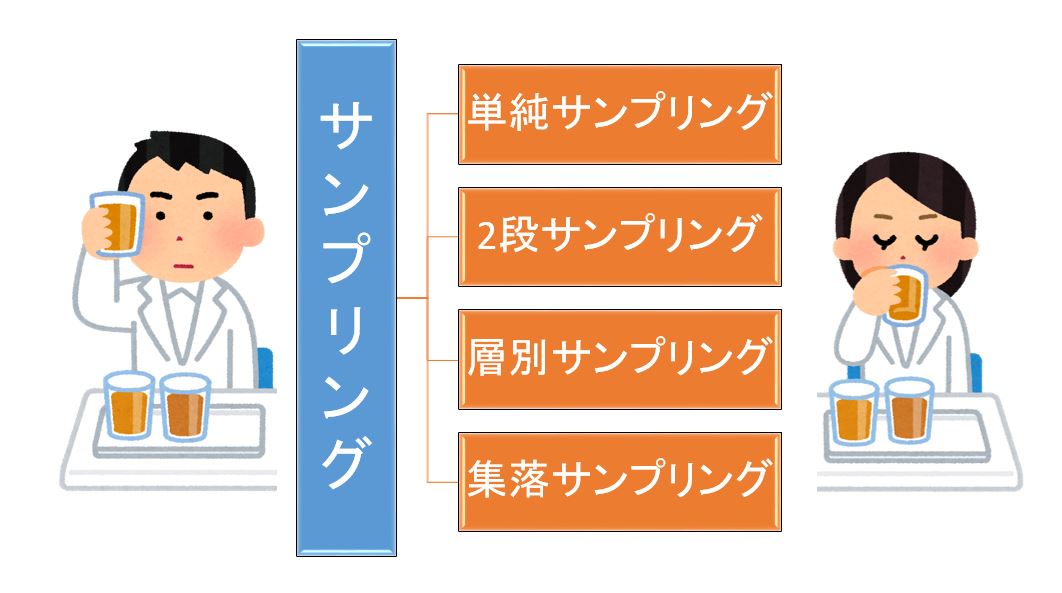
ランダムサンプリングの種類の決定とは単純サンプリング,2段サンプリング,層別サンプリング,集落サンプリングのいずれを採用するかを決めるごとである。
精度の立場からは,できるかぎり層別サンプリングを採用することが好ましい。
手順3
必要な母集団の分散を推定する。
採用するランダムサンプリングの種類によって必要とする分散が異なる。
たとえば2段サンプリングであれば,副ロット間(1次サンプリング単位間)のばらつきと,副ロット内(1次サンプリング単位内)のばらつきの大きさを推定する。
どのサンプリングを採用したらどんな分散を推定しなければならないかは各種サンプリングの“分散の期待値”を参照する。
手順4
サンプルの大きさを決める
“分散の期待値”の公式より,サンプルの大きさを計算する。
手順5
計算された必要な大きさのサンプルをランダムにサンプリングする決められた大きさのサンプルを乱数表あるいは乱数サイなどを用いて,サンプリングする。
手順6
サンプルを測定してデータを得る。
たとえば,サンプルの引張強さなどを測定して,データを得る。
手順7
実現精度と目標精度を比較し,検討する。
たとえば,実現精度が目標精度に未達であれば,サンプルを追加するなどを検討する。
“サンプリング法の設計”とは目標精度が達成でき,かつ作業性,経済性などが満足できるサンプリングのやり方を設計することである。たとえば,どのランダムサンプリングを使用したらよいか,何個のサンプルをとったらよいのか,などを設計することであるので,手順の1から4までを実行することである。
なお,本サイトでは平均値の推定”の場合のサンプリング法について記載していますので分散の推定,計数値の推定については他の書籍を参考にしてください。
単純サンプリングの具体な手順
単純サンプリングとは,母集団を層あるいは部分に分けることなく,そのまま母集団から乱数表あるいは乱数サイを用いて,ランダムにサンプリングすることである。
たとえば,1000個の品物の中から,10個の品物を単純サンプリングするには,1000個の品物に番号を付け(具体的にマジックインキで番号を書き込むというのではなく,積荷を左下側の左隅をNo. 1として順に右へ,上へと数えること,あるいは品物を移動させ,移動させた順にNO1, No. 2と数えることなどであり,実際に品物に番号を打たなくても,その番号がわかるようになっていればよい.)
乱数表・乱数サイから,1~1 000 個の範囲の乱数列を作り,重複を除いて10個の乱数を選び,選んだ乱数に相当する番号の品物を抜き取る。
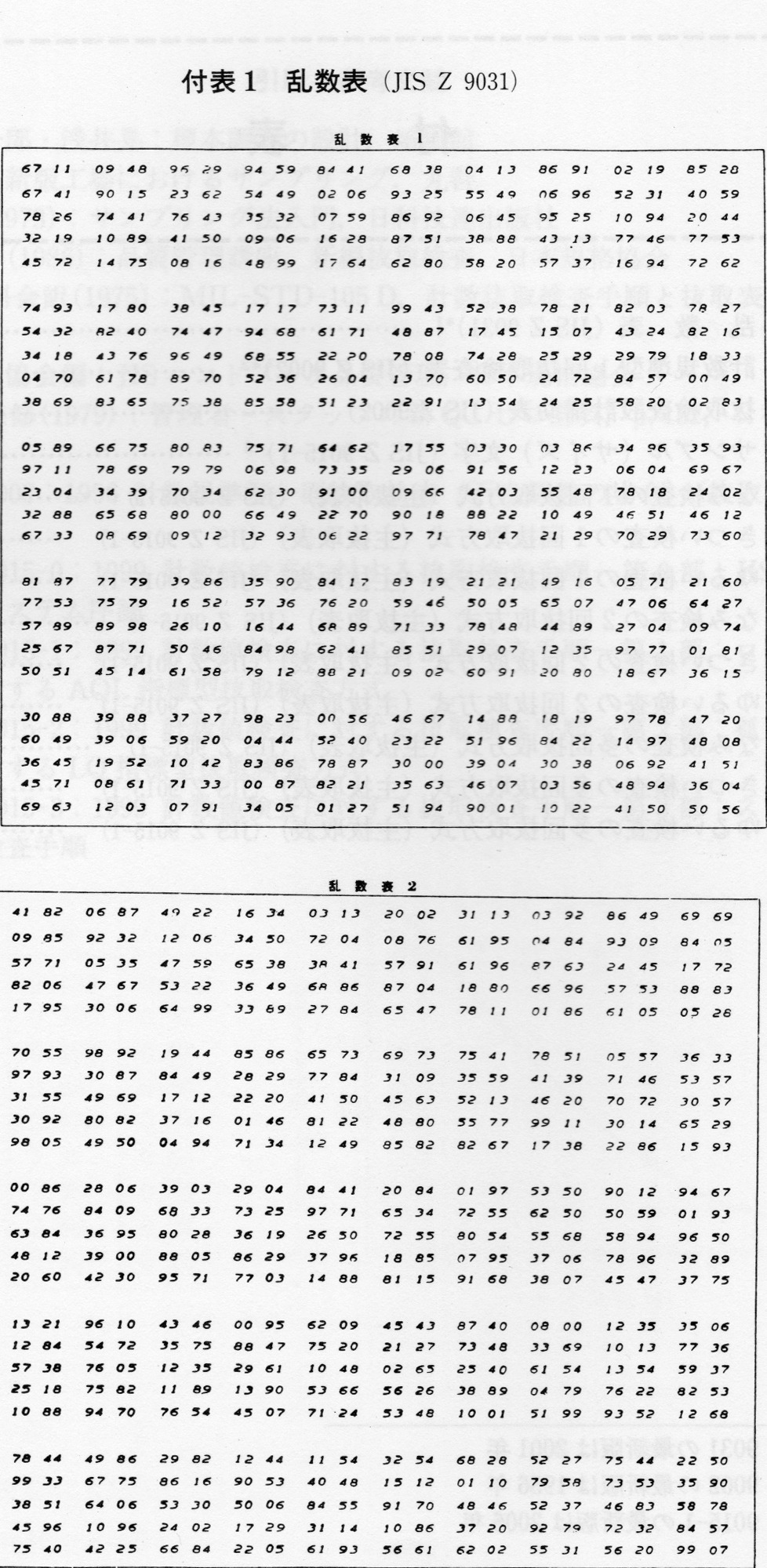
乱数表
乱数表とは
乱数表には,矩形乱数表,正規乱数表など種々の乱数表があるが,ここではサンプルを指定するのに用いる矩形乱数表について述べる。
矩形乱数表は 0・ 1・ 2・ …・8・9の数字が次の特徴をもって配置されている。
① どの数字でも同じくらいの出現率をもっている。
② ある数字の後にある数字が特に出やすい,あるいは,特に出にくいというようなことはない。
③ 相続く2けた以上の数字が特に出やすい,あるいは,特に出にくいというようなことはない。
JIS Z 9031 (ランダム抜取方法)では,40,000個の数字が,1, 000 個ずつ40
組に分けられて収録されている。本サイトでは,そのうち2組について掲載。
乱数表の使い方(JIS Z 9031)
乱数表は,どこから出発しても乱数であるが,常時,同じ所から出発した数字を使っていたのでは予測可能となるのでランダムではなくなる.そこで,まず,どこから出発するか出発点を任意に決める必要がある。
(a)出発点を任意に決める
乱数表の任意のページの上に,目をつぶって鉛筆を立てて落とし,当たった点に一番近い数字を起点として,連続3個の数字を読み,これを行の番号とする。(この場合,000は1000とみなす)、次にもう一度鉛筆を落として,当たった点に一番近い数字によって列の番号を決める。
(4個ずつの組が1行に10組入っているので,これを左から1~9番および0番として,選ばれた番号の列の左端を出発点とする)
(b)原乱数列を読み取る
1けたの原乱数列または2けたの原乱数列が必要な場合には右へ進む.右端に達したら次の行の左端に移る。
3けた以上の原乱数列が必要な場合は下に進む.下端に達したら,同じページの中で次の列に移る。3けたの場合には,1組4個の数字のうち最後の1個を捨てる。
ページの右下に達したら,次のページの左上に移る.最後のページの場合には,最初のページに移る。つまり,出発点をランダムに決めたあとは乱数表の数字を連続して用いる。
【例題1.1】
100個の品物の中から√3個ランダムにサンプリングしたい。何番目の品物を抜き取ったらよいか。
[解答]
任意のページに目をつぶって鉛筆を立てたら,010という乱数を得たので,これを行番号とする.次に同様に鉛筆を立てたら,3という乱数が得たので,これを列番号とする.。JIS Z 9031の乱数表によれば,010行3列を出発点とすれば乱数列75,38,85,58,…の乱数列を得る。そこで,問の解答として75番,38番,85番の品物を抜き取ればよい。
この例では,100個の品物を母集団としていたが,もし,30個の品物を母集団として3イ固の品物をランダムに抜き取るためには,乱数列75,38, 85, 58, 51,
23, 22, 91,13, 54,24, 25, 58,…の中から3個の乱数列を作ることになるが,母集 団の大きさが30個であるので,これより大きな番号の品物は抜き取ることが
できない。
そこで,その乱数を捨てて,最終的には23番,22番,13番の品物を抜き取ることになる。
このように,乱数を捨てる方法は母集団の大きさが3けた,4けたとなったとき手間がかかり不合理となるので一つの方法として母集団の大きさにより乱数を折り返す方法がある。
たとえば,前記の例のように,母集団の大きさが30個のときは,下図に示すように2けたの乱数を50で折り返して採用する。たとえば,51という乱数を得たときは,1と読み換え,73という乱数を得たときは,23と読み換える。
JIS Z 9031では,このことを“指定された範囲の乱数列に変換する”といって,次のルールを定めている。
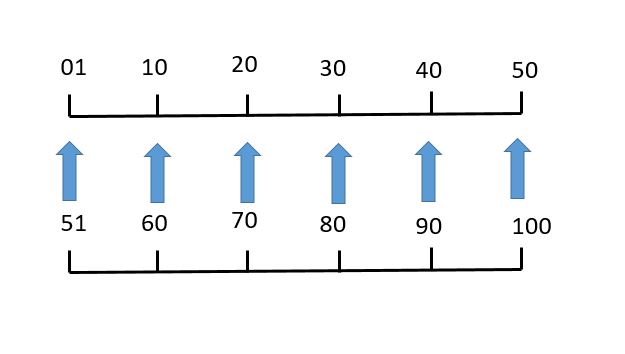
必要な乱数の範囲が1~Nのとき,Nの値により,次のように変換を行う。
(i) N≦10の場合
1けたの原乱数列をとり,yを超えるものはとばして読む、0は10とみなす。
(ii) 11≦N≦20の場合
2けたの原乱数列をとり,20で割った余りで置き換えたのち,yを超えるものはとばして読む、0は20とみなす。
(ⅲ)21≦N≦50の場合
2けたの原乱数列をとり,50で割った余りで置き換えたのち,yを超えるものをとばして読む,0は50とみなす。
(iv) 51≦N≦100の場合
2けたの原乱数列をとり,Nを超えるものをとばして読む.00は100とみなす。
(v) Nが100を超える場合
(i)~(iv)に準じて行う、たとえば, 101≦N≦200ならば3けたの原乱数列をとり,200で割った余りで置き換え, 201≦N≦500ならば500で割って余りで置き換える。
分散の期待値
母集団の平均値μ(母平均)の推定値として,サンプルの平均xを用いると,その分散の期待値は,
$$V(\bar{x})=\frac{N-n}{N-1}\times\frac{\sigma^2}{n}$$
ここに,N:母集団の大きさ
n:サンプルの大きさ
σ2:母集団の分散
となる。
$$\frac{N-n}{N-1}$$
は,有限修正といわれるもので,n/N<0.1の関係にあるときは省略することができる.また,σ2の推定値としては,不偏分散Vで求めることができる。
$$V=\frac{\displaystyle\sum_{i=1}^{n}{(xi-\bar{x})^2}}{n-1}$$
なお,サンプルの試験測定において,個々の測定ごとに$$\sigma{m}^2$$の測定誤差があるときには
$$V(\bar{x})=\frac{\sigma^2}{n}+\frac{\sigma{m}^2}{n}$$
と分散の加法性により$$V(\bar{x})$$を求めることができる。
母集団の総量Xの推定値としてサンプルの$$\bar{x}$$を用いる時の分散の期待値は
$$V({N}\bar{x})=\frac{N-n}{N-1}\times{N}^2\times\frac{\sigma^2}{n}$$
で求められる。
*期待値 expectation:多回数の平均値の分散を計算しその分散の平均値のこと。
単純ランダムサンプリングの設計
次に,単純ランダムサンプリングで得られたデータの平均値の分散の期待値は,
$$V(\bar{x})=\frac{\sigma^2}{n}+\frac{\sigma{m}^2}{n}$$
であるから,目標精度$$V(\bar{x})$$として,母分散を推定することによって上記式よりサンプルの大きさ求めることができる。
単純ランダムサンプリングの場合には,母集団を層別していないのであるから母集団全体の分散を推定することとなる。
*単純サンプリング(単純無作為抽出法)は標本調査の最も基本的な方法ですが、母集団から完全に無作為に調査対象を取り出すのは、非常に手間と時間がかります。
実際の現場では母集団の特徴を反映させつつより手間を軽減させた下記のようなサンプリング方法が使われています。
系統サンプリング
母集団の要素の数は一般に非常に多いので乱数サイを使用した方法はかなり繁雑になり,実用的ではありません。
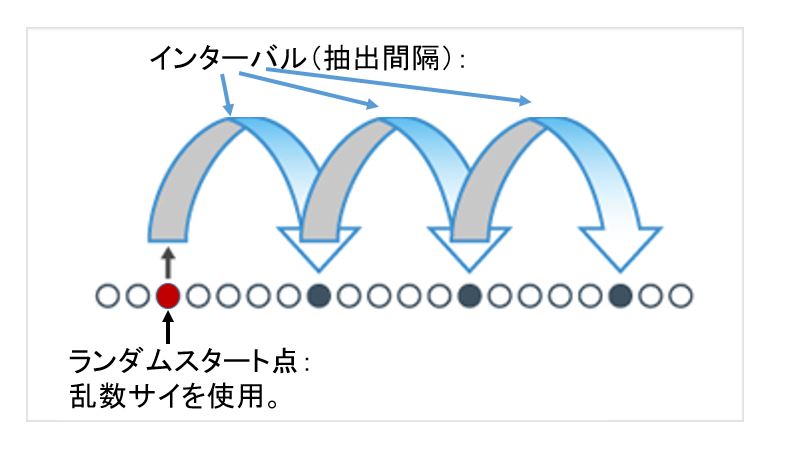
実際に利用されるのは系統サンプリング、抽出法とよばれる無作為抽出法の代用法です。
たとえば45,00個の母集団から10個の標本をとり出す場合, 4500を10で割った450間隔で番号を選ぶわけです。
この抽出間隔は,インターバルとよばれています。この場合にはまず, 001から450までの数字を含む3桁の乱数を1つとり出します。
その乱数が039だったとしたら 0039, 0489, 0939, 1389, 1839, 2289, 2739, 3189 3639, 4089
のような番号が選ばれることになります。
この方法は, 450という等間隔で抽出されるから,一見すると,無作為性が保証されないと感じるかもしれません。
たしかに最初の番号以外は,第1の要素との関係で抽出されますが,標本のメンバーとして選ばれるかどうかは,第1の要素が選出されるまではまったくわかりません。選ばれるときはかたまりとして抽出されますが,第1要素が偶然に選ばれるまでは,どのかたまりも(したがっ
てどの個体も)標本として抽出されるチャンスが等しいということになります。
ただ,注意しなければいけないのは,インターバルの選び方です。つまり,抽出台帳の配列がもっている「周期」 とインターバルとが同調したりすると,ある特定の傾向をもった標本が抽出される危険があるからです。
系統サンプリングの利点は、発生させる乱数が最初のひとつだけでいい点です。母集団において、並び順に意味がある場合、 隣り合わせの順番など近い順番のサンプルが選ばれることがなくなります。
2段サンプリングとは?
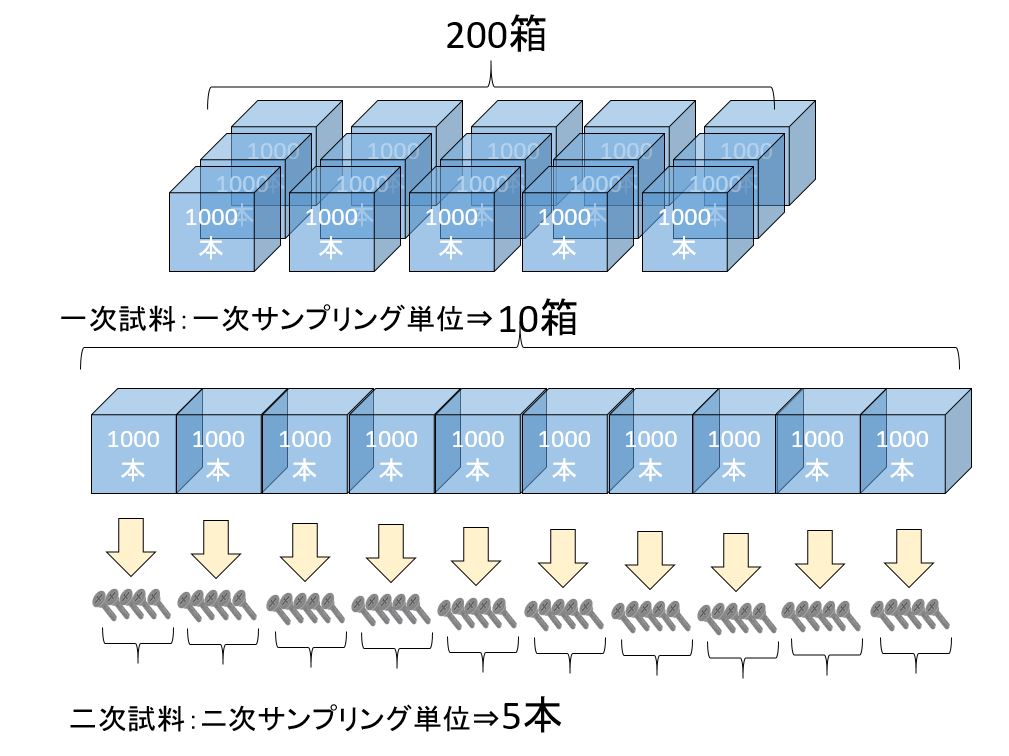
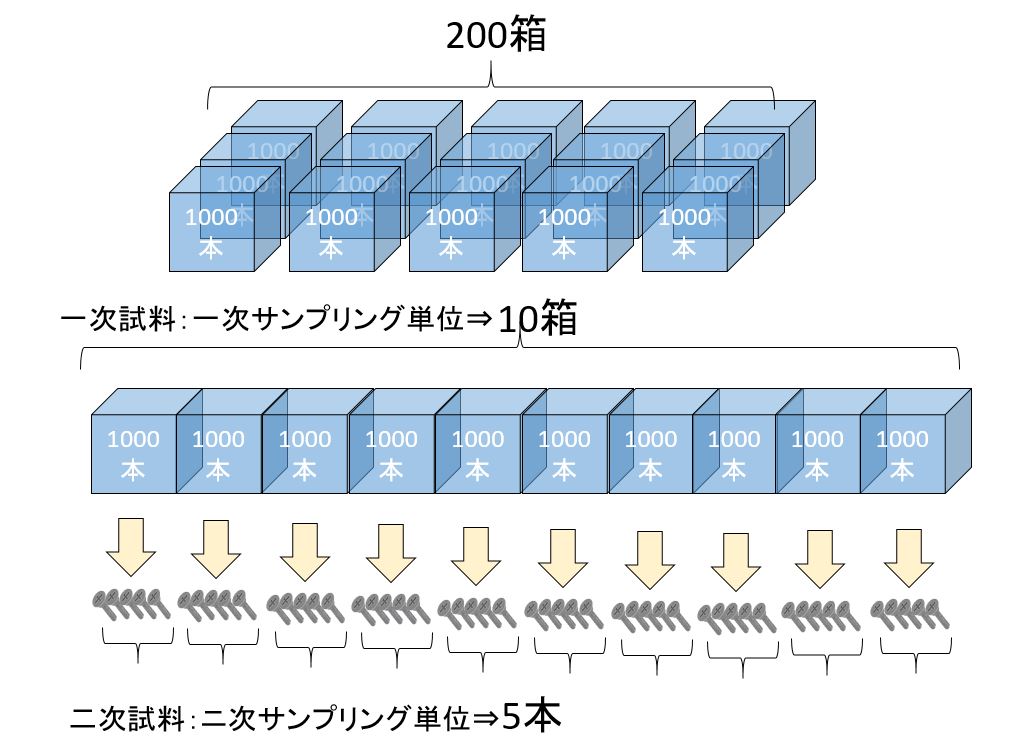
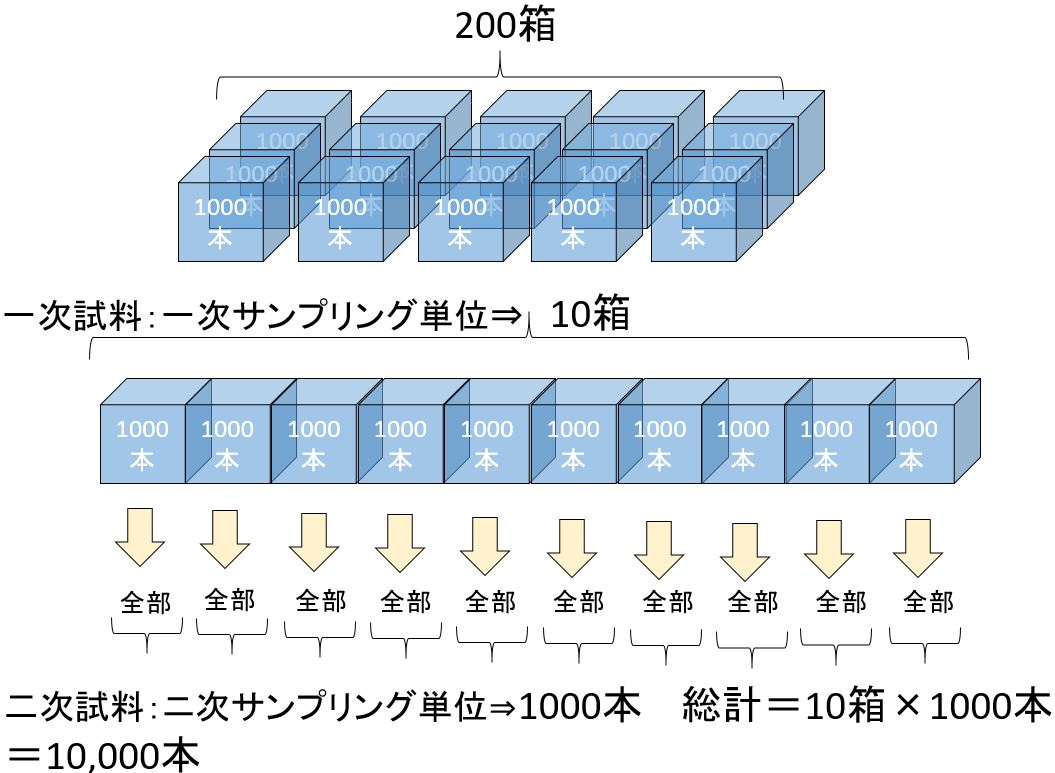
2段サンプリングは,下図に示すように,母集団をいくつかの部分(箱)に分け,その中のいくつかの部分(箱)をランダムにサンプリングし次に抜き取られた箱の中から,おのおのいくつかの単位体(部品)をランダムにサンプリングすることである。
この場合,箱を1次サンプリング単位,部品を2次サンプリング単位といい,また,箱を副ロットという。
工場の場合は,一般に副ロットの大きさ(箱の中の部品数)が一定の場合が多い。
備考:三段以上に分けてサンプリングすることを多段サンプリングという、多段サンプリングの最終段階のサンプルを特に最終サンプルと呼ぶ。
層別サンプリングとは?
層別サンプリングとは「母集団を層別し,各層から一つ以上のサンプリング単位をランダムに取るサンプリング」する事。(Z 8101-2)
事前に各層のサイズの比率がわかっている場合に,その比率に応じて全体のサンプルサイズを各層に割り当てることがある。
このようなサンプリングを層別比例サンプリングという。各層からのサンプリングはランダムに行う。
層別サンプリングは,すべての層からサンプルをとることになる、全層からサンプルを取ることにより,母平均μの推定量の分散には層間分散の項が入らず層内分散の項だけになる。
このため,同一サンプル数を用いる単純ランダムサンプリングに比べて,常に層別サンプリングの方が推定精度がよい。
層別サンプリングは,ロットをいくつかの層に分け,その全部の層からサンプリングする方法であり、これは2段サンプリングにおける1次単位,すなわち副ロットのすべてをサンプリングし,その中から2次単位をサンプリングするものに相当する。
集落サンプリング、クラスターサンプリングとは?
「母集団をいくつかの集落に分割し,全集落からいくつかの集落をランダムに選び,選んだ集落に含まれるサンプリング単位を全て取るサンプリング」
集落は部分母集団の一種で,相互に共通部分を持たず,集落を合わせたものが母集団に一致する.目的とする特性に関して,集落間の差が小さくなるように,集落内のばらつきは大きくなるように集落を設定する」(Z 8101-2)
つまり、集落サンプリングは,ロットをいくつかの層に分け,いくつかの層をランダムサンプリングし,サンプリングされた層の中の全単位について,試験するサンプリングする方法である。これは,2段サンプリングにおける2次単位すなわち、副ロット内の単位体をすべて測定する方法である。
英語では ”cluster sampling”
多段サンプリング、多段抽出法とは?
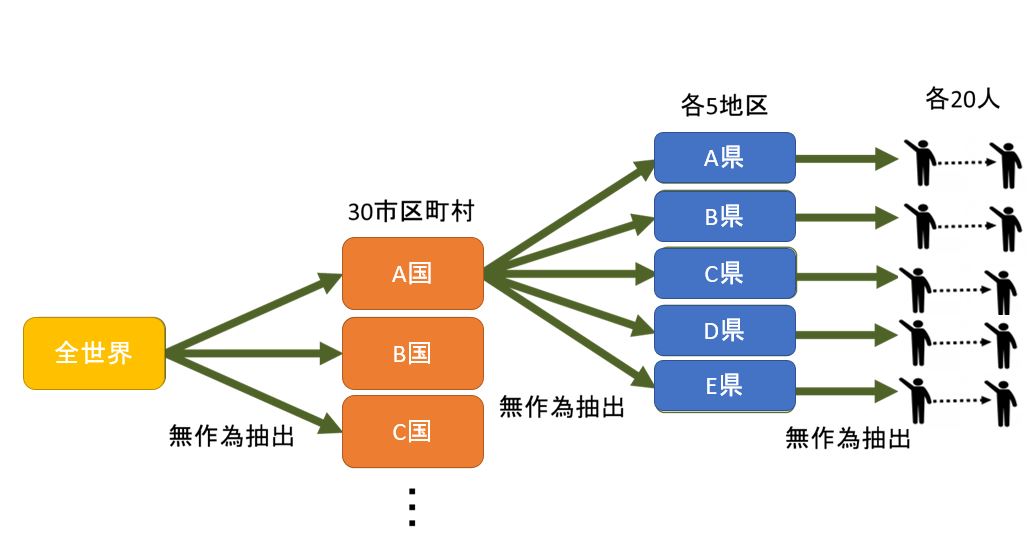
多段サンプリング、多段抽出法は母集団がある程度小さな単位地区に分けられていて,そこから標本を無作為抽出する方法です。
この単位地区は1人ないし数人の調査員があまり移動しなくとも面接ができる程度の大きさでなければなりません。
調査員全体を,まず都市部と群部に比例配分法によって配分します。調査担当者は,さらに調査対象の町や村ごとに配置されます。最後に抽出された町や村で,選挙人名簿などのリストを利用して,実際の被調査者が選ばれることになります。
この調査法では,全ての町や村が調査されるとは限りません。しかし人口数が2倍の町や村には2倍の抽出確率を与えるようにすれば,母集団のどの個体も抽出されるチャンスを等しくすることができるわけです。
未来の統計調査の展望
技術進化による変化
| 項目 | 内容 |
|---|---|
| AI・機械学習 | 膨大なデータをリアルタイムで分析し、より精度の高い推定が可能に。例:SNSから感情傾向を抽出。 |
| IoT・センサー | 人の動きや行動ログをセンサーデータから取得し、自動統計化(例:交通量、購買傾向) |
| ブロックチェーン | 改ざん不可能な集計記録により、統計データの信頼性と透明性が向上。 |
| RPA(自動化) | 調査票の配布・回収・集計作業を自動処理し、人的エラーを削減。 |
調査手法の進化
| 新たな手法 | 内容とメリット |
|---|---|
| パッシブデータ収集 | ユーザーの行動ログや位置情報などを、同意のもとで非介入的に収集。 |
| モバイル調査 | スマホでの常時調査により、若年層や移動層もカバー可能に。 |
| ビッグデータ連携 | 行政データ・企業データ・SNS・購買履歴などを統合分析。 |
| アダプティブ調査 | 回答内容に応じて質問が動的に変化し、負担を減らしつつ精度UP。 |
社会的役割の変化・拡大
| 役割の拡大 | 内容 |
|---|---|
| 災害・感染症対応 | 統計データによりリアルタイムで人流や物資の偏りを把握・対応。例:COVID-19中の人流分析。 |
| 地域格差の可視化 | 小地域単位での統計分析により、ピンポイントな政策立案が可能に。 |
| 市民参加型統計 | 住民が自主的にデータを提供する「参加型センサス」への移行。 |
| エビデンス・ベース政策 | 「感覚」ではなく「データ」による政策意思決定が標準化される。 |
未来の統計調査はどうなるか?
-
✔ リアルタイム化:調査→集計→公開が即時で可能に
-
✔ AIとビッグデータの統合:人間が調査しなくても正確な予測が可能に
-
✔ 信頼性と倫理性の両立:匿名性の確保と信頼性の担保を両立する仕組みが必要
-
✔ 市民参加型へ:自分のデータを社会のために活かすという意識が高まる
まとめ
サンプリングで重要なことは『偏り』に気を付けることです、つまり サンプルとして抽出されたグループが特殊なモノになっていないかということです。
せっかく、事実をベースに論理を組み上げてもその対象となるDataに偏りがあるとその論理の信憑性が崩れます。
具体的には一部の○〇主義の方だけが集めたDataでは信憑性が疑われます。
スライドシェア 統計調査とサンプリング、標本調査
スライドシェアから『統計調査とサンプリング、標本調査』PDF版が無料でダウンロードできます。
参考文献:






























![図解 アンケート調査と統計解析がわかる本[新版]](https://m.media-amazon.com/images/I/51kDYkpJRbL._SL160_.jpg)











コメント